
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблема контроля целостности ядра системы.Содержание книги
Поиск на нашем сайте
Часовым называется любой механизм или процедура, разработанная для снижения воздействия нежелательных событий до того, как они произошли. То есть, часовые являются предупредительным средством в том смысле, что они утанавливаются до того, как происходят события от которых они обеспечивают защиту. Несомненно, что в контексте компьютерных систем проведение защитных действий до причинения какого-либо вреда имеет свои особенности. Некоторые из этих особенностей будут обсуждаться ниже. Интеграция в процессе проектирования. Поскольку часовые должны находится в работоспособном состоянии до возникновения угрозы, то они должны быть идентифицированы и установлены в систему на стадии разработки и проектирования. Системным инженерам гораздо удобнее внести необходимые качества компьютерной системы на ранней стадии разработки, чем добавлять их в готовый проект. Противостояние катастрофическим угрозам. Если определенную угрозу нельзя допустить ни в коем случае (если возможные последствия приведут к гибели большого числа людей), то метод часовых подходит как нельзя лучше, поскольку в такой ситуации принятие защитных действий послe происшедшего нежелательного события является абсолютно недопустимым. Компьютерные системы, управляющие жизненно важными операциями являются наиболее вероятными кандидатами на установку часовых. Возможная растрата ресурсов. Важным аспектом работы часовых, который необходимо принимать во внимание, является оценка дополнительного времени и ресурсов, затрачиваемых на предотвращение событий, которые и так не могут произойти. Например, если наш торговый автомат установлен в менее криминогенном месте (например в монастыре), то часовые будут представлять собой пустую трату ресурсов. Подобно этому, компьютерные системы в некритическом применении могут и не нуждаться в использовании часовых. Сложности в оценке повышения безопасности. Еще одной проблемой при использовании часовых является то, что не всегда можно определить, действительно ли работает часовой. Конечно, это возможно в случаях, когда можно зафиксировать неудачные попытки нападения. Однако в тех случаях, когда нельзя определить, что данный часовой действительно предотвратил потенциальную атаку, оценить достигнутый успех довольно сложно. Можно использовать статистические или вероятностные методы (например использование системы с установленным и неустановленным часовым), но некоторая степень неопределенности будет оставаться. Задачей подсистемы контроля целостности ядра является обеспечение целостности ядра безопасности системы во время ее функционирования и обнаружение некорректного вмешательства субъектов системы в его работу. В основе подсистем контроля целостности системы лежат две основы ные составляющие: статическая (подсистема обеспечена целостности ядра системы) и динамическая (подсистема контроля целостности ядра системы). Рассмотрим эти составляющие подробнее. В основе статической составляющей подсистемы контроля целостности ядра лежит модель целостности информации, например модель Биба. Ядро системы должно находиться на самом привилегированном уровне безопасности в системе и к нему должен быть запрещен доступ по записи со стороны всех менее привилегированных субъектов системы. Реализация подсистемы обеспечения целостности информации должна опираться на аппаратную поддержку вычислительной системы. Подсистема контроля целостности ядра системы. В общем случае, задачей подсистемы контроля целостности системы является динамический анализ целостности ядра системы с целью обнаружения возможных вмешательств в работу ядра системы со стороны менее привилегированных субъектов системы. Подсистема контроля целостности ядра безопасности системы характеризуется двумя параметрами: множество объектов, целостность которых подлежит контролю, и частота срабатывания подсистемы контроля целостности. Рассмотрим влияние данных параметров на безопасность и производительность системы. Допустим ядро синтезированной системы содержит N объектов, из которых М (М≥N), подлежат контролю. При этом безопасность L=M-N объектов не контролируется. При анализе качества синтеза данной системы возможны следующие ситуации; 1. в число L объектов попадают объекты, имеющие непосредственное отношение к реализации правил- ограничений безопасности системы; 2. в число L объектов попадают объекты, не имеющие непосредственного отношения к реализации правил-ограничений безопасности системы; 3. в число L объектов попадают объекты, не имеющие непосредственного отношения к реализации правил-ограничений безопасности системы, но при нарушении целостности которых можно воздействовать на объекты, имеющие отношение к реализации правил-ограничений системы безопасности. Рассмотрим все эти ситуации. Ситуация 1 показывает отсутствие контроля целостности объекта, принадлежащего ядру безопасности со стороны системы. Нарушение целостности данного объекта останется незамеченным системой в процессе ее функционирования, что может привести к нарушению безопасности системы. Ситуация 2 показывает нарушение целостности объекта системы, не приводящее к нарушению ее безопасности. Хотя нарушение целостности данного объекта останется незамеченным системой в процессе ее функционирования, нарушения безопасности системы не произойдет. Ситуация 3 показывает случай, при котором нарушение целостности объекта не приводит непосредственно к нарушению безопасности системы, но может привести к нарушению целостности системы и привести к ситуации 1. Влияние множества контролируемых объектов системы на ее производительность можно выразить следующим выражением. Допустим в цикле Т проверяется целостность М объектов. Для "miÎM существует параметр ti, определяющий время, затрачиваемое системой на проверку целостности объекта mi. Параметр ti определяет сложность алгоритма проверки целостности объекта системы mi и может выражаться в количестве тактов, в течении которых процессор проверяет целостность объекта mi. При увеличении значения данного параметра с одной стороны возрастает надежность контроля целостности объекта mi, а с другой — возрастает время, затрачиваемое на контроль целостности системы, и как следствие падает ее производительность. Тогда однократная проверка системой целостности объектов ядра займет время: T1= Частота срабатывания подсистемы контроля целостности ядра определяет время, которое система будет находиться в состоянии "утечки информации" в случае нарушения целостности системы. Иными словами, если подсистема контроля целостности отрабатывает один раз за временной промежуток Т, то система, при условии нарушения целостности ядра, система будет находиться в состоянии утечки информации в течение временного промежутка [0,Т]. К определению интервала времени Т возможно два подхода. Первый подход характерен минимизацией потери производительности системы вследствие наличия в системе подсистемы контроля целостности ядра. При этом подсистема контроля целостности ядра срабатывает в том случае, если субъекты системы не используют процессорное время в течение промежутка времени Т. При этом частота срабатывания подсистемы контроля целостности ядра нерегулярна, так как она имеет низкий приоритет по сравнению с остальными субъектами системы, но при этом не происходит потери производительности системы. Второй подход характерен тем, что он обеспечивает более высокий уровень безопасности при возможных потерях производительности системы. В данной ситуации подсистема контроля целостности ядра имеет высокий приоритет и срабатывает независимо от условий функционирования системы один раз за период времени Т. Нижней границей определяющей значение Т, является выражение, определяющее максимально возможное время, которое система может провести в состоянии утечки информации. Это время определяется, исходя из вероятности преодоления подсистемы контроля целостности. Будем считать подсистему контроля целостности нарушенной в том случае, когда субъект нарушитель смог изменить алгоритм подсистемы контроля целостности. Для этого ему необходимо преодолеть подсистему обеспечения целостности. Таким образом, для стопроцентного детектирования появления канала утечки информации, возникающего вследствие нарушения целостности системы необходимо, чтобы подсистема контроля целостности срабатывала за период времени, не превышающий минимальное время, необходимое для преодоления субъектом-нарушителем подсистемы обеспечения целостности и модификации подсистемы контроля целостности. Для определения времени, необходимого для изменения алгоритма контроля целостности необходимо для синтезированной системы контроля и обеспечения целостности построить граф, отражающий все возможные пути преодоления подсистемы обеспечения целостности и модификации подсистемы контроля целостности. Пример данного графа приведен на рисунке 2.2. Узлами данного графа являются компоненты подсистемы обеспечения целостности. Конечной вершиной каждого пути на данном графе является подсистема контроля целостности. Характеристикой каждого узла графа является время, необходимое для преодоления данного компонента подсистемы обеспечения целостности, а также вероятность преодоления данного компонента, в предположении, что предыдущий компонент данного пути преодолен. Для первого элемента каждого пути данная вероятность полагается равной единице. Тогда, нижнюю границу периода срабатывания подсистемы контроля целостности информации можно записать как: Т2≤ min (Тp1, Тp2,... Тpn) (2) где Т — время преодоления системы соответствующее пути m на графе; Тpm = где Tpim- время преодоления подсистемы i принадлежащей пути m; Pi,i–1 — вероятность преодоления подсистемы i при условии преодоления подсистемы i-1. Для первого элемента в пути, ведущем к преодолению подсистемы контроля целостности, Р=1. То есть предполагается, что данное звено в системе некорректно. При выполнении условия, определенного в (2), субъекту-злоумышленнику преодолеть подсистему контроля целостности не удастся. На рисунке 1 показаны возможные пути нарушения подсистемы целостности информации. На данном рисунке ПКЦ — подсистема контроля целостности, а Тркпц — время разрушения подсистемы контроля целостности.
рисунок 2.2. На данном рисунке показано два пути нарушения подсистемы контроля целостности. Для пути 1 суммарное время нарушения подсистемы контроля целостности. Тнар1=Тр1+ТрЗ+Трпкц. Для пути 2 суммарное время нарушения подсистемы контроля целостности Тнар1=Тр2+Трn+Трпкц. Таким образом, период функционирования подсистемы контроля целостности должен быть: Т ≤min(Тнар.1, Тнар.2) Выражение (2) определяет нижнюю границу возможного значения периода функционирования подсистемы контроля целостности. Верхняя граница значения периода функционирования подсистемы контроля целостности определяется исходя из возможной потери производительности системы. При этом потеря производительности системы с учетом множества контролируемых объектов определяется как: Р=(Т4-Т1)/Т4= 1 - Где показатель t/T отражает отношение сложности кoнтроля проверки целостности объекта ядра системы oтнocительно частоты срабатывания подсистемы защиты информации. Из данного выражения видно, что если задано значение, определяющее допустимую потерю производительности системы Р и заданы алгоритмы контроля целостности ядра системы ti, то можно вычислить интервал времени Т, в течении которого должна срабатывать система контроля целостности. Очевидно, что с целью повышения производительности системы должно выполняться выражение Т→mах, т.е. чем реже выполняется контроль целостности ядра системы, тем меньше потеря производительности. Из данного выражения может быть вычислена верхняя граница времени Т-периода срабатывания подсистемы контроля целостности информации: T5 ≥ Таким образом, исходя из выражений (2) и (5) может быть выбран период срабатывания подсистемы контроля целостности для второго подхода. Если значение, полученное из (2) больше, чем значение, полученное из (5), то нам удалось спроектировать систему с заданной потерей производительности и с гарантией контроля целостности. Если значение, полученное из (2) меньше или равно, значению, полученному из (5), то нам удалось спроектировать систему с заданной потерей производительности и с вероятностью того, что подсистема контроля целостности не будет преодолена с вероятностью: Р = (Т5 - Т2) / Т5 (6) где Т5 — период срабатывания подсистемы контроля целостности, вычисленный исходя из уравнения (5). Т2 — период срабатывания подсистемы контроля целостности, вычисленный исходя из уравнения (2). В случае, если Т2>Т5, для достижения приемлемых безопасности и потери производительности, необходимо изменить алгоритмы контроля целостности системы.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.108.174 (0.008 с.) |

 (1)
(1) Tpim / P i,i – 1 (3)
Tpim / P i,i – 1 (3)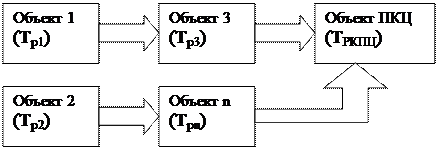
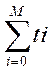 /T4 (4)
/T4 (4) /(P-1) (5)
/(P-1) (5)


