Использование понятия легитимности при построении модели безопасности ВС.

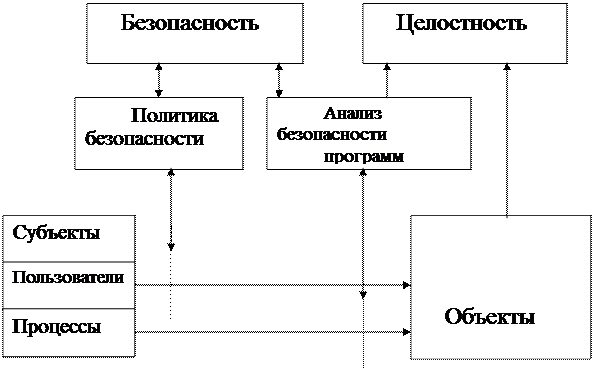
Введенные понятия позволяют перейти к построению модели безопасности ВС, базирующейся на понятии легитимного и нелегитимного доступа. Данная модель служит развитием известных моделей безопасности [7], использующих понятия санкционированного и несанкционированного доступа, является их логическим следствием и модернизирует их с учетом действия РПС и современной парадигмы функционирования ВС.

Будем рассматривать ВС как совокупность двух множеств — множества объектов О и множества субъектов S. Объекты представляют собой пассивные компоненты ВС и описываются рассмотренной объектно-концептуальной моделью. Субъекты являются активными компонентами и устанавливают различные отношения с объектами Множество субъектов S состоит из двух подмножеств — пользователей (S_u) и процессов (S_p). Процессы представляют собой выполняющиеся программы, действующие от имени пользователей, или от своего собственного. Процесс представляет собой реализацию последовательности отношений между субъектами и объектами, принадлежащих полному множеству отношений R=S*O. Тип отношений зависит от типа объекта (чтение, запись, использование, запуск и т.д.). Как уже говорилось отношения делятся на легитимные и нелегитимные.

Для оценки состояния ВС предлагается использовать две характеристики — безопасность и целостность Исходя из определения понятия легитимности очевидно, что безопасность и целостность системы определяются легитимностью отношений, установленных между составляющими ее субъектами и объектами. Очевидно, что такая проверка должна производится перед установлением отношений и предотвращать попытки установить нелегитимные отношения. В том случае, когда субъектом является пользователь, отношения пользователь—объект контролируются политике безопасности, принятой в ВС. Если субъектом является процесс, то проверка легитимности отношений процесс-объект составляет задачу анализа безопасности программ. На рис.2.5. показана схема контроля легитимности отношений в ВС

 

 

 

 

 

 

Рис. 2.5. Схема контроля легитимности отношений в ВС.

 

Это позволяет сформулировать следующий критерий безопасности систем, являющийся развитием основной теоремы безопасности:

Система состоящая из множества объектов О и субъектов S является безопасной и целостной на шаге n, если все существовавшие в ней до этого шага отношения между субъектами и объектами были легитимны, т.е. R_iÎL для всех i<n.

Методы и средства контроля отношений пользователь-объект в соответствии с той или иной политикой безопасности были исследованы в многочисленных работах, посвященных моделям безопасности[8,9,10,11], включены в стандарты на защищенные ВС и ОС и нашли свое воплощение во многих защищенных ОС.

Для решения задачи проверки легитимности отношений vежду процессами и объектами ВС предлагается использовать развиваемый в данной работе подход к анализу безопасности программ, формальная постановка которого будет рассмотрена далее.

Пространство программ.

Обозначим через Ƥ множество всех возможных для данной ВС программ, или пространство программ, очевидно что РÎƤ. Обозначим через V множество всех РПС, VÎƤ. Отметим, что любая программа, обладающая свойствами РПС, должна быть отнесена к РПС — например, любая прикладная программа, зараженная вирусом или содержащая в себе троянского коня, принадлежит множеству РПС.

Теоретическим исследованием множества РПС V занимались многие авторы, в т.ч. Адлеман[4], Доулинг[12], Коэн[13]. Эти работы показали, что исследования РПС и способов их обнаружения пересекаются с задачами доказательства полноты множеств и проблемой вычислимости.

На данный момент одним из основных результатов исследований в этой области стало доказательство Адлеманом[4] полноты множества V, хотя использованный метод доказательства не позволяет эффективно построить процедуру порождения этого множества. Множество называется полным, если оно перечислимо и к нему сводится любое другое перечислимое множество [14]. Сводимость одного множества к другому (сводимость по Тьюрингу) означает, что существует характеристическая функция одного множества относительно другого. Из полноты множества V следует его перечислимость, что означает, что оно является областью значений некоторой общерекурсивной функции, т. е. существует общерекурсивная функция j_v(х), такая, что vÎV, если и только если существует такой х, что v=j_v(х). В принципе этот результат устанавливает возможность создания процедуры, порождающей множество программ, являющихся РПС.

Для полного решения проблемы безопасности программ необходимо доказать утверждение о разрешимости множества V. Для этого необходимо доказать, что существует разрешающий алгоритм D_v который для любой программы р дает ответ, принадлежит р множеству V или нет. На сегодняшний день разрешимость множества V формально не доказана. В работе Ф.Коэна[13] имеются рассуждения о невозможности построения универсального распознавателя РПС, однако они носят неформальный характер и не являются окончательными. Решения вопроса, связанные с доказательством разрешимости некоторых подмножеств множества V будут обсуждаться далее при рассмотрении различных методов анализа безопасности.