
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика решения задач ЛП графическим методомСтр 1 из 3Следующая ⇒
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ Теоретическое введение Графический метод довольно прост и нагляден для решения задач ЛП с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи. Каждое из неравенств задачи ЛП (1.1) определяет на координатной плоскости Примечание №2.1. Все вышесказанное относится и к случаю, когда система ограничений (1.1) включает равенства, поскольку любое равенство
можно представить в виде системы двух неравенств (см. рис.2.1)
ЦФ Это связано с тем, что изменение значения L повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси Вектор Суть графического метода заключается в следующем. По направлению (против направления) вектора
При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.
Задача Найдем оптимальное решение задачи №1.01 о красках, математическая модель которой имеет вид
Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат (рис.2.2).
(1) – Прямая (4) проходит через точку
Рис.2.2. Графическое решение задачи №2.01
Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (3), получим Целевую прямую можно построить по уравнению
Строим вектор
Максимальное значение ЦФ равно Задача №2.02
Построим ограничения (рис.2.3). (1) – (4) –
Целевую прямую построим по уравнению
Определим ОДР. Ограничение-равенство (4) допускает только точки, лежащие на прямой (4). Подставим точку (0;0) в ограничение (3), получим
Строим вектор Определим координаты точки В из системы уравнений прямых ограничений (3) и (4)
Минимальное значение ЦФ равно
При поиске точки максимума ЦФ будем двигать целевую прямую по направлению вектора
Максимальное значение ЦФ равно
Таким образом, В(3,46; 1,85) – точка минимума,
Задача №2.03
Построим ограничения (рис.2.4) (1) – Прямая (3) – проходит через точку Целевую прямую построим по уравнению
Определим ОДР. Подставим точку (0;0) в ограничение (2), получим
Рис.2.4. Графическое решение задачи №2.03
Аналогично определим и укажем допустимые полуплоскости для остальных ограничений (см. рис.2.4). Анализ допустимых полуплоскостей позволяет определить, что ОДР – это незамкнутая область, ограниченная прямыми (2), (3), (4) и осью Строим вектор При поиске максимума ЦФ будем двигать целевую прямую по направлению вектора
Максимальное значение ЦФ равно
Таким образом, в данной задаче ЦФ не ограничена на множестве планов снизу, а А(1;4) является точкой максимума ЦФ,
Теоретическое введение Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП. Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограничения проходят черезоптимальную точку. Несвязывающие ограничения не проходят черезоптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением – недефицитным. Ограничениеназывают избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.
1. Анализ сокращения или увеличения ресурсов: · на сколько можно увеличить (ограничения типа · на сколько можно уменьшить (ограничения типа 2. Увеличение (ограничения типа 3. Анализ изменения коэффициентов ЦФ: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение? Правило №3.3 Чтобы определить максимальное уменьшение запаса недефицитного ресурса, не меняющее оптимальное решение, необходимо передвигать соответствующую прямую до пересечения с оптимальной точкой. Правило №3.4 Чтобы численно определить минимальную величину запаса недефицитного ресурса, не меняющую оптимальное решение, необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения. Чтобы выяснить, до каких пределов падение спроса на краску 2-го вида не повлияет на производство в точке
Делаем вывод: предельный уровень, до которого может упасть спрос на краску 2-го вида и при котором не изменится оптимальность полученного ранее решения, равен
Экономический смысл ограничения (3)
в том, что объем продаж краски 2-го вида может превысить объем продаж краски 1-го вида максимум на 1 т. Дальнейшее увеличение продаж краски 2-го вида по сравнению с краской 1-го вида графически отобразится перемещением прямой (3) влево и вверх, но никак не повлияет на оптимальность точки Е. Но если разность спросов на краску 2-го и 1-го видов будет уменьшаться, то прямая (3) будет перемещаться ниже и правее. Последним положением прямой (3), при котором точка Е остается оптимальной, является пересечение с точкой Е (см. рис.3.1). Согласно правилу №3.4, подставим координаты точки
Получаем, что разность спросов на краску 2-го и 1-го вида в точке стала отрицательной. То есть, прохождение прямой (3) через точку Е означает, что краску 2-го вида будут покупать в меньшем объеме, чем краску 1-го вида
Делаем вывод: максимальное превышение спроса на краску 1-го вида над спросом на краску 2-го вида, при котором оптимальное решение в точке Е не изменится, составляет 2 т краски в сутки. Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл.3.1. Таблица 3.1 Правило №3.5 Чтобы определить границы допустимого диапазона изменения коэффициента ЦФ, например необходимо приравнять тангенс угла наклона целевой прямой
Рис.3.5. Определение
Рис.3.6. Определение Определим насколько максимально может снизиться цена на краску 1-го вида, не изменяя оптимальную точку Е. Для этого применим правило №3.5 и формулу расчета тангенса угла наклона прямой (рис.3.7).
Рис.3.7. Определение тангенса угла наклона Определим тангенсы углов наклона: 1) целевой прямой
2) связывающего ограничения
3) связывающего ограничения
Для нахождения min
Для нахождения max
Таким образом, если цены на краску первого вида будут колебаться в пределах Из приведенных выше расчетов и графической их иллюстрации следует, что если цена на краску первого вида станет меньше 1 тыс.руб./т (
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ Теоретическое введение Графический метод довольно прост и нагляден для решения задач ЛП с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи. Каждое из неравенств задачи ЛП (1.1) определяет на координатной плоскости
Примечание №2.1. Все вышесказанное относится и к случаю, когда система ограничений (1.1) включает равенства, поскольку любое равенство
можно представить в виде системы двух неравенств (см. рис.2.1)
ЦФ Это связано с тем, что изменение значения L повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси Вектор Суть графического метода заключается в следующем. По направлению (против направления) вектора При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.
Методика решения задач ЛП графическим методом I. В ограничениях задачи (1.1) замените знаки неравенств на знаки точных равенств и постройте соответствующие прямые. II. Найдите и заштрихуйте полуплоскости, разрешенные каждым из ограничений-неравенств задачи (1.1). Для этого подставьте в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверьте истинность полученного неравенства. Если неравенство истинное, то надо заштриховать полуплоскость, содержащую данную точку; иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку. Поскольку Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому выделите на графике такие прямые. III. Определите ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделите ее. При отсутствии ОДР задача не имеет решений, о чем сделайте соответствующий вывод. IV. Если ОДР – не пустое множество, то постройте целевую прямую, т.е. любую из линий уровня V. Постройте вектор VI. При поиске max ЦФ передвигайте целевую прямую в направлении вектора VII. Определите координаты точки max (min) ЦФ Задача Найдем оптимальное решение задачи №1.01 о красках, математическая модель которой имеет вид
Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат (рис.2.2).
(1) – Прямая (4) проходит через точку
Рис.2.2. Графическое решение задачи №2.01
Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (3), получим Целевую прямую можно построить по уравнению
Строим вектор
Максимальное значение ЦФ равно Задача №2.02
Построим ограничения (рис.2.3). (1) – (4) –
Целевую прямую построим по уравнению
Определим ОДР. Ограничение-равенство (4) допускает только точки, лежащие на прямой (4). Подставим точку (0;0) в ограничение (3), получим Строим вектор Определим координаты точки В из системы уравнений прямых ограничений (3) и (4)
Минимальное значение ЦФ равно
При поиске точки максимума ЦФ будем двигать целевую прямую по направлению вектора
Максимальное значение ЦФ равно
Таким образом, В(3,46; 1,85) – точка минимума,
Задача №2.03
Построим ограничения (рис.2.4) (1) – Прямая (3) – проходит через точку Целевую прямую построим по уравнению
Определим ОДР. Подставим точку (0;0) в ограничение (2), получим
Рис.2.4. Графическое решение задачи №2.03
Аналогично определим и укажем допустимые полуплоскости для остальных ограничений (см. рис.2.4). Анализ допустимых полуплоскостей позволяет определить, что ОДР – это незамкнутая область, ограниченная прямыми (2), (3), (4) и осью Строим вектор При поиске максимума ЦФ будем двигать целевую прямую по направлению вектора
Максимальное значение ЦФ равно
Таким образом, в данной задаче ЦФ не ограничена на множестве планов снизу, а А(1;4) является точкой максимума ЦФ,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.119.219 (0.162 с.) |
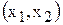 некоторую полуплоскость (рис.2.1), а система неравенств в целом – пересечение соотвествующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи (1.1) ОДР является пустым множеством.
некоторую полуплоскость (рис.2.1), а система неравенств в целом – пересечение соотвествующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи (1.1) ОДР является пустым множеством.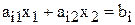
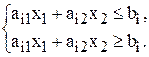
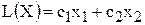 при фиксированном значении
при фиксированном значении  определяет на плоскости прямую линию
определяет на плоскости прямую линию  . Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.
. Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.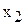 (начальная ордината), а угловой коэффициент прямой
(начальная ордината), а угловой коэффициент прямой 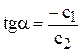 останется постоянным (см. рис.2.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.
останется постоянным (см. рис.2.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.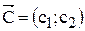 с координатами из коэффициентов ЦФ при
с координатами из коэффициентов ЦФ при  и
и 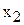 перпендикулярен к каждой из линий уровня (см. рис.2.1). Направление вектора
перпендикулярен к каждой из линий уровня (см. рис.2.1). Направление вектора 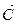 совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположнонаправлению вектора
совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположнонаправлению вектора 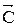 в ОДР производится поиск оптимальной точки
в ОДР производится поиск оптимальной точки  . Оптимальной считается точка, через которую проходит линия уровня
. Оптимальной считается точка, через которую проходит линия уровня 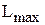 (
(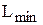 ), соответствующая наибольшему (наименьшему) значению функции
), соответствующая наибольшему (наименьшему) значению функции 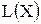 . Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.
. Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.
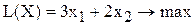
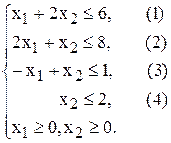
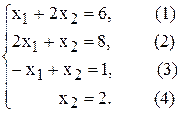
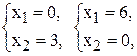 (2) –
(2) – 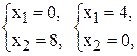 (3) –
(3) – 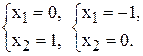
 параллельно оси
параллельно оси  .
.
 , что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис.2.2). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник ABCDEF.
, что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис.2.2). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник ABCDEF.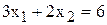 ,
,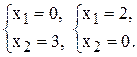
 из точки (0;0) в точку (3;2). Точка Е – это последняя вершина многоугольника допустимых решений ABCDEF, через которую проходит целевая прямая, двигаясь по направлению вектора
из точки (0;0) в точку (3;2). Точка Е – это последняя вершина многоугольника допустимых решений ABCDEF, через которую проходит целевая прямая, двигаясь по направлению вектора 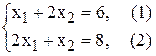
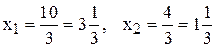 ,
, [т/сутки].
[т/сутки]. [тыс. руб./сутки]. Таким образом, наилучшим режимом работы фирмы является ежесуточное производство краски 1-го вида в объеме
[тыс. руб./сутки]. Таким образом, наилучшим режимом работы фирмы является ежесуточное производство краски 1-го вида в объеме 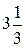 т и краски 2-го вида в объеме
т и краски 2-го вида в объеме 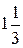 т. Доход от продажи красок составит
т. Доход от продажи красок составит 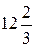 тыс. руб. в сутки.
тыс. руб. в сутки.
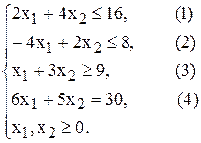
 (2) –
(2) – 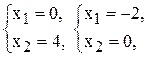 (3) –
(3) – 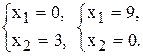


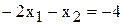 ,
,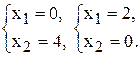
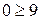 , что является ложным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, не содержащую точку (0;0), т.е. расположенную выше прямой (3). Аналогично определим и укажем допустимые полуплоскости для остальных ограничений (см. рис.2.3). Анализ полуплоскостей, допустимых остальными ограничениями-неравенствами, позволяет определить, что ОДР – это отрезок АВ.
, что является ложным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, не содержащую точку (0;0), т.е. расположенную выше прямой (3). Аналогично определим и укажем допустимые полуплоскости для остальных ограничений (см. рис.2.3). Анализ полуплоскостей, допустимых остальными ограничениями-неравенствами, позволяет определить, что ОДР – это отрезок АВ.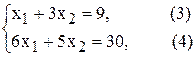
 .
.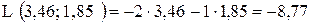 .
.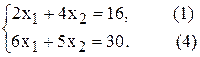
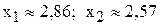 .
. .
.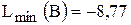 ;
;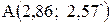 – точка максимума,
– точка максимума, 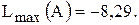
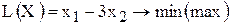
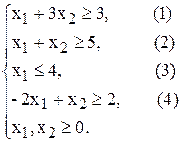
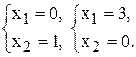 (2) –
(2) – 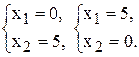 (4) –
(4) – 
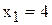 параллельно оси
параллельно оси 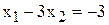 ,
,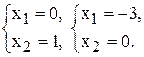
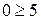 , что является ложным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, не содержащую точку (0;0), т.е. расположенную правее и выше прямой (2).
, что является ложным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, не содержащую точку (0;0), т.е. расположенную правее и выше прямой (2).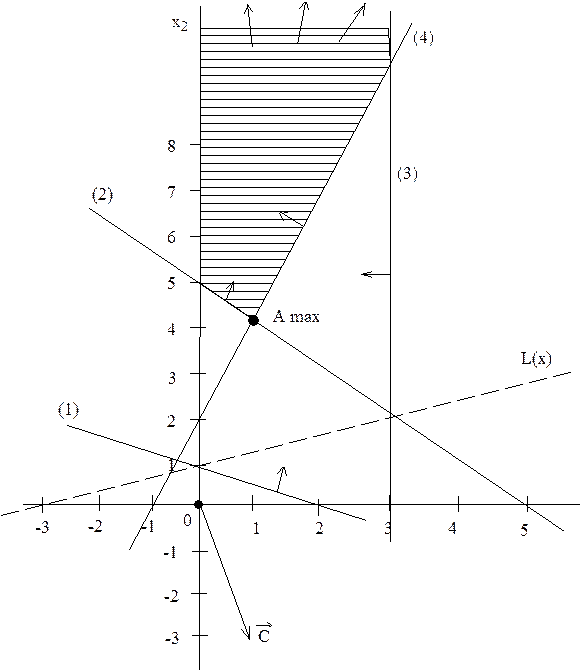
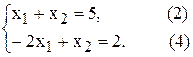
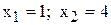 .
.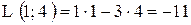 .
.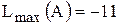 .
.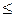 ) запас дефицитного ресурса для улучшения оптимального значения ЦФ?
) запас дефицитного ресурса для улучшения оптимального значения ЦФ?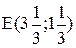 , используем правило №3.4. Подставляем в левую часть ограничения (4) координаты точки Е, получаем
, используем правило №3.4. Подставляем в левую часть ограничения (4) координаты точки Е, получаем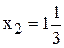 .
.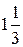 т краски в сутки.
т краски в сутки.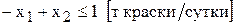
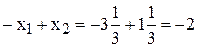 [т краски].
[т краски].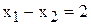 [т краски/сутки].
[т краски/сутки]. и
и 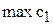 ,
, поочередно к тангенсам углов наклона прямых связывающих ограничений, например
поочередно к тангенсам углов наклона прямых связывающих ограничений, например  и
и  (рис.3.5 и 3.6).
(рис.3.5 и 3.6).
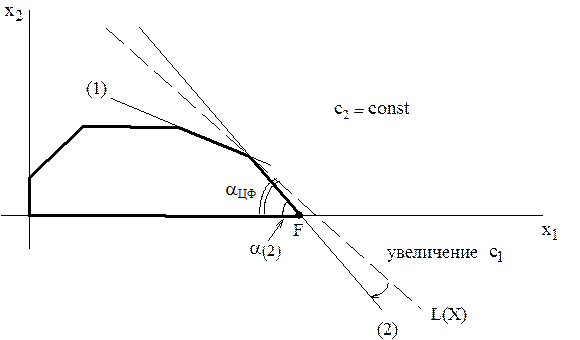

 прямой
прямой 
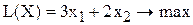 , учитывая, что
, учитывая, что  фиксировано
фиксировано ;
; (1)
(1) ;
;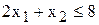 (2)
(2) .
. целевая прямая должна совпасть с прямой (1) (см. рис.3.5):
целевая прямая должна совпасть с прямой (1) (см. рис.3.5): ;
; ;
; [тыс.руб./т].
[тыс.руб./т]. ;
; ;
;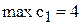 [тыс.руб./т].
[тыс.руб./т]. тыс. руб./т, то оптимальное решение задачи не изменится.
тыс. руб./т, то оптимальное решение задачи не изменится. ), то наиболее выгодным будет производство красок в точке D (см. рис.3.5). При этом общее потребление ингредиента В снизится, что приведет к его недефицитности [ресурс (2)], а дефицитными будут ресурсы (1) и (4).
), то наиболее выгодным будет производство красок в точке D (см. рис.3.5). При этом общее потребление ингредиента В снизится, что приведет к его недефицитности [ресурс (2)], а дефицитными будут ресурсы (1) и (4).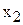 должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси
должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси  , т.е. удобное для проведения расчетов. Способ построения аналогичен построению прямых ограничений.
, т.е. удобное для проведения расчетов. Способ построения аналогичен построению прямых ограничений.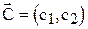 , который начинается в точке (0;0), заканчивается в точке
, который начинается в точке (0;0), заканчивается в точке 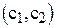 . Если целевая прямая и вектор
. Если целевая прямая и вектор 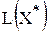 . Для вычисления координат оптимальной точки
. Для вычисления координат оптимальной точки 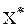 решите систему уравнений прямых, на пересечении которых находится
решите систему уравнений прямых, на пересечении которых находится 


