
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вырожденные случаи линий 2-го порядка.Содержание книги
Поиск на нашем сайте Вырожденные случаи поверхностей 2-го порядка. Графики в полярной системе координат и параметрически заданных функций. Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами. Способ задания начальных условий для решения какой – либо конкретной технической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат. Полярная система координат. Точка О называется полюсом, а луч l – полярной осью.
Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох. Действительные числа. Действительные числа образуют совокупность элементов, обладающую следующими свойствами. Если a и b - действительные числа (алгебраические, рациональные, целые, положительные целые), то таковыми же являются и 1. a + b и ab (замкнутость), 2. a + b = b + a, ab = ba (коммутативность), 3. a + (b + c) = (a + b) + c = a + b + c, a(bc) = (ab)c = abc (ассоциативность 4. a * 1 = a (единица), 5. a(b + c) = ab + ac (дистрибутивность), 6. из a + c = b + c следует a = b, из ca = cb,, следует a = b (сокращение).
Действительное число 0 (нуль) обладает свойствами a + 0 = a, a * 0 = 0 для каждого действительного числа a.
Действительные числа, не являющиеся рациональными, называются иррациональными. Действительными алгебраическими числами называются действительные корни алгебраических уравнений с целочисленными коэффициентами, а действительными трансцендентными числами - остальные действительные числа. Множества и операции над ними. Множества – совокупность некоторых объектов, объединенных по какому-то признаку. Объекты из которых состоит множество, называются элементами. Множества принято обозначать заглавными латинскими буквами А,B,C…,а их элементы - малыми буквами. Множество, не содержащее ни одного элемента, называется пустым множеством. Элементы множества записывают в фигурных скобках, внутри которых они перечислены. Множество А называется подмножеством В, если каждый элемент множества А является элементом множества В. Множества А и В равны или совпадают, если они состоят из одних и тех же элемнтов. Объединение – множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Пересечение – множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Множества, элементами которых являются числа, называются числовыми.
Множество К содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Предел последовательности. Число а называется пределом последовательности, если для любого положительного числа Е найдется такое натуральное число N, что при всех n>N выполняется равенство:
Коротко определение предела: Сходящаяся последовательность имеет только один предел. Последовательность, неимеющая предела, называется расходящейся. Если Если
Теорема 1: (необходимый признак числовой последовательности): если последовательность сходится, то она ограничена., если последовательность неограниченна, то она расходится. Теорема Вейерштрасса: сформируем достаточный признак числовой последовательности: всякая ограниченная монотонная последовательность имеет предел. Теорема: если две последовательности {xn}и {yn} сходятся, т.е. имеют конечные пределы, то сходятся также сумма, разность, произведение, частное этих последовательностей, т.е.: Теорема: если Доказательство:
Предел функции. Сформулируем два, эквивалентных между собой, определения предела функции в точке: Определение (по Коши): число А называется пределом функции в точке х0, если для любого положительного Коротко это определение:
Определение (по Гейне): Число А называется пределом функции Односторонние пределы: Предел слева записывают так: Аналогично определяется предел функции справа:
Пределы функции слева и справа называются односторонними пределами. Предел функции при Число А называется пределом функции при
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.005 с.) |



 . В этом случае пишут
. В этом случае пишут 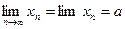 и говорят, что последовательность {xn}имеет предел, равный числу а. говорят,что последовательность сходится к а.
и говорят, что последовательность {xn}имеет предел, равный числу а. говорят,что последовательность сходится к а. .
. =0 => последовательность бесконечно малая.
=0 => последовательность бесконечно малая. => бесконечно большая.
=> бесконечно большая. =>
=>  .
. - окрестности точки а.
- окрестности точки а.  =>
=>  и тд.
и тд. и начиная с некоторого номера выполняется неравенство xn
и начиная с некоторого номера выполняется неравенство xn  yn, то а
yn, то а  >0 найдется такое натуральное число N(
>0 найдется такое натуральное число N( т.е.
т.е. . Возьмем
. Возьмем  . Тогда:
. Тогда:  отсюда следует, что xn>yn, это противоречит условию xn
отсюда следует, что xn>yn, это противоречит условию xn 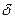 , что для всех х
, что для всех х  х0, удовлетворяющих неравенству
х0, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
. .
. в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции
в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции  ,
,  , сходится к числу А.
, сходится к числу А. >0 существует число
>0 существует число  выполняется неравенство
выполняется неравенство  .
.
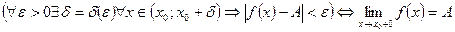 .
.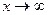 :
: выполняется неравенство
выполняется неравенство 



