
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вихідні дані для курсової роботи представлені у вигляді двох десяткових чисел А(10) і В(10).Содержание книги
Поиск на нашем сайте
Номер завдання – 41
2.1.1. Перевести числа А(10) і В(10) в двійкову систему числення по загальному правилу переводу, а також через вісімкову систему числення. По загальному правилу переводу: а) А10 " А2;
А2=100001001;
б) В10 " В2;
В2=1000001111; Через вісімкову систему числення: а) А10 " А8" А2;
А8=411 А2=100001001 б) В10 " В8" В2;
В8=1017 В2=1000001111 2.1.2. Записати десяткові дроби Записати числа a10 і b10 у вигляді а10·10 -3 і b10·10 -3. а10 " а10·10 -3 = 0,265 b10 " b10·10 -3 = 0,527 Перевести їх в двійкову систему числення з точністю 11 двійкових знаків по загальному правилу переводу. а) a10" a2;
a2=0,01000011110;
а) b10" b2;
b2=0,10000110111;
Перевести їх в двійкову систему числення з точністю 11 двійкових знаків через вісімкову систему числення. а10" а8" а2;
а8=0,20753412172; а2=0,010000111101011100001010001111010;
b10" b8" b2;
b8=0,41564570651; b2=0,100001101110100101111000110101001;
2.2.1.4 Записати дроби а10·10 -3 і b10·10 -3 в комірку машини з фіксованою точкою і кількістю розрядів n=8.
2.1.3. Представити дроби +а
-а
+ b
- b
2.1.4. Виконати операцію додавання (+a +b); (+a -b); (-a +b); (-a -b); у вказаних кодах. (+a +b); апк+ bпк= азк+ bзк= адк+ bдк 0,0100001 0,1000011 0,1100100 (+a -b); а) апк+(-bпк) 0, 0100001 1, 1000011 1, 1100100 б) азк+(-bзк) 0,0100001 1,0111100 1,1011101 в) адк+(-bдк) 0, 0100001 1,1010011 1,111010 (-a +b); а) -апк+ bпк 1,0100001 0,1000011 1,1100100 б) –азк+ bзк 1,1011110 0,1000011 10,0100001 в) -адк+ bдк 1,1000001 0, 1000011 10,0000100 (-a -b); а) -апк+(- bпк) 1,0100001 1,1000011 10,1100100 б) -азк+(- bзк) 1,1011110 1,0111100 11,001101 в) -адк+(- bдк) 1,1000001 1,1010011 11,001010 2.1.1 2.1.5. Виконати операцію множення дробів Зі зсувом вправо.
Зі зсувом вліво.
Зі старшого розряду, зі зсувом вліво.
Зі старшого розряду, зі зсувом вправо.
В ДК зі зсувом вправо.
2.1.6. Виконати операцію ділення двійкових дробів
B/A=0,0111111000010 – з встановленням залишку.
B/A=1 – без встановлення залишку. 2.1.7. Виконати контроль по модулю 3 всіх арифметичних операцій. Результати всіх арифметичних операцій: - 0,1100100; - 1,1100100; - 1,1011101; - 1,1110100; - 1,1100100; - 10,0100001; - 10,1100100; - 11,001101; - 11,0001010; - 0,00100010100011; - 1,1010100010011; - 10000010. Числовий метод: A10 = 265: 3 = 88 (+1); B10 = 527: 3 = 175 (+2); Цифровий метод: A10 265 = 2+6+5 = 13: 3 => 4 (+1); B10 527 = 5+2+7 = 14: 3 => 4 (+2); 0,11001002 = 1+1+0+0+1+0+0 = 3: 3 = 1 (0); 1,11001002 = 1+1+1+0+0+1+0+0 = 4: 3 = 1(+1); 1,10111012 = 1+1+0+1+1+1+0+1 = 6: 3 = 2 (0); 1,11101002 = 1+1+1+1+0+1+0+0 = 5: 3 = 1 (+2); 1,11001002 = 1+1+1+0+0+1+0+0 = 4: 3 = 1(+1); 10,01000012 = 1+0+0+1+0+0+0+0+1 = 3: 3 = 1 (0); 11,0011012 = 1+1+0+0+1+1+0+1 = 5: 3 = 1 (+2); 0,001000101000112 = 0+0+0+1+0+0+0+1+0+1+0+0+0+1+1 = 5: 3 = 1 (+2); 1,10101000100112 = 1+1+0+1+0+1+0+0+0+1+0+0+1+1 = 7: 3 = 2 (+1); 2.1.8. Результати всіх арифметичних операцій перевести в десяткову систему числення по загальному правилу переводу, через вісімкову систему числення, а також за допомогою запису числа у вигляді степеневого ряду. 0,11001002 = 1∙2-1+1∙2-2+1∙2-5 = 0,5+0,25+0,03125 = 0,7812510; 0,10111012 = 1∙2-1+1∙2-3+1∙2-4+1∙2-5+1∙2-7 = 0,5+0,125+0,0625+0,03125+0,0078125 = 0,726562510; 0,11101002 = 1∙2-1+1∙2-2+1∙2-3+1∙2-5 = 0,5+0,25+0,125+0,03125 = 0,3062510; 0,11001002 = 1∙2-1+1∙2-2+1∙2-5 = 0,5+0,25+0,03125 = 0,7812510; 10,01000012 = 1∙21+1∙2-2+1∙2-7 = 2+0,25+0,0078125 = 2,257812510; 10,11001002 = 1∙21+1∙2-1+1∙2-2+1∙2-5 = 2+0,5+0,25+0,03125 = 2,7812510; 11,0011012 = 1∙21+1∙20+1∙2-3+1∙2-4+1∙2-6 = 2+1+0,125+0,0625+0,015625 = 3,20312510; 0,001000101000112 = 1∙2-3+1∙2-7+1∙2-9+1∙2-13+1∙2-14 = 0,125+0,0078125+0,0001220703125+6,103515625E-5 = 0,1349487304687510; 0,10101000100112 = 1∙2-1+1∙2-3+1∙2-5+1∙2-9+1∙2-12+1∙2-13 = 0,5+0,125+0,03125+0,001953125+0,000244140625+0,000122073125 = 0,658969335937510; 100000102 = 1∙27+1∙21 = 128+2 = 13010;
Тепер переводимо числа з 10 системи числення у 8:
0,7812510 = 0,628;
0,726562510 = 0,563777674718
0, 3062510 = 0,234631463148;
2,257812510 = 2,2048;
2,7812510 = 2,628;
3,20312510 = 3,158;
0,1349487304687510 = 0,10573663768;
2.1.9. Виконати всі арифметичні операції в десятковій системі числення. Пояснити розбіжність результатів. Розбіжність результатів є досить незначною, та полягає у тому, що під час переведення з однієї системи числення в іншу, ми переводимо числа з певною точністю, що в свою чергу спричинює похибку.
2.2. Вихідні дані представлені у вигляді двох десяткових чисел А(10) і В(10) А = 265; B=527 2.2.1 Записати підряд двійкові числа А(2) і В(2). Перші 16 цифр отриманого запису прийняти за значення булевої функції чотирьох змінних і представити її в табличному вигляді А2 = 100001001; В2 = 100001111; Перші 16 цифр отриманого запису – 1000010011000011;
2.2.1. Виписати всі функції, які покривають задану. 1. ( 2. ( 3. ( 4. ( 5. ( 6. ( 7. 8. 9. 10. 11. ( 2.2.2. Записати в аналітичному виді ДДНФ заданої функції і мінімізувати її методом Квайна (безпосередньо по імплікантній матриці і з допомогою метода Петрика для пошуку тупикових ДНФ), методом Квайна – Мак-Класкі, а також за допомогою діаграм Вейча (карт Карно). ДДНФ: F(x1 x2 x3 x4) = ( Метод Квайна Операція склеювання: 1-2 1-3 1-4 1-5 1-6 1-7 1-8 1-9 1-10 2-3 2-4 2-5 2-6 2-7 2-8 2-9 2-10 – 2-11 3-4 3-5 3-6 3-7 3-8 3-9 3-10 3-11 4-5 4-6 4-7 4-8 4-9 4-10 4-11 5-6 5-7 5-8 5-9 – 5-10 5-11 6-7 6-8 – 6-9 6-10 6-11 7- 8 7- 9 7-10 7-11 8-9 8-10 8-11 9-10 9-11 10-11
Операція поглинання(використовуємо імпліканти тільки 3 – го рангу): F(x1 x2 x3 x4) =
Таблиця покриттів Табл. 2.1.
Fмднф= Метод Квайна-Мак-Класкі F(x1x2x3x4)=0000V0010V0011V0100V0101V0110V1000V1001V1010V1101V1110V1111. K0 = K1 =
K3 = Таблиця покриттів Табл. 2.1.
Fмднф= Карти Карно
Fмднф= | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

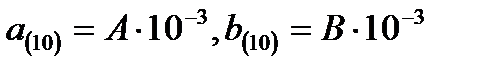 і перевести їх в двійкову систему числення з точністю 11 двійкових знаків по загальному правилу переводу, а також через вісімкову систему числення. Записати дроби
і перевести їх в двійкову систему числення з точністю 11 двійкових знаків по загальному правилу переводу, а також через вісімкову систему числення. Записати дроби  в комірку машини з фіксованою точкою і кількістю розрядів n=10. Оцінити діапазон і точність представлення чисел при прийнятій розрядності.
в комірку машини з фіксованою точкою і кількістю розрядів n=10. Оцінити діапазон і точність представлення чисел при прийнятій розрядності.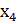


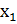
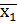


 );
);



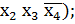

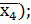

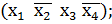
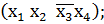

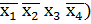 V(
V( (
( )V(
)V( (
( V
V  V(
V(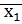

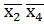

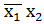



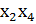

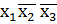

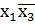




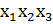
 V
V  V
V 

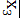
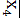 )
)

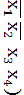
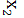
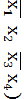

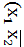
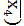
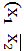
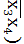

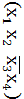

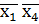





 V
V 

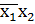

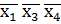 V
V 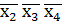 V
V  V
V  V
V  V
V  V
V 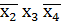 V
V  V
V  V
V  V
V  V
V 


