
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ I. Теоретичні відомостіСодержание книги Поиск на нашем сайте
ЗМІСТ ВСТУП РОЗДІЛ I. ТЕОРЕТИЧНІ ВІДОМОСТІ 1.1 Формати подання даних 1.2 Представлення числової інформації в цифровому автоматі 1.3 Арифметичні дії з двійковими числами: 1.3.1 Алгебраїчне додавання 1.3.2 Операція машинного множення 1.3.3 Операції машинного ділення 1.4 Контроль за модулем 1.5 Мінімізація функцій перемикання: 1.5.1 Методом Квайна 1.5.2 Методом Петрика 1.5.3 Методом Квайна-Мак-Класкі 1.5.4 За допомогою діаграм Вейнча (карт Карно) РОЗДІЛ II. РОЗРАХУНКОВІ ДАНІ 2.1 Вихідні дані для курсової роботи представлені у вигляді двох десяткових чисел А(10) і В(10). 2.1.1 Перевести числа А(10) і В(10) в двійкову систему числення по загальному правилу переводу, а також через вісімкову систему числення. 2.1.2 Записати десяткові дроби 2.1.3 Представити дроби 2.1.4 Виконати операцію додавання (+a +b); (+a -b); (-a +b); (-a -b); у вказаних кодах. 2.1.5 Виконати операцію множення дробів 2.1.6 Виконати операцію ділення двійкових дробів 2.1.7 Виконати контроль по модулю 3 всіх арифметичних операцій. 2.1.8 Результати всіх арифметичних операцій перевести в десяткову систему числення по загальному правилу переводу, через вісімкову систему числення, а також за допомогою запису числа у вигляді степеневого ряду. 2.1.9 Виконати всі арифметичні операції в десятковій системі числення. Пояснити розбіжність результатів. 2.2 Вихідні дані представлені у вигляді двох десяткових чисел А(10) і В(10). 2.2.1 Записати підряд двійкові числа А(2) і В(2). Перші 16 цифр отриманого запису прийняти за значення булевої функції чотирьох змінних і представити її в табличному вигляді. 2.2.2 Виписати всі функції, які покривають задану. 2.2.3 Записати в аналітичному виді ДДНФ заданої функції і мінімізувати її методом Квайна (безпосередньо по імплікантній матриці, та з допомогою метода Петрика, для пошуку тупикових ДНФ), методом Квайна – Мак-Класкі, а також за допомогою діаграм Вейнча (карт Карно).
ВИСНОВКИ СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ВСТУП Цифрові автомати (ЦА) - це пристрої що містять систему обробки дискретної інформації, ця інформація має вхід і вихід, вона служить для подачі (зняття) вхідних (вихідних) сигналів, представлених в паралельній чи послідовній формі. Будь-який цифровий автомат може бути побудований і функціонувати, якщо є алгоритм. Цифрові автомати поділяють за такими ознаками: 1) Згідно із законом функціонування цифрового автомата, автомат підрозділяється на 2 класи - 1рода і 2 роду (Милі і Мура) відмітною особливістю яких є залежність від вхідних сигналів. 2) За кінцівками множин вхідних і вихідних сигналів, а так само за множинами станів. Вони поділяються на кінцеві автомати і нескінченні автомати. 3) За обсягом пам'яті (з пам'яттю – послідовні, а без пам'яті - логічні Схеми). 4) За ступенем розкриття структури ЦА бувають абстрактні та структурні. 5) По відношенню між автоматами: підавтомат і надавтомат. 6) За повнотою використовуваних переходів з одного стану в інший (повністю і частково повні). 7) За стабільністю проходження вихідних сигналів: синхронні та асинхронні. Одноблокові та багатоблокові автомати Одноблокові автомати – це такі цифрові автомати, будь-який цифровий автомат яких складається з об'єкта управління цифрового автомата, та його взаємних сигналів між ними. Багатоблокові автомати - це такі цифрові автомати, для яких керуючий автомат реалізує функції з управління всіма блоками, тобто блок не є єдиним. Автомат Мура відрізняється від автомата Мілі законом функціонування цифрових автоматів. Вихідний сигнал автомата Мура залежить від стану в який перейде автомат, і безпосередньо не залежить від вхідного сигналу. Автомат Мура, як і будь-який інший цифровий автомат, задається своїми таблицями входу і виходу. Вихідний сигнал і стан, в який перейде автомат Мілі залежить від попереднього стану і вхідного сигналу. Так само як і в автомата Мура, автомат Мілі - як і будь-який інший цифровий автомат, задається своїми таблицями входу і виходу.
Логіка в інформатиці — це дослідження галузі знань, де логіку застосовують для роботи з штучним інтелектом, та всією інформатикою загалом. Використання логіки дуже ефективне в усіх цих областях. Формати подання даних Формати даних — це сукупність регламентованих в архітектурі ЕОМ структур, для представлення різних за специфікою обробки видів інформації (цілих чисел, дробових чисел, текстових рядків тощо). В ЕОМ інформація різного характеру представляється двійковими послідовностями з різним числом розрядів. Окремі частини цих послідовностей мають певне призначення, причому для фон-ноймановских машин ці призначення набувають сенсу тільки в контексті виконуваних команд. Поза цим контекстом і дані, і команди — усього лише послідовності двійкових розрядів, зовсім нерозрізнених за формою подання. Однак в якості операндів при виконанні команди, різні розряди цих послідовностей наділяються певним змістом. Тому говорять, що у фон-ноймановских машинах типи даних визначаються не самими даними, а операцією, що над ними виконується. Та якщо, в регістри-джерела операндів команди арифметичного додавання раптом виявилися завантажені розряди слова, яке містить якийсь текст, а не числа, то фон-нойманівська ЕОМ просто проігнорує ту обставину, що навряд чи має сенс додавати два текстові рядки, і поведеться з ними як з числами. Але це зовсім не зменшує важливості форматів даних у фон-нейманівских машинах, адже специфіка виконання тих чи інших машинних команд визначається тим форматом даних, над яким вони діють (інша справа, що фактичні операнди можуть не відповідати цьому форматові, але це вже лежить на відповідальності програміста. Вся ця безліч операцій, а за ними й формати даних, можна розбити на дві великих групи: цілочисельні формати й формати для чисел із плаваючою комою. Числа з фіксованою комою. У разі використання чисел із фіксованою комою, представлення коми не виконується, але вважається що вона є на певній, наперед відомій позиції відносно розрядів числа. Найчастіше вважається, що кома стоїть біля молодшого розряду (таким чином представляються дробові числа), хоча можливе і застосування змішаного варіанту. У такому форматі представляються числа з діапазону –1 < число < 1 (якщо є знаковий розряд) або 0 < число < 1 (якщо знакового розряду немає). Числа із рухомою комою. Для однозначного і максимально точного відображення чисел з рухомою комою їх представляють в нормалізованому вигляді. Якщо виконується нерівність q-1< = m < 1 а у випадку війкової системи числення 0,5 < = м < 1 (старший двійковий розряд мантиси дорівнює 1), то вважається, що число представлене в нормалізованому вигляді. Таким чином у двійкового, нормалізованого числа в форматі з рухомою комою мантиса є правильним дробом, а у старшому розряді мантиси завжди стоїть 1. Нормалізація чисел у комп’ютері виконується або апаратно, або за допомогою спеціальної програми. Для цієї мети виділяють: 1) По одному розряду, для представлення знаку числа Sm і знаку порядку Sp. 2) Певне число розрядів, для представлення значення порядку р. 3) Розряди для представлення модуля мантиси. Алгебраїчне додавання Додавання здійснюється послідовно, починаючи з молодшого розряду. У кожному розряді додаються значення трьох величин: розряду операнда аі, розряду операнда bі, та переносу з попереднього розряду pi-1. У результаті додавання в кожному розряді одержуємо дві величини: значення суми sі, та значення переносу в наступний, більш старший розряд.
Операція машинного множення Множення двійкових чисел виконують у прямому коді. Знак добутку визначають за знаковими розрядами множеного і множника у відповідності з таким правилом: якщо знак операндів однаковий, то знак добутку - позитивний; у противному випадку знак добутку негативний. Знак добутку двох чисел не впливає на алгоритм виконання операції множення модулів цих чисел. Найпростішим способом множення є багаторазове додавання, що полягає в додаванні множеного самого із собою, причому число таких операцій дорівнює множнику. Такий алгоритм множення є простим, але повільним. Часто використовують спосіб множення, процедура якого аналогічна процедурам множення вручну. У цьому випадку результат одержують додаванням часткових добутків, що є результатом множення множеного на значення чергових розрядів множника. Кожен частковий добуток удвічі перевищує попереднє значення, що відповідає зрушенню його ліворуч на один розряд. Операції машинного ділення В універсальних обчислювальних машинах, як правило, реалізується "шкільний" алгоритм ділення чисел. "Шкільний" алгоритм ділення полягає в тому, що дільник на кожному кроці віднімається від діленого стільки разів (починаючи зі старших розрядів), скільки це можливо для отримання найменшого позитивного залишку. Тоді в черговий розряд частки записується цифра, що дорівнює числу дільників, що містяться в діленому на даному кроці. При діленні операцію віднімання повторюють до тих пір, поки ділене не стане менше дільника. Існують і інші алгоритми, наприклад, алгоритм ділення з відновленням залишку, та алгоритм ділення без відновлення залишку. Контроль за модулем Контроль за модулем визнаний одним з основних методів функціонального діагностування обчислювальних пристроїв (ОП). Однак реалізація контролю за модулем для сучасних ВУ є складним завданням, що пов'язано з високими вимогами, які пред'являються до продуктивності ВУ, діапазону представлення чисел і точності обчислень. Такому рівню вимог відповідають матриці обчислювального пристрою з плаваючою точкою, в яких мантиси чисел обробляються зі збереженням єдиних форматів представлення операндів і результатів. Витрати обладнання і часу обчислень в матричних обчислювальних пристроях знаходяться відповідно в квадратичної і лінійної залежності від розрядності оброблюваних чисел. Для зниження цих витрат доцільно використовувати методи скороченого виконання операцій. Однак скорочення обчислень суперечить використанню традиційного контролю за модулем, вимагаючи його розвитку. Завдання контролю за модулем скороченою операції вирішена для матричного помножувача, що забезпечує для ВУ одночасно і високу достовірність функціонування і високі схемо-технічні показники, близькі до двократного зниження витрат обладнання і підвищення швидкодії. Розподіл чисел є найскладнішою арифметичною операцією і вимагає для її реалізації найбільших витрат обладнання і часу. Пропонується скорочене виконання операції ділення - її контроль за модулем.
Найбільш часто в матричних ВУ використовуються алгоритми ділення з відновленням і без відновлення залишку. Існує два методи отримання контрольного коду: числовий і цифровий. Метод Квайна Цей метод базується на перетвореннях досконалої диз’юнктивної нормальної форми за допомогою операції неповного склеювання та поглинання. Операція (повного) склеювання визначається співвідношенням: Справедливість даного виразу випливає з такого перетворення: Операція поглинання визначається співвідношенням: Кажуть, що член xy поглинається є членом x. Справедливість сказаного випливає з перетворень: Операція неповного склеювання, що застосована в методі Квайна, визначається формулою Теорема Квайна Якщо в досконалій диз’юнктивній нормальній формі логічної функції провести всі операції неповного склеювання, а потім всі операції поглинання, то вийде скорочена диз’юнктивна нормальна форма цієї функції, тобто диз’юнкція всіх її простих імплікант. З теореми Квайна випливає – якщо функція задана у довільній формі, то її слід перетворити в досконалу ДНФ, застосувати функцію розгортання, і лише після цього проводити операції склеювання і поглинання. Метод Петрика Метод використовується для знаходження всіх мінімальних покриттів конституант одиниці і дозволяє отримати всі тупикові ДНФ по імплікантній матриці. Суть методу полягає в наступному. За імплікантною матрицею будується, так зване кон'юнктивне уявлення імплікантной матриці. Для цього всі прості імпліканти позначаються різними літерами (зазвичай великими латинськими). Після цього, для кожного стовпчика імплікантної матриці будується диз'юнкція всіх букв, що позначають рядки матриці, перетин яких з стовпцем відзначено хрестиком. Кон'юнктивні уявлення імплікантної матриці утворюється як кон'юнкція побудованих диз'юнкцій для всіх стовпців матриці. До кон'юнктивного подання матриці можуть бути застосовані всі співвідношення булевої алгебри, з метою його спрощення. Після розкриття дужок і виконання всіх можливих поглинань виходить диз'юнкція і кон'юнкція, кожна з яких містить всі імпліканти тупикової ДНФ. Метод Квайна-Мак-Класкі Метод Квайна-Мак-Класкі (метод простих імплікант) – табличний метод мінімізації булевих функцій, розроблений Вілардом Квайном і Едвардом Мак-Класкі. Функціонально він ідентичний картам Карно, але таблична форма робить його ефективнішим для використання в комп'ютерних алгоритмах.
Алгоритм мінімізації Терми (кон'юнктивні - в разі СДНФ і диз'юнктивні - в разі СКНФ), на яких визначена ФАЛ записуються у вигляді їх довічних еквівалентів. Ці еквіваленти розбиваються на групи, в кожну групу входять еквіваленти з рівною кількістю одиниць (нулів). Проводиться попарне порівняння еквівалентів (термів) в сусідніх групах, з метою формування термів нижчих рангів. Складається таблиця з заголовком рядків, в якій є вихідні терми, а в заголовках стовпців є терми низьких рангів. Розставляються мітки, що відображають поглинання термів вищих рангів (вихідних термів) і далі мінімізація проводиться за методом Квайна. Метод Квайна-Мак-Класкі F(x1x2x3x4)=0000V0010V0011V0100V0101V0110V1000V1001V1010V1101V1110V1111. K0 = K1 =
K3 = Таблиця покриттів Табл. 2.1.
Fмднф= Карти Карно
Fмднф= ВИСНОВКИ Мною були узагальнені знання з мінімізації функції різними методами: Квайна, Квайна-Мак-Класкі, Петрика та Карт Карно. Розглянуті алгоритми кожного методу. Розширено знання з прикладної теорії цифрових автоматів. В завданні розглянув питання представлення чисел, алгоритми виконання основних арифметичних операцій та їх контролю. Вдосконалено знання з контролю по модулю, з форматів подання даних, з переводу з однієї системи числення в іншу. Розглянуто арифметичні дії над двійковими числами, представлення чисел в цифровому форматі. Виконав операції додавання у вказаних кодах, виконав операції множення, операції ділення чисел, взяття отриманого числа за значення булевої функції чотирьох змінних і представив її в табличному вигляді запис в аналітичному вигляді ДДНФ заданої функції. СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 1. Зельдович Б. Мышкис А.Д «Элементы прикладной математики». 2. Т.С. Соболева «Дискретна інформатика та математика». 3. В.І. Жабін І.А. Жуков І.А. Клименко В.В. Ткаченко «Прикладна теорія цифрових автоматів». 4. Матвієнко М.П. «Комп’терна логіка». 5. Апраксін Ю.К. «Основы теории и проектирования цифровых автоматов: Учеб. пособ. для вузов». 6. Понаморев В.С., Красников В.В. Методические указания по курсу «Организация и функционирование ЭВМ и систем». Ч.1. Арифметические основы ЭВМ. ДГТУ, 1996. 7. Бровков В.Г., Богатова О.О. «Прикладная теория цифровых автоматов». 8. Савельев А.Я. «Прикладная теория цифровых автоматов» 9. Куліковський Л.Ф. Мотов В.В. «Теоретичні основи інформаційних процесів». 10. В.С. Князьков Т.В.Волченський «Введение в теорію автоматов». 11. Самофалов К.Г., Риманкевич А.М. и др. «Прикладная теория цифровых автоматов». 12. Ю.Г.Карпов «Теория Автоматов». 13. В.Б. Кудрявцев С.В.Алешин «Введение в теорію атвоматов». 14. Джон Фон Нейман «Теория самовоспроизводящихся автоматов». 15. И.В. Потапов «Єлементі прикладной теории цировіх автоматов». 16. Гашков С.Б. Системи исчисления и их переменные. МЦИМО, 2004-53с.
ЗМІСТ ВСТУП РОЗДІЛ I. ТЕОРЕТИЧНІ ВІДОМОСТІ 1.1 Формати подання даних 1.2 Представлення числової інформації в цифровому автоматі 1.3 Арифметичні дії з двійковими числами: 1.3.1 Алгебраїчне додавання 1.3.2 Операція машинного множення 1.3.3 Операції машинного ділення 1.4 Контроль за модулем 1.5 Мінімізація функцій перемикання: 1.5.1 Методом Квайна 1.5.2 Методом Петрика 1.5.3 Методом Квайна-Мак-Класкі 1.5.4 За допомогою діаграм Вейнча (карт Карно) РОЗДІЛ II. РОЗРАХУНКОВІ ДАНІ 2.1 Вихідні дані для курсової роботи представлені у вигляді двох десяткових чисел А(10) і В(10). 2.1.1 Перевести числа А(10) і В(10) в двійкову систему числення по загальному правилу переводу, а також через вісімкову систему числення. 2.1.2 Записати десяткові дроби 2.1.3 Представити дроби 2.1.4 Виконати операцію додавання (+a +b); (+a -b); (-a +b); (-a -b); у вказаних кодах. 2.1.5 Виконати операцію множення дробів 2.1.6 Виконати операцію ділення двійкових дробів 2.1.7 Виконати контроль по модулю 3 всіх арифметичних операцій. 2.1.8 Результати всіх арифметичних операцій перевести в десяткову систему числення по загальному правилу переводу, через вісімкову систему числення, а також за допомогою запису числа у вигляді степеневого ряду. 2.1.9 Виконати всі арифметичні операції в десятковій системі числення. Пояснити розбіжність результатів. 2.2 Вихідні дані представлені у вигляді двох десяткових чисел А(10) і В(10). 2.2.1 Записати підряд двійкові числа А(2) і В(2). Перші 16 цифр отриманого запису прийняти за значення булевої функції чотирьох змінних і представити її в табличному вигляді. 2.2.2 Виписати всі функції, які покривають задану. 2.2.3 Записати в аналітичному виді ДДНФ заданої функції і мінімізувати її методом Квайна (безпосередньо по імплікантній матриці, та з допомогою метода Петрика, для пошуку тупикових ДНФ), методом Квайна – Мак-Класкі, а також за допомогою діаграм Вейнча (карт Карно). ВИСНОВКИ СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ВСТУП Цифрові автомати (ЦА) - це пристрої що містять систему обробки дискретної інформації, ця інформація має вхід і вихід, вона служить для подачі (зняття) вхідних (вихідних) сигналів, представлених в паралельній чи послідовній формі. Будь-який цифровий автомат може бути побудований і функціонувати, якщо є алгоритм. Цифрові автомати поділяють за такими ознаками: 1) Згідно із законом функціонування цифрового автомата, автомат підрозділяється на 2 класи - 1рода і 2 роду (Милі і Мура) відмітною особливістю яких є залежність від вхідних сигналів. 2) За кінцівками множин вхідних і вихідних сигналів, а так само за множинами станів. Вони поділяються на кінцеві автомати і нескінченні автомати. 3) За обсягом пам'яті (з пам'яттю – послідовні, а без пам'яті - логічні Схеми). 4) За ступенем розкриття структури ЦА бувають абстрактні та структурні. 5) По відношенню між автоматами: підавтомат і надавтомат. 6) За повнотою використовуваних переходів з одного стану в інший (повністю і частково повні). 7) За стабільністю проходження вихідних сигналів: синхронні та асинхронні. Одноблокові та багатоблокові автомати Одноблокові автомати – це такі цифрові автомати, будь-який цифровий автомат яких складається з об'єкта управління цифрового автомата, та його взаємних сигналів між ними. Багатоблокові автомати - це такі цифрові автомати, для яких керуючий автомат реалізує функції з управління всіма блоками, тобто блок не є єдиним. Автомат Мура відрізняється від автомата Мілі законом функціонування цифрових автоматів. Вихідний сигнал автомата Мура залежить від стану в який перейде автомат, і безпосередньо не залежить від вхідного сигналу. Автомат Мура, як і будь-який інший цифровий автомат, задається своїми таблицями входу і виходу. Вихідний сигнал і стан, в який перейде автомат Мілі залежить від попереднього стану і вхідного сигналу. Так само як і в автомата Мура, автомат Мілі - як і будь-який інший цифровий автомат, задається своїми таблицями входу і виходу. Логіка в інформатиці — це дослідження галузі знань, де логіку застосовують для роботи з штучним інтелектом, та всією інформатикою загалом. Використання логіки дуже ефективне в усіх цих областях. РОЗДІЛ I. ТЕОРЕТИЧНІ ВІДОМОСТІ Формати подання даних Формати даних — це сукупність регламентованих в архітектурі ЕОМ структур, для представлення різних за специфікою обробки видів інформації (цілих чисел, дробових чисел, текстових рядків тощо). В ЕОМ інформація різного характеру представляється двійковими послідовностями з різним числом розрядів. Окремі частини цих послідовностей мають певне призначення, причому для фон-ноймановских машин ці призначення набувають сенсу тільки в контексті виконуваних команд. Поза цим контекстом і дані, і команди — усього лише послідовності двійкових розрядів, зовсім нерозрізнених за формою подання. Однак в якості операндів при виконанні команди, різні розряди цих послідовностей наділяються певним змістом. Тому говорять, що у фон-ноймановских машинах типи даних визначаються не самими даними, а операцією, що над ними виконується. Та якщо, в регістри-джерела операндів команди арифметичного додавання раптом виявилися завантажені розряди слова, яке містить якийсь текст, а не числа, то фон-нойманівська ЕОМ просто проігнорує ту обставину, що навряд чи має сенс додавати два текстові рядки, і поведеться з ними як з числами. Але це зовсім не зменшує важливості форматів даних у фон-нейманівских машинах, адже специфіка виконання тих чи інших машинних команд визначається тим форматом даних, над яким вони діють (інша справа, що фактичні операнди можуть не відповідати цьому форматові, але це вже лежить на відповідальності програміста. Вся ця безліч операцій, а за ними й формати даних, можна розбити на дві великих групи: цілочисельні формати й формати для чисел із плаваючою комою. Числа з фіксованою комою. У разі використання чисел із фіксованою комою, представлення коми не виконується, але вважається що вона є на певній, наперед відомій позиції відносно розрядів числа. Найчастіше вважається, що кома стоїть біля молодшого розряду (таким чином представляються дробові числа), хоча можливе і застосування змішаного варіанту. У такому форматі представляються числа з діапазону –1 < число < 1 (якщо є знаковий розряд) або 0 < число < 1 (якщо знакового розряду немає). Числа із рухомою комою. Для однозначного і максимально точного відображення чисел з рухомою комою їх представляють в нормалізованому вигляді. Якщо виконується нерівність q-1< = m < 1 а у випадку війкової системи числення 0,5 < = м < 1 (старший двійковий розряд мантиси дорівнює 1), то вважається, що число представлене в нормалізованому вигляді. Таким чином у двійкового, нормалізованого числа в форматі з рухомою комою мантиса є правильним дробом, а у старшому розряді мантиси завжди стоїть 1. Нормалізація чисел у комп’ютері виконується або апаратно, або за допомогою спеціальної програми. Для цієї мети виділяють: 1) По одному розряду, для представлення знаку числа Sm і знаку порядку Sp. 2) Певне число розрядів, для представлення значення порядку р. 3) Розряди для представлення модуля мантиси.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.202.169 (0.013 с.) |

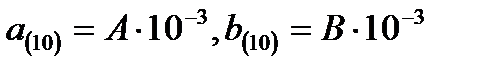 і перевести їх в двійкову систему числення з точністю 11 двійкових знаків по загальному правилу переводу, а також через вісімкову систему числення. Записати дроби
і перевести їх в двійкову систему числення з точністю 11 двійкових знаків по загальному правилу переводу, а також через вісімкову систему числення. Записати дроби  в комірку машини з фіксованою точкою і кількістю розрядів n=10. Оцінити діапазон і точність представлення чисел при прийнятій розрядності.
в комірку машини з фіксованою точкою і кількістю розрядів n=10. Оцінити діапазон і точність представлення чисел при прийнятій розрядності. .
. .
. .
. /
/ , яка може бути отримана з формул: x=x
, яка може бути отримана з формул: x=x  =x
=x 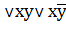 .
.


 V
V  .
.




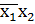


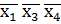 V
V 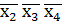 V
V  V
V  V
V  V
V  V
V 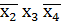 V
V  V
V  V
V  V
V  V
V 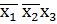 .
.


