
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез кодовой комбинации циклического кодаСодержание книги
Поиск на нашем сайте Вывод ЦК является разновидностью систематических кодов и обладает всеми их свойствами. Он имеет высокие корректирующие свойства, широко применяется на практике, особенно в современных телекоммуникационных технологиях. Ознакомился с параметрами ЦК, способами получения кодовой комбинации. Практическим путем синтезировал кодовую комбинацию ЦК и с помощью образующего полинома проверил ее правильность.
КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ СВЕРТОЧНЫХ КОДОВ Построение схемы кодера и решетчатой диаграммы Кодер двоичного сверточного кода (СК) содержит регистр сдвигов на К разрядов и сумматоры по модулю 2 для образования кодовых символов. Входы сумматоров определены разрядами регистра. Связи ш-го сумматора с ячейками о-го регистра описывают порождающим многочленом Исходные данные
1. Рассмотрим простейший несистематический код (7,5): Для получения образующего полинома переведем цифры в двоичную и полиномиальную форму
рис. 2.1 – Функциональная схема кодера НСК (7,5) Функции переходов со значениями входных и выходных сигналов могут быть представлены с помощью графов состояний, что принято называть диаграммой состояний. ДС кодера СК отвечает всем требованиям и является автоматом Мили. На рис. 2 в прямоугольных рамках указаны состояния кодера
рис. 2.2 – Диаграмма состояний кодера (7,5)
 – невозможно. – невозможно.
рис. 2.3 – Решетчатая диаграмма кодера (7,5)
2.
Выбираем таблицу 7х7для
Избыточность определяется:
3.
Общая последовательность состоит из параллельных
Ошибки в 3 и 9 символах
3 ПОСТРОЕНИЕ КАДРОВ ПО ПРОЦЕДУРЕ НД1_С Формирование I-кадра
рис. 3.1 – Структура кадра Кадр состоит из 6 полей. Рассмотрим построение полей кадров: 1. Поля начала и конца кадров. Для определения начала и конца кадра используется принцип стартстопной цикловой синхронизации. Применяется комбинация вида 01111110. 2. Поле адреса. В этом поле передается адрес (номер) соответствующей станции, представленный в двоичной форме. Каждой станции присваивается уникальный адрес. В кадре, содержащем команды, передается адрес удаленной станции, а в кадре-ответе передается местный (свой) адрес. Допускается расширение поля адреса еще на 8 бит. Указателем на то, что следующий байт кадра входит в область адреса, является наличие 0 в первом (младшем) бите предыдущего байта поля адреса, исключая байт вида 00000000. Таким образом, младший разряд обычного (не расширенного) адреса должен быть равен 1. 3. Поле управления. Содержит идентификаторы типа кадра и операций протокола HDLC. Основной (8-битовый) формат поля управления:
рис. 3.2 - Основной формат поля управления Ns – биты порядкового номера данного (передаваемого) I-кадра (по модулю 8). Номер группы. Nr- биты порядкового номера ожидаемого кадра (по модулю 8), то есть подтверждается правильный прием I-кадров до номера Nr-1 включительно. Номер ожидаемого кадра равен 0. P/F – бит опроса/окончания опроса. В кадре команды этот бит интерпретируется как бит опроса P (poll). Если на посылаемый кадр необходимо получить ответ (квитанцию), то выставляется P=1; если ответ не нужен, P=0. В кадре ответа этот бит интерпретируется как бит окончания опроса – F (finish). Брать любое значение. 4. Поле проверки. Контрольная последовательность, полученная в результате кодирования циклическим кодом с образующим полиномом Вставка битов – при передаче в канал связи кадра его содержимое между двумя флагами (начала и конца) не должно иметь фрагментов вида 01111110, иначе это будет идентифицироваться приемником как конец кадра. С целью создания прозрачного канала, содержимое сформированного кадра перед отправкой в канал подвергается специальной отработке. Если в последовательности встречается пять единиц подряд, то после них вставляется 0. На приеме, перед дешифрованием кадра производится обратная операция, если после пяти подряд следующих единиц есть 0, то он исключается. Этот метод называется вставкой битов (bitstuffing).
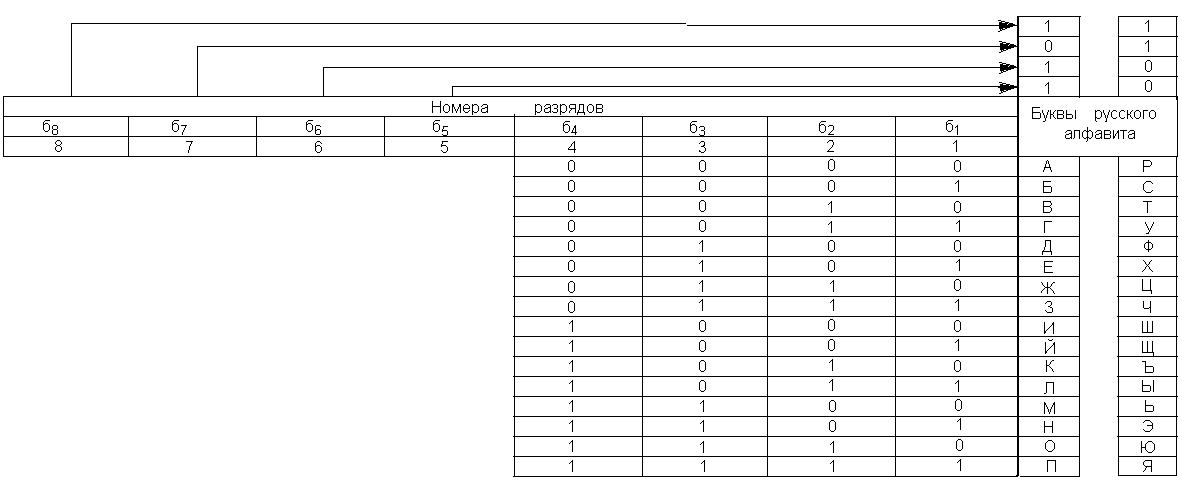
СИНТЕЗ КОДОВОЙ КОМБИНАЦИИ ЦИКЛИЧЕСКОГО КОДА 1.1 Составление информационного блока Необходимо составить информационный блок, состоящий из трех прописных букв – инициалов фамилии, имении отчества студента. Для составления необходимо использовать фрагмент кодовой таблицы первичного кода КОИ-8, который представлен на рис.1. Старшие биты считываются из первых четырех строк, а младшие – из первых четырех столбцов, соответствующих месторасположению буквы на рисунке.
Рисунок 1.1 – Код КОИ-8. Фрагмент русского алфавита Закодируем инициалы Колесник Сергей Владимирович: Ч→1011 1010 К→1011 1000 А→1100 0001
1.2 Выбор образующего полинома циклического кода Очевидно, что введение необходимой величины избыточности будет определяться длиной информационной части k, заданным значением допустимой вероятности ошибки Для инженерных расчетов широкое применение нашла модель потока ошибок, предложенная Л.П.Пуртовым, которая с достаточной для практики точностью описывает характеристики потока ошибок с пакетированием. Исследую статистику ошибок в канале связи, было замечено, что вероятность появления ошибок кратности t в n разрядной кодовой комбинации равна:
где Для канала без группирования (без памяти) Для обнаружения числа ошибок кратностью t необходим циклический код с кодовым расстоянием
С некоторым приближением можно связать вероятность появления ошибок кратности t [ P(
При расчете на ПКудобнее пользоваться десятичными логарифмами. После преобразований:
Так как в этой формуле n = k + r, требуемое значение r может быть определено путем подбора величины r, удовлетворяющее неравенству:
Зная величину r, т.е. величину высшей степени образующего полинома, следует выбрать соответствующий полином из таблицы 4. Рассчитаем количество проверочных символов и выберем образующий полином для следующих исходных данных: · Вероятность ошибки в канале связи · Вероятность необнаруженной ошибки декодером · Минимальное кодовое расстояние · Коэффициент группирования Подставим в формулу (6) исходные данные, а также значение r, начиная с 3: r = 6 6 r = 1010 неравенство не выполняется r = 14 14
неравенство выполняется. Поэтому, значение r = 14. Для выбора образующего полинома из таблицы 4 справочного материала для выполнения курсовой работы можно воспользоваться любым из трех приведенных полиномов для количества проверочных символов, равного14. Выберем полином:
1.3 Синтез кодовой комбинации циклического кода Кодовая комбинация циклического кода может быть получена двумя способами. Первый получается умножением информационной последовательности на образующий полином P(x), что приводит к формированию неразделимого циклического кода. Неразделимость значительно усложняет процесс декодирования, поэтому на практике чаще используют второй способ, при котором информационная последовательность умножается на одночлен F(x) = где F(x) – кодовая комбинация циклического кода; G(x) – информационная последовательность в полиномиальной форме; R(x) = Для перевода двоичной последовательности в полиномиальную форму каждый бит умножается на x в степени, соответствующей месторасположению этого бита. Приведем нашу последовательность, полученную в п. 1.1 в полиномиальную форму.
Полученную кодовую комбинацию можно записать как: G(x) = Умножим G(x) на одночлен G(x)
Для получения разрешенной комбинации циклического кода разделим полученную последовательность на выбранный в п. 1.2 образующий полином. Процесс деления показан ниже.
Итак, разрешенная комбинация циклического кода, в соответствии с формулой (7) имеет вид: F(x) = Переведем ее в двоичный вид:
1.4 Проверка правильности получения разрешенной КК Проверку правильности кодовой комбинации циклического кода проведем в двоичной форме. Для этого необходимо последовательность F(x) в двоичной форме сложить по модулю 2 с образующим полиномом P(x), также взятым в двоичной форме (P(x) →10011001). В случае правильности построения, получим нуль. Проверим это ниже.
Так как остаток от деления получился равным нулю, то формирование разрешенной кодовой комбинации циклического кода было верным. Вывод ЦК является разновидностью систематических кодов и обладает всеми их свойствами. Он имеет высокие корректирующие свойства, широко применяется на практике, особенно в современных телекоммуникационных технологиях. Ознакомился с параметрами ЦК, способами получения кодовой комбинации. Практическим путем синтезировал кодовую комбинацию ЦК и с помощью образующего полинома проверил ее правильность.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 1011101010111000110000011011110011111
1011101010111000110000011011110011111

 которым соответствует содержание двух крайних правых ячеек регистра сдвига кодера.
которым соответствует содержание двух крайних правых ячеек регистра сдвига кодера. - минимальное кодовое расстояние, для сверточных кодов – свободное расстояние. Определяется как минимальный выходной вес пути по решетчатой диаграмме, начинающейся и заканчивающейся в нулевом состоянии
- минимальное кодовое расстояние, для сверточных кодов – свободное расстояние. Определяется как минимальный выходной вес пути по решетчатой диаграмме, начинающейся и заканчивающейся в нулевом состоянии  . Согласно решетчатой диаграмме минимальный вес пути
. Согласно решетчатой диаграмме минимальный вес пути  равен 5, так как ему соответствует
равен 5, так как ему соответствует  .
.



 :
:



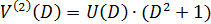

 на входе кодера:
на входе кодера: 11 10 11 00 11 01 01 11 11 10 11 11 11 11 10 10 00 01 01 11 00 11 01 10 10 01 11 00 11 01 01 00 01 01 11 00 01 01 11 11 10 11 11 01 01 11 00 00
11 10 11 00 11 01 01 11 11 10 11 11 11 11 10 10 00 01 01 11 00 11 01 10 10 01 11 00 11 01 01 00 01 01 11 00 01 01 11 11 10 11 11 01 01 11 00 00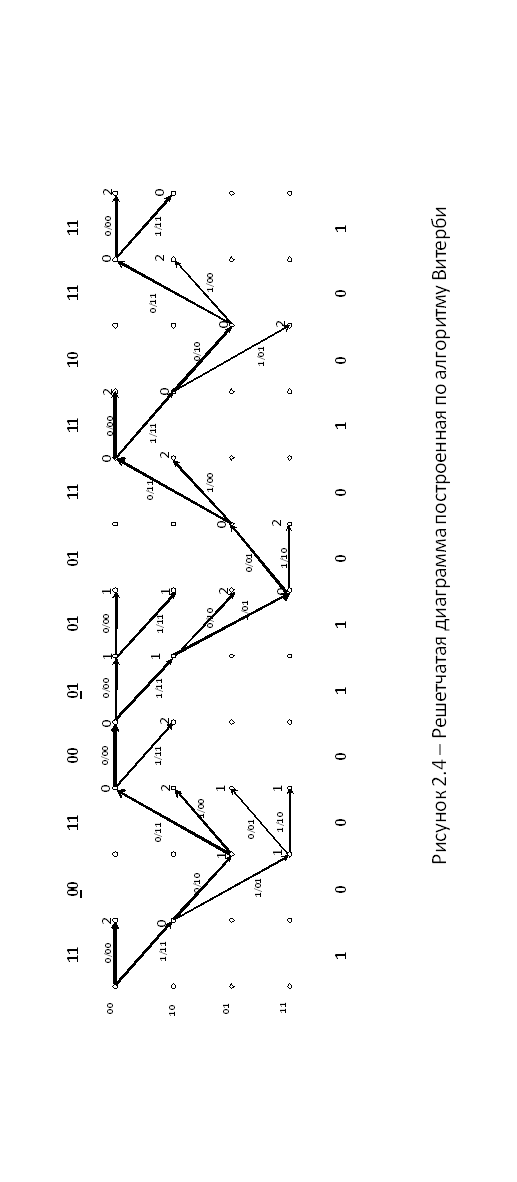
 . В качестве k информационных разрядов, которые будут защищены корректирующим кодом, берутся разряды полей: адреса, управления и информации. Таким образом, содержимое между флагами начала и конца является кодовой комбинацией ЦК. Контрольная последовательность является остатком
. В качестве k информационных разрядов, которые будут защищены корректирующим кодом, берутся разряды полей: адреса, управления и информации. Таким образом, содержимое между флагами начала и конца является кодовой комбинацией ЦК. Контрольная последовательность является остатком  .
.
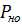 , кратностью обнаруживаемых ошибок
, кратностью обнаруживаемых ошибок  и качеством самого канала связи.
и качеством самого канала связи. ;
;
 , а при
, а при  ошибки сосредоточены в одном пакете.
ошибки сосредоточены в одном пакете.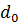 не менее
не менее  тогда формула (1) примет вид:
тогда формула (1) примет вид: .
.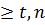 ) ] с вероятностью необнаруженной УЗО ошибки
) ] с вероятностью необнаруженной УЗО ошибки 
 и, выполнив преобразование, вычислим r
и, выполнив преобразование, вычислим r
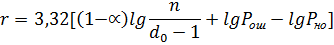
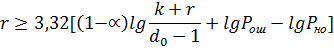




 3,32[(1-0,5)log
3,32[(1-0,5)log  – неравенство не выполняется
– неравенство не выполняется –
– –
– .
. и добавляется остаток от деления полученной последовательности на образующий полином. Это можно записать в виде формулы:
и добавляется остаток от деления полученной последовательности на образующий полином. Это можно записать в виде формулы:
 – остаток от деления на образующий полином.
– остаток от деления на образующий полином.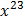 +
+ 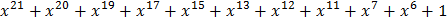
 .
.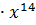 =
=  +
+ 
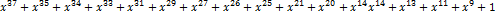
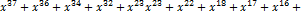
 +
+ 








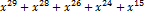

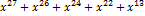

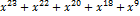


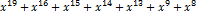


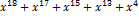






 = R(x)
= R(x)



