
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для какого случая получено решение задачи об осадке фундамента, в котором учитывается влияние всех компонентов напряжений.Содержание книги
Поиск на нашем сайте Для однородного изотропного грунта, у которого и модуль деформации Е0 и коэффициент Пуассона μ0 постоянны. 88. Как вычислить значения модуля деформации грунта Еог необходимые для расчета осадки, по результатам штамповых испытаний в поле или компрессионных испытаний в одометре? На кривой "осадка-нагрузка" штампа выбираются две точки, в пределах которых ведется спрямление. Рекомендуется, чтобы первая точка соответствовала бы давлению в грунте в точке отбора образца от собственного веса вышележащих слоев Р1, а вторая соответствовала бы полному давлению Р2 от веса грунта иожидаемой нагрузки от сооружения. Имеется в виду, что кривая в диапазоне выбранных двух давлений хорошо бы аппроксимировалась прямой. Для вычисления модуля деформации Ео, МПа, используется формула
Где е1 и е2 - значения коэф. пористости, соответствующие давлениям р1 и р2 е0 –начальный коэф. пористости.
а)штамповые испытания; б) компрессионные испытания
89. Этим способом предлагается пользоваться; еслимодуль деформации грунта основания более 100 МПа или если модуль деформации Ео > 10 МПа; но ширина подошвы фундамента более 10 м. В этом случае осадочное давление считается равным полному. 90. Потому, что полупространство снизу не ограничено (толщина равна бесконечности) и при решении задачи отыскивается несобственный интеграл. Если бы толщина была ограничена конечным размером, она входила бы в окончательную формулу осадки. 91. От каких факторов зависит коэффициент ω в формуле осадки для полупространства? Чему он равен для круга, квадрата, "ленты"? Этот коэффициент зависит от формы в плане загруженной площадки (квадрат, круг, прямоугольник), а также от жесткости штампа (гибкий штамп или жесткий). Для круга и жесткого штампа он равен 0,79, для квадрата - 0,88, для "ленты" (соотношение размеров сторон 10:1 и более) - 2,12.
С чем связано то обстоятельство, что грунты деформируются не сразу после приложения нагрузки, а на это требуется определённое время? Это связано с тем, что деформация грунта определяется изменением его пористости и для деформирования грунта нужно деформирование междучастичных связей. Эти связи часто бывают вязко-пластичными и деформируются не сразу, а с течением времени. Кроме того, в порах грунта содержится вода и изменение пористости, особенно полностью водонасыщенного грунта, связано с необходимостью отжатая воды из пор грунта, на что требуется время.
С какой скоростью в твердых телах распространяются напряжения? В твердых телах напряжения распространяются со скоростью звука.
Какой представляется модель полностью водонасыщенного глинистого грунта? Что моделирует диаметр отверстий в поршне? К. Терцаги предложил для полностью водонасыщенного глинистого грунта такую модель: цилиндр, заполненный водой, внутри которого имеется стальная пружина. Цилиндр закрыт поршнем, имеющим весьма малые отверстия. Если на этот поршень поставить груз, то опускание поршня возможно только за счет выдавливания из цилиндра лишней воды. Поршень начнет надавливать на пружину и остановится лишь тогда, когда все усилия груза полностью передадутся на пружину. При этом лишняя вода из цилиндра выдавится наружу. Диаметр отверстий моделирует фильтрационную способность грунта - чем мельче отверстия, тем медленнее выдавливается вода и медленнее идет процесс осадки.(см. рис.)
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


 Здесь S2 и S1 - см –величины осадки, соответствующие давлениям Р1 и Р2,МПа; d –диаметр штампа, см; ω- коэффициент формы штампа, равный 0,85; μ0 - коэффициент Пуассона грунта, принимаемый обычно 0,3 для песков и супесей и 0,4 для глин. По результатам компрессионных испытаний в одометре величина Е0,МПа, вычисляется по формуле:
Здесь S2 и S1 - см –величины осадки, соответствующие давлениям Р1 и Р2,МПа; d –диаметр штампа, см; ω- коэффициент формы штампа, равный 0,85; μ0 - коэффициент Пуассона грунта, принимаемый обычно 0,3 для песков и супесей и 0,4 для глин. По результатам компрессионных испытаний в одометре величина Е0,МПа, вычисляется по формуле: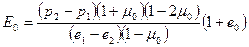



 Когда рекомендуется применять способ расчета осадки с использованием расчетной схемы в виде линейно-деформируемого слоя конечной толщины?
Когда рекомендуется применять способ расчета осадки с использованием расчетной схемы в виде линейно-деформируемого слоя конечной толщины? Почему в формулу осадки для жесткого штампа на упругом полупространстве не входит глубина сжимаемой толщи?
Почему в формулу осадки для жесткого штампа на упругом полупространстве не входит глубина сжимаемой толщи?



