
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для кого и для чего это пособие?Содержание книги
Поиск на нашем сайте
СОДЕРЖАНИЕ ПРЕДИСЛОВИЕ.. 4 1. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ.. 9 2. ЗАКОНЫ НЬЮТОНА.. 26 3. ИМПУЛЬС.. 40 4. РАБОТА. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ.. 53 5. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ В СТАЦИОНАРНЫХ ПОТЕНЦИАЛЬНЫХ ПОЛЯХ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ.. 66 6. МОМЕНТ ИМПУЛЬСА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК. УРАВНЕНИЕ МОМЕНТОВ 76 7. ДИНАМИКА ТВЕРДОГО ТЕЛА.. 91 8. ДВИЖЕНИЕ ТЕЛ В НЕИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА. СИЛЫ ИНЕРЦИИ 122 9. КОЛЕБАНИЯ.. 141 ПРЕДИСЛОВИЕ Для кого и для чего это пособие? Пособие предназначено для студентов технических специальностей, изучающих курс общей физики. В нём разобраны решения задач различной сложности по всем основным темам из раздела "Механика" курса общей физики. Пособие рассчитано на применение совместно с учебниками по курсу общей физики И.В. Савельева и И.Е. Иродова и задачниками этих же авторов, а также «Сборником качественных вопросов и задач по общей физике» Е.И. Бабаджана, В.И. Гервидса, В.М. Дубовика, Э.А. Нерсесова (М.: Наука, 1990 и М.: Физматлит, 2005). Ответ на вопрос «для чего?» сложнее. Можно высказать ту точку зрения, что подобное пособие совершенно не нужно, поскольку есть учебники и задачники. Читай учебник, решай задачи, вот и все дела. Спору нет – именно это и надо делать. Проблема, однако, в том, что большинство вчерашних школьников, а ныне первокурсников, которые окончили обычные, а не профильные физико-математические школы, задач не решали. То, что в обычной школе называют задачами, в большинстве случаев не более чем примитивные примеры на применение тех или иных формул. Такого рода упражнения мало чему могут научить, а уж показать возможности, которые даёт серьёзное научное знание, не могут в принципе. Поэтому первокурсники оказываются в довольно сложной ситуации, когда возникает необходимость решать задачи. С какого бока к ней приступать? Чем руководствоваться в процессе решения? Всё это серьёзные вопросы, на которые зачастую нет ответа в учебнике. Разумеется, есть практические занятия, где именно этому и учат, но вот пособий, помогающих студентам в их самостоятельной работе, в настоящее время мало. Именно в силу этих обстоятельств написано это пособие. Почему задача "не решается"? Понять и освоить новое знание можно только в процессе его применения. Во время учёбы такая практика возможна, в первую очередь, при решении задач. Но она не всеми студентами выполняется легко. Причин тому несколько. Первая причина – плохое знание основных понятий и законов физики или незнание их. При таких условиях все попытки решить даже простейшую задачу заранее обречены на неуспех. Это почти то же самое, что пытаться говорить в чужой стране, не зная языка, а определения и законы – язык любой науки, в том числе и физики. Вторая причина – неясность задания. Очень часто студент начинает решать задачу, даже не прочитав толком её условия. Поэтому он оказывается в положении героя сказки, получившего задание: "Пойди туда – не знаю куда, принеси то – не знаю, что". Но сказочному герою помогали чудеса, а в жизни чудес, увы, нет. Не происходит их и в этом случае. А посему напрашивается вывод: нужно внимательно прочитать условие задачи, выяснить, что дано и что необходимо найти. После этого надо КРАТКО записать условие задачи. Это – очень важный момент, поскольку необходимо внимательно прочесть задачу и ухватить её суть. Поэтому есть надежда, что при краткой записи условия оно будет прочитано достаточно внимательно, и вы будете решать ту задачу, которую вам предложили, а не ту, чаще всего некорректную, задачу, которую вы сами себе задали в результате неправильного понимания условия. Третья причина – попытка решать задачу не в общем виде (буквенном), а сразу же, используя конкретные числовые данные задачи. В этом случае любая арифметическая ошибка сильно портит все дело, и главное, что очень трудно ее обнаружить. Решение задачи в общем виде легче проконтролировать на каждом этапе и отыскать допущенную ошибку. Четвертая причина – попытка решать задачу, не изобразив на бумаге соответствующего рисунка. Конечно, можно что-то представить в уме, но рисунок неимоверно нагляднее: подсчитано, что 95 % информации человек получает с помощью глаз. Поэтому надо по возможности изобразить условие задачи с помощью рисунка, даже если вам он кажется необязательным. Пятая причина – к сожалению, наиболее трудно устранимая. Это плохое знание математики. Физика – наука точная, т.е. выводы ее основаны на использовании математики, поэтому изучение физики без знания математики – пустая трата времени. Следовательно, нужно уметь: выполнять операции с векторами, находить пределы, строить графики, дифференцировать, интегрировать и т.п. Перечисленные причины самые типичные, но могут быть и другие, сугубо индивидуальные. "А в учебнике этого нет!" Допустим, все причины, мешающие решить задачу, как будто устранены, а задача не решается. Как быть? Выход один: еще раз прочитать соответствующий раздел в учебнике, видимо, вы что-то не поняли. Кстати, нужный ли раздел вы читаете? Для ответа на этот вопрос посмотрите оглавление и предметный указатель. Очень часто случается, что вы ищете ответ совсем не там, где он находится. Бывает, что чего-то нужного вам в этом учебнике и в самом деле нет, тогда возьмите другой учебник. Вообще, лучше всего иметь под рукой несколько разных учебников и выбирать из них лучший, на ваш взгляд. К сожалению, не все учебники хороши, во многих из них имеются неточности, а иной раз и ошибки. Всё бывает. Особенно грешат этим справочники по физике для школьников и студентов. За одним, правда, исключением. Я имею в виду энциклопедии. Применительно к физике – это «Физический энциклопедический словарь» – великолепное по качеству издание, в котором всё написано правильно. Удивляться тут нечему: каждая статья в энциклопедии пишется авторитетным профессионалом физиком. Ну, а если уж ответа в учебнике или энциклопедии не нашлось, есть еще несколько выходов: подумать самому (а это весьма полезное дело!), спросить у товарища или преподавателя. В этом последнем случае чаще всего выясняется, что в книгах что-то все-таки написано, просто вы не сумели прочитать это место надлежащим образом. Вообще, чтение учебника – это не простое дело, учиться ему нужно постоянно, и чем раньше вы этому научитесь, тем легче будет учиться. Но всегда следует иметь в виду простую истину: нет такой книги, где были бы ответы на все возникающие у вас вопросы. Ответ нужно искать самому, книга может лишь помочь в этих поисках, но никогда не избавит от них. Одним словом, думайте сами! Предварительные замечания. Обычно, начиная изучать механику, многие студенты исходят из мнения, что это очень простая наука, решать задачи по механике можно, используя лишь свой житейский опыт, а основные понятия, о которых что-то твердит преподаватель на лекциях, лишь малосущественное дополнение к этому житейскому опыту. Естественно, "суровая действительность" текущих занятий, контрольных, зачетов и экзаменов заставляет многих отказаться от этого мнения и впасть в другую крайность, которая тоже далека от истины. Поэтому следует сразу же принять к сведению, что наши житейские представления зачастую имеют весьма мало общего с научными представлениями и не могут служить надежной основой для изучения точных наук. Начинать изучение механики следует с твердого усвоения основных ее понятий, если угодно, даже заучивания их. Да, заучивания! Не надо этого стесняться. Классической (ньютоновской) механике, более трёхсот лет. За это немалое время формулировки определений, законов, принципов и т.п. полностью отработаны, и трудно себе представить, что студенту, только начинающему её серьёзное изучение, придет в голову что-то полезное новое. Начните с того, что выучите их, когда придет достаточно глубокое их понимание, придёт автоматически и способность грамотно изложить их своими словами. Естественно, что такая способность только приветствуется. ЗАКОНЫ НЬЮТОНА
При решении задач этого раздела следует руководствоваться основными положениями. 1. Существуют такие системы отсчёта (их называют инерциальными), в которых тело, не взаимодействующее с другими телами, движется равномерно и прямолинейно. Это утверждение носит название закона инерции, или первого закона Ньютона. В дальнейшем будут использоваться, если не оговорено особо, только инерциальные системы отсчёта. 2. Если тело взаимодействует с другими телами, то его движение уже не будет равномерным и прямолинейным. Иными словами скорость тела будет изменяться, т.е. тело будет двигаться с ускорением. 3. Всякое взаимодействия тел характеризуется силой. Ускорение тела пропорционально сумме сил, действующих на это тело: m a = SF. Это уравнение носит название второго закона Ньютона. Здесь m – масса частицы, a – вектореё ускорения, SF – векторная сумма сил, действующих на частицу со стороны других тел. Отметим здесь, что если в задаче рассматривается движение нескольких тел, то для каждого из них необходимо записать своё уравнение второго закона Ньютона. При этом система отсчёта может быть выбрана одной для всей системы тел, а можно для каждого тела выбирать свою систему отсчёта.
4. При соприкосновении тел между ними возникают силы, приложенные в точке их соприкосновения, эти силы носят название сил реакции поверхностей. Силы реакции, если поверхности гладкие, направлены перпендикулярно поверхностям соприкасающихся тел, или, более строго, силы реакции направлены перпендикулярно касательной плоскости, проходящей через точку касания тел (рис. 2.1). 5. Если поверхности шероховатые, то сила реакции уже не будет перпендикулярна касательной плоскости. Её компонента, параллельная касательной плоскости, называется силой трения. Причем сила трения возникает либо при попытке сдвинуть одно тело по отношению к другому, либо при скольжении одного тела по поверхности другого. Следует различать два случая, когда встречается сила трения. Рассмотрим тело, находящееся на горизонтальной поверхности. Пусть к телу приложена сила F, направленная горизонтально. Случай 1. Тело покоится относительно поверхности. Тогда сумма сил, приложенных к телу, равна нулю. Спроецировав силы, действующие на тело, на вертикальное и горизонтальное направление, получим, что сила тяжести уравновешивается нормальной составляющей силы реакции поверхности. А горизонтальная составляющая силы реакции, т.е. сила трения покоя, равна по величине и противоположна по направлению внешней силе F, направленной вдоль поверхности, на которой находится тело. Сказанное иллюстрируется рис. 2.2, на котором
Случай 2. Тело скользит по поверхности. В этом случае сила трения называется силой трения скольжения
где N – величина нормальной составляющей силы реакции поверхности, k – коэффициент трения между телом и поверхностью. Считается также, что:
6. Силы взаимодействия между телами равны по величине, противоположны по направлению и действуют вдоль одной прямой (третий закон Ньютона). Задача 2.1. На горизонтальном столе находятся два бруска с массами m 1 и m 2, связанные невесомой, нерастяжимой нитью. Брусок m 1 тянут с силой F, направленной параллельно столу. Коэффициент трения между брусками и столом – k. Найти ускорение, с которым движутся бруски и силу натяжения нити, связывающей их. Решение. На рис. 2.3 изображены силы, действующие на каждое из тел. Так как нить предполагается нерастяжимой, то тела движутся с одинаковыми скоростями и, следовательно, с одинаковыми ускорениями. Составим уравнения второго закона Ньютона для каждого тела: m 1 a = F + T 1 + F тр1 + N 1 + m 1 g,(1) m 2 a = T 2 + F тр2 + N 2 + m 2 g. (2)
Рис. 2.3
Выберем систему координат XOY так, чтобы ось ОХ была направлена горизонтально, а ось OY – вертикально. Записывая (1) и (2) в проекциях на ОХ и OY, получаем: m 1 ax = F – T 1 – F тр1,(3) 0 = N 1 – m 1 g,(4) m 2 a = T 2 – F тр2,(5) 0 = N 2 – m 2 g. (6) Мы получили четыре уравнения для семи неизвестных: ах, T 1, Т 2, N 1, N 2, F тр1, F тр2. Для того чтобы эта система имела единственное решение, необходимы еще три уравнения. Первое из этих трех уравнений получим, если помимо нерастяжимости нити учтем еще и её невесомость. Так как нить нерастяжима, то ее ускорение равно ускорению тел, которые она соединяет. Тогда уравнение второго закона Ньютона для нити имеет вид: m н ax = T 1 – T 2, где m н – масса нити, T 1и T 2 – силы, приложенные к нити со стороны первого и второго тел соответственно. Так как нить невесома, то m н = 0 и T 1 – T 2 = 0, т.е. T 1 = T 2. Иными словами, нерастяжимая невесомая нить действует с одинаковыми силами на тела, которые она соединяет. Причем силы эти направлены вдоль нити. В дальнейшем мы этот результат будем постоянно использовать и не делать различия между T 1и T 2, обозначая их одной буквой, скажем, Т. Равенство T 1 = T 2 одно из трех недостающих уравнений. Нам нужны еще два уравнения. Для их получения рассмотрим силы трения. Возможны, очевидно, два случая. Случай 1. Тела движутся, поэтому: F тр1 = kN 1, F тр2 = kN 2. Тогда с учетом этих соотношений имеем вместо (3)–(6) следующую систему уравнений: m 1 ax = F – T – km 1 g,(7) m 2 ax = T – km 2 g. (8) Складывая эти уравнения, получим: (m 1+ m 2) ax = F – k (m 1+ m 2) g, откуда находим ускорение:
Затем из второго уравнения этой системы найдем Т: T =m 2 ax + km 2 g, подставляя сюда ах из (9), получим:
Проанализируем полученное выражение для ах. Это следует делать всегда, но особенно в тех случаях, когда результат не является знакопостоянной величиной (т.е. в нём где-то содержится разность некоторых величин). Так как результат для ах получен в предположении, что тела движутся, то очевидно, что ах должно быть положительной величиной:
откуда F > kg (m 1+ m 2). Если же это неравенство нарушается, т.е. F < kg (m 1+ m 2), то тела, очевидно, покоятся. Рассмотрим этот случай. Случай 2. Тела покоятся, поэтому ах = 0. Из (3)–(6) получаем тогда 0 = F – T – F тр1, 0 = T – F тр2, Если F < km 1 g, то сила F уравновешена одной лишь силой трения покоя T = F – F тр1 = 0, F тр2 = 0. Если увеличивать F, то будет возрастать и сила трения kg (m 1+ m 2) > F > km 1 g, то F тр1= km 1 g,и тогда находим T = F – km 1 g < km 2 g, F тр2 = Т< km 2 g. Задача 2.2. На наклонной плоскости, образующей угол a с горизонтом находится тело массы m 1, соединенное невесомой нерастяжимой нитью с телом массы m 2. Нить перекинута через невесомый блок. Трения в блоке нет. Коэффициент трения между телом и плоскостью равен k. Найти ускорение, с которым движутся тела. Решение. Изобразим силы, действующие на тела, предполагая, что m 1 опускается, а m 2 поднимается (рис. 2.4). Тогда сила трения направлена навстречу движению тела m 1, т.е. вверх вдоль плоскости.
Рис. 2.4
Так как нить невесома и нерастяжима, ускорения обоих тел одинаковы, а сила натяжения нити одинакова вдоль всей длины нити (см. задачу 2.1). Вводя систему координат X 1 OY 1 с осью ОХ 1, направленной вниз параллельно плоскости, напишем уравнения второго закона Ньютона для m 1 в проекциях на оси ОХ 1и OY 1: m 1 a = m 1 g× sin a – T – F тр, (1) 0 = m 1 g× cos a – N. (2) Для второго тела удобно выбрать другую систему координат, такую, что ось OX 2 направлена горизонтально, а ось OY 2 направлена вертикально вверх. Тогда для т 2 а в проекции на ось OY 2: m 2 a = T – m 2 g. (3) Уравнения (1)–(3) составляют систему трех уравнений для четырех неизвестных a, T, N, F тр. Для получения однозначного решения требуется еще одно уравнение. Так как мы предполагаем, что тела движутся, то сила трения связана с нормальной компонентой силы реакции соотношением F тр = kN. Это и есть четвёртое уравнение. Итак, имеем: m 1 a = m 1 g× sin a – T – kN, 0 = m 1 g× cos a – N, m 2 a = T – m 2 g. Согласно второму уравнению системы N = m 1 g cosa. Подставляя найденное N в первое уравнение этой системы, и складывая первое и третье уравнения, получим (m 1+ m 2) a = m 1 g sina – m 2 g – km 1 g cos a. Откуда найдём величину ускорения
Так как мы получили ответ, предполагая, что тела движутся в положительных направлениях осей ОХ 1 и OY 2, то а > 0, откуда m 1 (sina – k cos a) > m 2. (5) Подчеркнем, что полученное неравенство – условие того, что m 1 опускается. Рассмотрим теперь обратный случай, когда m 1 поднимается. Направления сил и координатных осей для этого случая изображены на рис. 2.5.
Рис. 2.5 Записывая уравнения второго закона Ньютона для тел m 1 и m 2, получим m 1 a = m 1 g× sin a – T – kN, 0 = m 1 g× cos a – N, m 2 a = T – m 2 g. Решая эту систему, найдём ускорение тел:
Опять, требуя а > 0, получим условие того, что m 1 поднимается: m 1 (sina + k cos a) < m 2. Итак: если m 1 (sina – k cos a) > m 2 – тело m 1 опускается, если m 1 (sina + k cos a) < m 2 – тело m 1 поднимается. Ясно, что если нарушены оба эти условия, т.е.: m 1 (sina – k cos a) < m 2 < m 1 (sina + k cos a), (7) то m 1 не будет ни подниматься, ни опускаться, т.е. при выполнении условия (7) тела будут покоиться. Заметим еще, что неравенство (5) имеет смысл лишь в случае, если sina – k cos a > 0, т.е: tg a > k. (8) Неравенство (8) – это условие того, что m 1 вообще может опускаться. Если (8) нарушается, то даже при m 2 = 0 тело m 1 опускаться не будет, оно будет покоиться. Задача 2.3. На гладком (трения нет) клине с углом наклона a, основание которого горизонтально, находится небольшое тело. С каким ускорением в горизонтальном направлении следует перемещать клин, чтобы тело покоилось относительно клина? Решение. Так как тело относительно клина покоится, а клин движется в горизонтальном направлении с ускорением а, то и тело движется вместе с клином с тем же ускорением в горизонтальном направлении. Согласно второму закону Ньютона: m a = m g + N. (1)
Здесь N – вся сила реакции клина, поскольку трение по условию отсутствует. Кроме силы тяжести m g и нормальной компоненты реакции опоры N на тело больше никакие силы не действуют. Выберем систему координат XOY с горизонтально направленной осью ОХ (рис. 2.6). Проецируя (1) на ОХ и OY, получим: ma = N ×sina, 0 = N ×cosa – mg. Исключая N из этой системы уравнений, получим: ma = ma ×tg a, или a = g ×tg a. Задача 2.4. На краю горизонтального диска радиуса R находится небольшое тело. Коэффициент трения между телом и диском равен k. Диск вращается с угловой скоростью w. При каком значении w тело соскользнет с диска? Решение. Так как тело движется вместе с диском, то его траектория является окружностью радиуса R. Поскольку угловая скорость w = const, то и скорость тела υ = w× R = const, и, следовательно, его тангенциальное ускорение a t = dυ / dt = 0. Таким образом, ускорение a тела равно нормальному ускорению, которое всегда направлено к центру диска и равно
Рассмотрим силы, действующие на тело (рис. 2.7). Их две: сила тяжести m g и сила реакции диска R, которую мы, как всегда, представим в виде векторной суммы её нормальной компоненты и силы трения: R = N + F тр. Согласно второму закону Ньютона: m a = m g + R. Спроецировав это уравнение на ось вращения, получим N – mg = 0, а спроецировав на направление ускорения тела, получим тап = F тр. То есть сила трения направлена к оси вращения диска и ее модуль: F тр = m w2 R. Так как тело покоится относительно диска, то F тр – сила трения покоя и потому: F тр < kN. Но N = mg,следовательно: m w2 R < k × mg, или w2< kg / R. Если это условие выполняется, то тело по диску не скользит, если же нарушается, то начинается скольжение тела по диску. Итак, тело соскользнет с диска, если w2 > kg / R. Задача 2.5. Через невесомый блок, прикреплённый к потолку, перекинута невесомая нерастяжимая верёвка. К одному концу верёвки прикреплён груз массы m, а за другой конец ухватилась обезьяна такой же массы. Сначала система находится в покое, но в некоторый момент обезьяна начинает карабкаться вверх по верёвке. На какое расстояние относительно земли переместятся обезьяна и уравновешивающий её груз, если обезьяна переместилась по верёвке на расстояние L?
Решение. На обезьяну действуют две силы (рис. 2.8): тяжести и сила реакции верёвки. То же самое относится и к грузу. Если обозначить a 1 и a 2 ускорения соответственно обезьяны и груза, то для них можно записать уравнения второго закона Ньютона: m a 1 = T + m g, m a 2 = T + m g. Здесь учтено то обстоятельство, что невесомая верёвка действует с одинаковыми силами на соединённые с нею тела. Из написанных уравнений следует, что ускорения обезьяны и груза одинаковы. Следовательно, скорости и перемещения их также одинаковы. Пусть груз поднялся на высоту h. При этом противоположный конец верёвки опустился на высоту h. Обезьяна же, как и груз, поднялась относительно земли на ту же высоту h. Значит, она оказалась на расстоянии 2 h от своего конца верёвки. Но согласно условию задачи это расстояние равно L, поэтому L = 2 h. Откуда h =L /2. Задача 2.6. Через неподвижный блок перекинута верёвка, к одному из концов которой привязан груз массой m. С какой силой необходимо тянуть второй конец верёвки, чтобы груз начал подниматься? Коэффициент трения между верёвкой и поверхностью блока k. Как изменится ответ, если верёвку обмотать вокруг блока несколько раз? Верёвку считать невесомой и нерастяжимой. Решение. Пусть верёвка скользит по блоку с постоянной скоростью. Тогда сила натяжения верёвки на конце, к которому привязан груз, равна силе тяжести, действующей на груз. Рассмотрим небольшой участок верёвки, концы которого видны под углом d j из центра блока (рис. 2.9). На этот участок действуют четыре силы: нормальная составляющая d N – силы реакции блока, d F тр – сила трения, Т и Т ' – силы натяжения верёвки, приложенные к противоположным сторонам выделенного участка. Поскольку верёвка невесома, то сумма указанных сил равна нулю. Проецируя силы на направления касательной к блоку (ось X) и радиальное направление (ось Y), получим систему уравнений:
Обозначая dT = Т'– Т и учитывая, что сила трения скольжения dF тр = kdN, получим систему уравнений:
откуда Интегрируя обе части этого уравнения, найдём ln T = k j + C. Здесь С – постоянная интегрирования. Она находится из начальных условий: Т = mg при j = 0. Отсюда находим С = ln(mg), и силу натяжения Если верёвка накинута только сверху на блок, как это изображено на рис. 2.9, то сила натяжения на втором свободном конце верёвки согласно полученному результату равна (j = p):
Если же верёвка обмотана вокруг блока n раз, то угол j = = p + 2p n, откуда
Как видим, сила, необходимая для того, чтобы верёвка начала скользить по блоку, очень быстро возрастает с увеличением числа витков верёвки вокруг блока. Реально это означает, что, намотав даже небольшое число витков вокруг блока, вы не сможете сдвинуть верёвку с места, так велика будет необходимая для этого сила. Задача 2.7. Материальная точка m находится внутри тонкого сферического слоя. Доказать, что сила тяготения, действующая на эту материальную точку со стороны слоя, равна нулю.
Решение. Для доказательства разобьём всю поверхность сферы на пары малых площадок так, чтобы каждая пара была образована пересечением конического пучка прямых, проходящих через точку т, как это изображено на рис. 2.10. Силы, с которыми притягивается точка т к получившимся площадкам, пропорциональна массам этих площадок dМ 1 и dМ 2 и обратно пропорциональна квадратам расстояний r 1 и r 2до этих площадок. Но, в свою очередь, массы площадок пропорциональны их площадям: dМ 1 = s ds 1 и dМ 2 = s ds 2, поэтому
Здесь s – масса сферического слоя, приходящаяся на единицу его площади. Проведём из центра сферического слоя радиусы к площадкам dS 1 и dS 2. Треугольник, образованный этими радиусами и отрезок, соединяющий их концы, является равнобедренным. Пусть a – угол при основании этого треугольника. Спроецируем площадки dS 1 и dS 2 на направление перпендикулярное прямой, соединяющей эти площадки. Площади этих проекций, как нетрудно понять (рис. 2.10), равны dS 1' = dS 1×cosa и dS 2' = dS 2×cosa. (2) С другой стороны, согласно определению телесного угла, телесный угол d W, в пределах которого из точки т видны обе эти площадки, можно записать по-разному:
Полученное соотношение совместно с (1) и (2) показывает, силы dF 1и dF 2 равны. Но это утверждение справедливо для каждой пары таких площадок, поэтому и весь сферический слой не оказывает никакого воздействия на материальную точку, находящуюся внутри него. Из полученного нами результата следует, что и слой конечной толщины также не оказывает никакого воздействия на материальную точку, находящуюся внутри него, поскольку такой слой можно разбить на множество тонких слоёв, каждый из которых не действует на точку, находящуюся внутри него. Задача 2.8. Оценить давление в центре Земли. Радиус Земли принять равным R= 6400 км, а среднюю плотность Земли – r = = 5,5×103 кг/м3.
Решение. Выделим мысленно объём в виде слоя толщиной dr и площадью поперечного сечения D S. Пусть эта частица находится на расстоянии r от центра Земли. Частица притягивается к центру Земли, поэтому, для того чтобы она находилась в равновесии, необходимо силу притяжения уравновесить разностью давлений:
Разобьём Землю на две части – шар, радиуса r, и сферический слой над ним (рис. 2.11, на котором шар залит серым цветом, а слой закрашен точками). Согласно результату предыдущей задачи, сила притяжения, действующая на частицу, равна силе, с которой частица притягивается к шару радиуса r, а та часть земного шара, которая находится на расстояниях превышающих r, не оказывает на частицу никакого влияния. Тогда сила притяжения легко находится. Действительно, если масса шара радиуса r равна М (r), то сила притяжения частицы массой dm к этому шару равна
Этот результат можно записать в более простом виде, если умножить и поделить его на куб радиуса Земли:
Здесь М – масса Земли, и кроме того, мы использовали то обстоятельство, что ускорение свободного падения на поверхности Земли можно записать как
Уравнение (1) с учётом (2) приобретёт вид:
Поскольку dm= rD S × dr, и p (r+dr) – p (r) = dp, то после сокращения на D S приходим к уравнению Интегрируя это уравнение по dr от 0 до R, и полагая давление на поверхности Земли равным нулю, получим Подставляя сюда числовые параметры, найдём давление в центре Земли: р» 1,8×1011 Па = 1,8×106 атм. ИМПУЛЬС
При решении задач на эту тему необходимо помнить основные положения. 1. Импульс точки p = m v, где m – масса точки, v – вектор ее скорости. 2. Импульс частицы изменяется под действием сил, приложенных к этой частице:
где 3. Импульс аддитивен, т.е. импульс системы точек равен векторной сумме импульсов точек, составляющих систему:
где p i – импульсы точек, составляющих систему, N – здесь и далее число точек в системе. 4. Замкнутой системой тел называют такую систему тел, на которую не действуют внешние силы. Импульс замкнутой системы тел не изменяется со временем. Это утверждение называется законом сохранения импульса. 5. Из третьего закона Ньютона вытекает, что сумма сил, действующих между телами замкнутой системы, равна нулю. Эти силы обычно называют внутренними силами. 6. Из пп. 3–5 вытекает уравнение:
где P – импульс системы точек, 7. Центром инерции (центром масс) системы точек называется точка, радиус-вектор которой R ци определяется следующим образом:
где r i – радиус-векторы точек с массами mi соответственно. 8. Скорость центра инерции V циопределяется как
где v i – векторы скорости точек с массами mi соответственно, Р – импульс системы точек, M – сумма масс точек, составляющих систему (масса системы). Это равенство можно записать иначе: Р = М V ци, т.е. импульс системы материальных точек совпадает с импульсом материальной точки, масса которой равна массе системы точек, а скорость равна скорости центра масс системы. 9. Дифференцируя последнее уравнение по времени и воспользовавшись уравнением п. 6, найдём ускорение a ц центра инерции:
где М – масса системы, Задача 3.1. Из автомата, выпускающего n пуль в секунду, производится стрельба по стальной плите. При ударе о плиту пуля полностью теряет свою скорость. Найти среднюю силу, действующую на плиту, если масса каждой пули m, а скорость υ, причем пули летят перпендикулярно поверхности плиты. Решение. Согласно второму закону Ньютона d p / dt = F. Таким образом, средняя сила, действующая на плиту, равна импульсу, переданному за одну секунду плите, ударившимися о неё пулями. Так как число таких пуль равно n и импульс каждой из них р = m v, то сила равна: F = nm v. Для автомата примем числовые значения: m = 7 г, υ = 500 м/с, п = 10 с–1. Тогда: F = 7×10–3×500×10 = 35 Н. Подумайте сами, как изменится ответ, если пули упруго рикошетируют от плиты, т.е. после удара их скорость имеет прежнюю величину, но направление движения изменяется на обратное. Кстати, вот ещё какой вопрос: а как обстоит дело со знанием физики у творцов современных боевиков, в которых мы частенько видим, как пули, попадающие в злодея, буквально сносят его? Задача 3.2. Найти положение центра инерции следующих систем: 1) двух материальных точек, находящихся на некотором расстоя
|
||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.178.145 (0.012 с.) |

 Рис. 2.1
Рис. 2.1
 .
. Рис. 2.2
Рис. 2.2
 . Она направлена в сторону, противоположную направлению движения тела и равна по величине
. Она направлена в сторону, противоположную направлению движения тела и равна по величине ,
,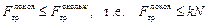 .
.
 . (9)
. (9) . (10)
. (10) ,
, < km 1 g. Но тогда
< km 1 g. Но тогда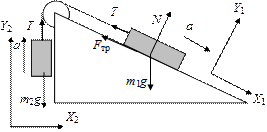
 (4)
(4)
 (6)
(6)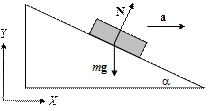 Рис. 2.6
Рис. 2.6
 .
. Рис. 2.7
Рис. 2.7
 Рис. 2.8
Рис. 2.8

 Рис. 2.9
Рис. 2.9


 .
. .
. .
. Рис. 2.10
Рис. 2.10
 (1)
(1) .
. Рис. 2.11
Рис. 2.11
 . (1)
. (1) (2)
(2) .
.
 .
.


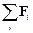 – сумма сил, приложенных к частице. Это просто иная, причем наиболее общая, формулировка второго закона Ньютона.
– сумма сил, приложенных к частице. Это просто иная, причем наиболее общая, формулировка второго закона Ньютона.

 – силы, действующие на тела системы, со стороны тел, не входящих в систему (такие силы называют внешними силами). Так, при взрыве летящего снаряда, силы, разрывающие снаряд, являются внутренними силами по отношению к снаряду, а сила тяжести является внешней силой.
– силы, действующие на тела системы, со стороны тел, не входящих в систему (такие силы называют внешними силами). Так, при взрыве летящего снаряда, силы, разрывающие снаряд, являются внутренними силами по отношению к снаряду, а сила тяжести является внешней силой. ,
, ,
,



