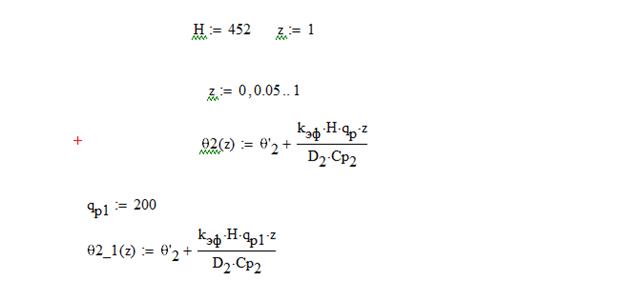Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение для теплопередающей стенки труб.Содержание книги
Поиск на нашем сайте
6.1. РП-модель:
При выводе уравнения энергии распределённой модели в линейном приближении можно принять допущения о постоянстве свойств теплопередающей стенки (
общее решение уравнения:
Примем следующие граничные условия - температура теплоносителя Нахождения
где Передаточная функция по каналу θ2→υ для РТО:
6.2. СП-модель:
Модель плоской стенки точечного приближения, дающей равенство температур при любом y можно получить лишь при допущении
Тогда из уравнения Фурье:
Уравнение теплопроводности для радиационного теплообменника принимает вид:
Где
Передаточная функция по каналу θ2→υ:
График 6 -КЧХ стенки по каналу стенки по каналу
При y=0 температура Коэффициенты усиления всех моделей одинаковы и равны единице. Инерционность температуры наружной поверхности больше инерционности внутренней поверхности.
График 7-КЧХ стенки по каналу стенки по каналу
График 8 -КЧХ стенки по каналу стенки по каналу
График 9 -КЧХ стенки по каналу стенки по каналу
Различия между СП- и РП-моделями будет тем меньше, чем меньше коэффициент теплоотдачи Годографы с уменьшением значений На графике представлены КЧХ СП модели, и КЧХ РП модели внутри и снаружи стенки. В области низких частот модели имеют одинаковый коэффициент усиления 1, однако с ростом частоты расхождение сначала увеличивается, а затем снова уменьшается. Это означает, что СП-модель мы можем использовать только для статических моделей или для динамических на низких частотах. В динамике она дает большие отклонения на средних и высоких частотах, поэтому не применима.
Модель статики объекта
Статика. РП-модель:
Особенностью моделирования радиационных теплообменников является возможность принимать допущение о независимости величины радиационного потока от температуры наружной поверхности стенки Для определения распределения температуры Исходное уравнение энергии внутреннего теплоносителя:
С граничными условиями:
В статике тепловой поток внутри плоской стенки постоянен по координате y.
После интегрирования уравнения получим искомую зависимость для распределения температуры внутреннего теплоносителя в статике
Так же из уравнения энергии получим распределение по длине температуры наружного теплоносителя
Рисунок 4- Распределение по длине трубы температур внутреннего теплоносителя, внутренней поверхности стенки и наружной поверхности стенки для РП-модели
Температуры внутреннего теплоносителя, внутренней поверхности стенки и наружной поверхности стенки по длине возрастает.
CП-модель
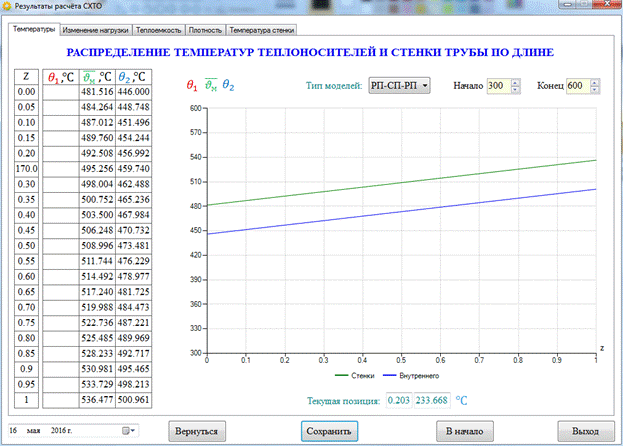
Рисунок 5 - Распределение по длине трубы температур внутреннего теплоносителя и внутренней поверхности стенки для СП-модели
Глядя на график можно сделать вывод, что по длине температура стенки трубы и теплоносителя увеличивается пропорционально. При рассмотрении только СП-модели и более точной РП модели, обнаружили, что изменение разницы температур на выходе из теплообменника составила 36 градусов Цельсия.
График 10 - Распределение по длине трубы температур внутреннего теплоносителя и внутренней поверхности стенки для СП-модели
Вывод: при увеличении плотности потока излучения в 2 раза увеличивается изменение температуры второго теплоносителя.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.005 с.) |

 ). Запишем в приращениях относительно стационарного режима:
). Запишем в приращениях относительно стационарного режима: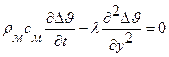 .
.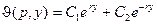 .
. для внутренней поверхности и удельный тепловой поток
для внутренней поверхности и удельный тепловой поток  для наружной поверхности. (стр.71).
для наружной поверхности. (стр.71). из граничных условий третьего рода - значения температуры наружного и внутреннего теплоносителя. Решение находится по уравнению Фурье. В результате получаем:
из граничных условий третьего рода - значения температуры наружного и внутреннего теплоносителя. Решение находится по уравнению Фурье. В результате получаем: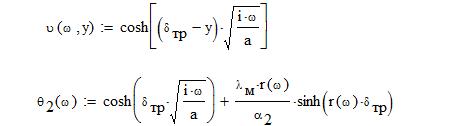
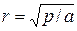 ,
,  - коэффициент температуропроводности стенки.
- коэффициент температуропроводности стенки.
 , т.е об отсутствии теплового сопротивления стенки.
, т.е об отсутствии теплового сопротивления стенки. .
.


 - постоянная времени металла стенки
- постоянная времени металла стенки

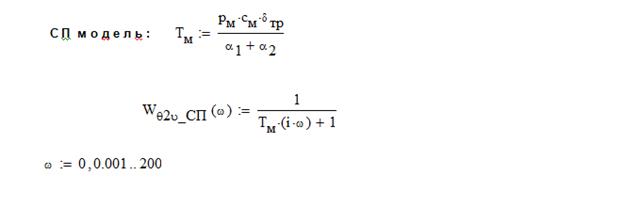
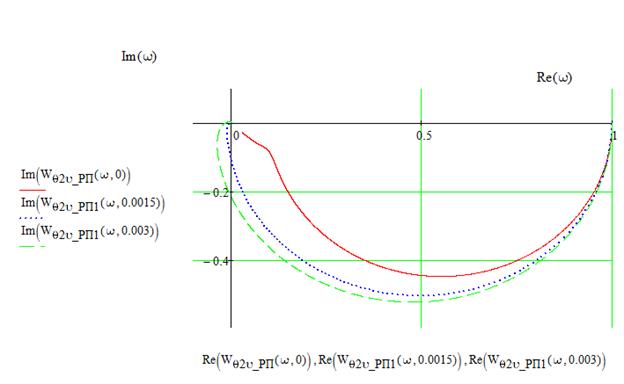
 РП – модели для различной толщины стенки трубы
РП – модели для различной толщины стенки трубы на внутренней поверхности стенки, для
на внутренней поверхности стенки, для 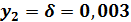 температура
температура  наружной поверхности стенки при возмущении по температуре потока
наружной поверхности стенки при возмущении по температуре потока 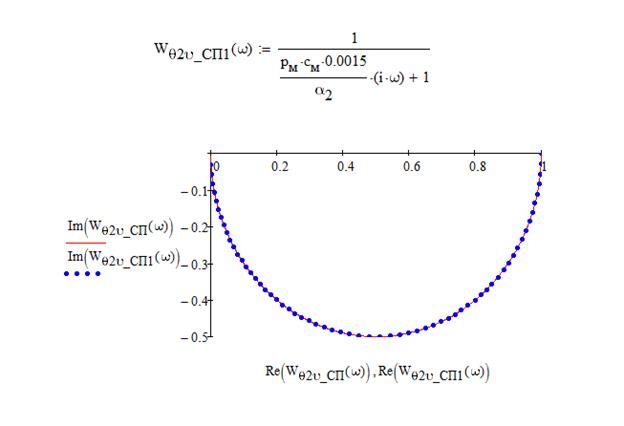




 и толщина стенки
и толщина стенки 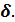

 в силу большого различия четвертых степеней температур наружного теплоносителя и стенки в уравнении Стефана-Больцмана.
в силу большого различия четвертых степеней температур наружного теплоносителя и стенки в уравнении Стефана-Больцмана. достаточно рассмотреть уравнения энергии внутреннего теплоносителя и стенки:
достаточно рассмотреть уравнения энергии внутреннего теплоносителя и стенки:
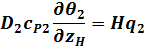

 =
= 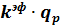
 =
=