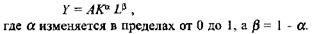Производственная функция Кобба-Дугласа и ее свойства

Функция Кобба-Дугласа получена в результате математического преоб­разования простейшей производственной функции У= F(L, К) в такую мо­дель, которая показывает, какой долей совокупного продукта вознагражда­ется участвующий в его создании фактор производства. Она имеет следую­щий вид:

Функция Кобба-Дугласа - модель с двумя переменными факторами производства. Параметр А - коэффициент, отражающий уровень техно­логической производительности и в краткосрочном периоде он не изме­няется. Показатели а и j3 - коэффициенты эластичности объема выпус­ка (К) по фактору производства, т. е. по капиталу К и труду L соответ­ственно. При этом, если каждый из факторов оплачивается в соответ­ствии со своим предельным продуктом, то а и /3 показывают доли капи­тала и труда в совокупном доходе. Иными словами, если цена капита­ла равна предельному продукту капитала, а цена труда равна предель­ному продукту труда, то параметры а и /3 определяют пропорцию, в ко­торой труд и капитал получают свое вознаграждение за созданный про­дукт, т. е. долю капитала в доходе a Y и долю труда в доходе /3Y. Так как /3 = 1 - α, то а + /3 = 1, из чего следует, что мы имеем дело с постоянной отдачей от масштаба. Интересно рассмотреть эмпирические значения параметров функции Кобба-Дугласа: А = 1,1; а = 1/4; /J = 3/4. Следовательно, доля капитала в национальном доходе составляет 25%, а доля тру­да - 75%.

В поисках путей наибольшей эффективности производства нас всегда должна интересовать предельная производительность участвующих в нем факторов', с помощью которой определяется оптимальный объем исполь­зуемых ресурсов. Предельный продукт капитала МР_К пропорционален от­ношению доли капитала в доходе к объему использованного капитала: МР_к = аУ / К. Аналогично определяется и предельная производительность труда: MP_L =/3Y/L.

Рассмотрим свойства производственной функции Кобба-Дугласа.

Первое свойство - постоянство отдачи от масштаба - описывается формулой F(nK,nL) = п А К°Ь ^В и означает, что если увеличить использова­ние капитала и труда в n раз, то объем совокупного выпуска, или объем до­хода, возрастет в такое же число раз.

Второе важное свойство функции Кобба-Дугласа связано с изменением предельной производительности факторов. Например, если привлечь в производство дополнительное количество капитала К, а труд L использо­вать в прежнем объеме, то, при прочих равных условиях, предельная про­изводительность труда MP _L увеличится, а предельная производительность возросшего объема капитала МР_к снизится. Если же увеличить количество труда, при прочих равных условиях, то его предельная производительность снизится, а предельная производительность капитала возрастет. Вывод: нарушение пропорции между трудом и капиталом при заданной техноло­гии приводит к отклонению от оптимального объема производства, т. е. к неэффективности производства.

 

Третье свойство производственной функции Кобба-Дугласа ~ постоян­ство отношения дохода от труда к доходу от капитала (Р/а), т. е. посто­янство соотношения долей капитала и труда в национальном продукте.

Исследования американского сенатора и экономиста Пола Дугласа по­казали, что в Соединенных Штатах за сорок лет (с 1948 по 1989 гг.) соот­ношение р / а колебалось в пределах между 2 и З², в результате чего оплата труда в 2-3 раза превышала вознаграждение капитала.¹ Можно предполо­жить, что постоянные рамки колебания соотношения |3 / а заданы техноло­гически. Колебания /5 / а внутри этих рамок могут быть объяснены откло­нением в соотношении / и S, так как вряд ли заработная плата, шкала на­логообложения и нормы амортизации почти ежегодно могли претерпевать значительные изменения.

Макроэкономическое равенство / = 5 лежит в основе механизма эконо­мического роста еще одной неоклассической модели, которая также бази­руется на производственной функции. Она называется моделью роста Со-лоу, по имени американского экономиста, лауреата Нобелевской премии Роберта Солоу.

Модель роста Солоу

Цель данной модели - ответить на три важных вопроса экономической политики: как добиться высоких и стабильных темпов роста, как одновре­менно с этим найти максимальный объем потребления и какое влияние на экономический рост оказывает увеличение населения и внедрение новых технологий.

Построение модели. Разделив двухфакторную производственную функ­цию Y = F(K,L) на количество труда L, мы получим производственную фун­кцию для одного человека: у =f(k), где к = K/L - уровень капиталовоору­женности единицы труда. Доход предстает как функция только одного фак­тора - капиталовооруженности. Такая единичная производственная функ­ция изображена на рис. 25.2.

В данной функции предельная производительность капитала МР изме­ряется постоянно меняющимся углом наклона кривой у =/(к) и показыва­ет прирост выпуска, если капиталовооруженность работника возрастет на 1 единицу, т. е. МР_К = f(k + /) -f(k).

В модели Солоу спрос на продукцию предъявляется со стороны потре­бителей и инвесторов. Производственные блага в условиях равновесия пол­ностью инвестируются (S = /), не оставляя места накоплению товарно-ма­териальных запасов. Помня о макроэкономическом равенстве Y = С + I, вы­пуск одного работника можно записать в виде у = с + i; функцию по­требления как с = (l-s)y = (l-s)f(k)², а функцию инвестиций на одного работника как i = sy = s f(k). Графически размер потребления и инвестиций при каждом уровне капиталовооруженности изображены на рис. 25.2. Ли­нией sf{k) обозначена функция инвестиций. Расстояние между функциями f(k) и sf(k) определяет объем потребления. На этом основании функция по­требления выглядит как c=f(k) - Щк).

Важное место в модели Солоу занимает рассмотрение движения капи­тальных запасов, величина которых составляет разницу между размером инвестиций и объемом выбытия капитала: Д к =/- 6 к, где 6 - норма выбы­тия капитала (или норма амортизации) и является константой, а 6 к - объем выбытия капитала.

Экономика достигает равновесия. Уро­вень капиталовооруженности, при котором Д к = 0, называется устойчи­вым уровнем капиталовооруженности (к*) и характеризует состояние равновесия экономики, отличающееся устойчивостью инвестиций и вы­бытия капитала, неизменностью объема производства. В условиях рав­новесия sf(k*) -б к* = 0 или sf(k*) = б к*.

Эта формула дает возможность вычислить устойчивый уровень капита­ловооруженности (к*), не прибегая к длительным подсчетам ежегодного прироста капитала и производства за ряд лет. Из пропорции к*// (к*) = s/6 видно, что к* =f(k*) s/6.

 

 

Неокейнсианские модели экономического роста

В неокейнсианских моделях экономический рост исследуется с помо­щью инструментов и методов анализа кейнсианской школы, примененных к динамическим процессам. Напомним, что под динамическим равновеси­ем понимается равенство темпов прироста совокупного спроса и совокуп­ного предложения. Поэтому модели, исследующие достижение и характер такого равенства, называются динамическими.

Необходимо отличать временные лаги от понятий кратко- и долгосроч­ного периода. В динамических моделях, в отличие от статических, крите­рием кратко- или долгосрочности периода является изменение технологии производства. Краткосрочный динамический период характеризуется неиз­менностью технологии, которая может сохраняться в предыдущем, теку­щем и будущем периодах (t₁, t и t) при варьирующихся темпах реального ВВП. Соответственно, в долгосрочном динамическом плане меняется сам технологический уровень производства.¹