
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия - это энергия положенияСодержание книги
Поиск на нашем сайте
: U = mgh Мощность Мощность - это скорость выполнения работы за единицу времени P = W/t (Дж/с) или (Вт) Мощность является скалярной величиной!
8.Колебания.Гармонические колебания, их основные параметры. Уравнение гармонических колебаний.
Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени.. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида
где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.
Физ.маятник – твердое тело,которое может совершать колебания относительно неподвиж.гориз.оси не проход.через центр тяж.тела M=- mgh sin A(альфа)
Мат.маятник- матер.точка подвеш.на тонкой нерастяж.нити(невесомой)
T=2gΠ
Виды деформации. Закон Гука. Модуль Юнга. Деформация -это изменение формы и размера тел под действием внешних сил. Различают два вида деформаций: упругие и пластические. Упругой деформация называется, если после прекращения действия внешних сил тело принимает первоначальную форму и размеры. Пластической деформация называется, когда тело после прекращения воздействия продолжает сокращаться Закон Гука: Величина упругой деформации пропорциональна действующей силе
Модуль Юнга - численно равен сили растягивающей стержень вдвое с единичной площадью поперечного сечения. Модуль Юнга зависит от свойств материала и не зависит от размеров и формы тела Е=
11.Гидродинамика идеальной жидкости. Уравнение неразрывности потока. Уравнение Бернулли Идеальной называется абсолютно несжимаемая жидкость, не обладающая вязкостью.
Уравнение неразрывности жидкости. Это такое движение жидкости, при котором в её потоке не возникает пустот. Для произвольных сечений элементарной струйки с площадью dS1,dS2….dSn, где жидкость течет со скоростью соответственно u1,u2…un расход жидкости одинаков: dQ1,= dQ2…=dQn Подстановка в данное выражение позволяет получить уравнение неразрывности элементарной струйки жидкости: U1 * dS1 = u2 * dS2 = …. = un * dSn = const Для потока жидкости уравнение неразрывности имеет вид: U * S = const Уравнение Бернулли Уравнение Бернулли можно вывести, используя закон сохранения энергии при описании течения жидкости в трубке. Для элементарной струйки идеальной жидкости уравнение Бернулли записывается в виде:
Где z1 z2 – геометрическая высота или геометрический напор в произвольных сечениях 1 и 2 элементарной струйки идеальной жидкости, u2 u1 – скорость элементарной струйки в сечении 1 и 2, p1 p2 – давление в сечениях 1 и 2 элементарной струйки, p – плотность жидкости.
Внутренним трением(или вязкостью) называется свойство жидкостей или газов оказывать сопротивление при перемещении одной части жидкости относительно другой. это свойство жидкостей и газов количественно характеризуется коэф.вязкости ῃ(или просто вязкостью) При движ.тела с сферич.формой в вязкой среде с малой скоростью на тело действует сила внутр.трения пропорц. Коэф.вязкости.
Ньютоновские и неньютоновские жидкости.
Жидкости, не подчиняющиеся уравнению относят к неньютоновским. Для них вязкость h зависит от скорости течения (градиента скорости dv/dx) жидкости. Такие жидкости содержат молекулы или частицы, склонные к образованию пространственных структур. Примерами неньютоновских жидкостей являются суспензии, эмульсии, растворы макромолекул (например, некоторых белков), цельная кровь. Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютоновских – аномальной.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.4 (0.01 с.) |



 Ftp=O
Ftp=O d=ƪ
d=ƪ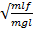

 , где К-жесткость пружины, ▲ƪ-деформация
, где К-жесткость пружины, ▲ƪ-деформация ,
, 


 , где
, где  -градиент скорости потока в данном месте,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости, а, следовательно, и поверхности соприкасающихся слоёв площадью S.
-градиент скорости потока в данном месте,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости, а, следовательно, и поверхности соприкасающихся слоёв площадью S.


