Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия тела прямо пропорциональна его массе и скорости - кинетическая энергия тем больше, чем выше скорость и больше масса тела.Содержание книги
Поиск на нашем сайте
Система отсчета. Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой. Итак, элементами системы отсчета, необходимыми для описания движений, являются: начало отсчета, масштабы отсчета расстояний, три направления отсчета положения тел, начало отсчета времени, масштаб времени. Для определения положения материальной точки в любой момент времени необходимо также задать начало отсчета времени. Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела. Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно. Путь и перемещение. Линия, по которой движется точка тела, называется траекторией движения. Длина траектории называется пройденным путем. Вектор, соединяющий начальную и конечную точки траектории, называется перемещением. Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение. Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением Поступательное и вращательное движения — самые простые примеры механического, движения тел.
2.Поступательное и вращательное движение. Скорость и ускорение при поступательном и вращательном движении. Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, перемещается параллельно сама себе.(кабина лифта). При поступательном движении все точки тела движутся одинаково, поэтому достаточно изучить движение одной какой-то произвольной точки тела (например, движение центра масс тела), так же при поступательном движении тело не изменяет ни своего вида, ни строения, одновременные скорости всех точек равны и параллельны между собой, также равны и параллельны между собой ускорения всех точек.
3.Динамика материальной точки. 1 закон Ньютона. Интегральные системы отсчета. В качестве материальных объектов в механике рассматриваются материальная точка, абсолютно твердое тело и система материальных точек или тел. Материальной точкой называется точка, обладающая массой. Абсолютно твердое тело – это материальное тело, в котором расстояния между двумя любыми точками остаются неизменными. Механической системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех остальных. Материальная точка - это модель материального тела любой формы, размерами которого в конкретной задаче можно пренебречь. Первый закон динамики (закон инерции): материальная точка при отсутствии внешних воздействий сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные к ней силы не изменят этого состояния. Законы динамики Галилея-Ньютона
4. 2 закон Ньютона. 3 закон Ньютона
Сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного и прямолинейного движения. Масса тела выступает как коэффициент пропорциональности между силой, действующей на тело, и ускорением (F = ma) и характеризует инертность тела, т. е. степень неподатливости изменению состояния движения.
Третий закон Ньютона: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки, т. е.
Выдающейся заслугой Ньютона было открытие закона всемирного тяготения: два точечных тела притягивают друг друга с силой, прямо пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними и направленной вдоль соединяющей их прямой, т. е.
где? = 6,7 10-11 м3/(кг • с2) – гравитационная постоянная; m1 и m2 – массы тел; r – расстояние между телами.
5.Момент импульса. Момент силы. Уравнение моментов.
6.Момент инеркции. Теор Штейнера. Основной закон динамики вращательного движения. Единица измерения в Международной системе единиц (СИ): кг·м². Обозначение: I или J.
Теорема Гюйгенса — Штейнера Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где m — полная масса тела.
7.Механическая работа. Кинетическая и потенциальная энергия. Мощность. Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы F на модуль перемещения
В СИ единицей работы является джоуль (Дж). Кинетическая энергия Когда сила, приложенная к телу, больше силы сопротивления, то результирующая сила приводит тело в движение. Движущееся тело обладает кинетической энергией. Работа по ускорению тела тратится на увеличение его скорости, т.е. увеличение кинетической энергии: K = 1/2(mV2) Мощность Мощность - это скорость выполнения работы за единицу времени P = W/t (Дж/с) или (Вт) Мощность является скалярной величиной!
8.Колебания.Гармонические колебания, их основные параметры. Уравнение гармонических колебаний.
Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени.. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида
где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.
Физ.маятник – твердое тело,которое может совершать колебания относительно неподвиж.гориз.оси не проход.через центр тяж.тела M=- mgh sin A(альфа)
Мат.маятник- матер.точка подвеш.на тонкой нерастяж.нити(невесомой)
T=2gΠ
Уравнение Бернулли Уравнение Бернулли можно вывести, используя закон сохранения энергии при описании течения жидкости в трубке. Для элементарной струйки идеальной жидкости уравнение Бернулли записывается в виде:
Где z1 z2 – геометрическая высота или геометрический напор в произвольных сечениях 1 и 2 элементарной струйки идеальной жидкости, u2 u1 – скорость элементарной струйки в сечении 1 и 2, p1 p2 – давление в сечениях 1 и 2 элементарной струйки, p – плотность жидкости.
Внутренним трением(или вязкостью) называется свойство жидкостей или газов оказывать сопротивление при перемещении одной части жидкости относительно другой. это свойство жидкостей и газов количественно характеризуется коэф.вязкости ῃ(или просто вязкостью) При движ.тела с сферич.формой в вязкой среде с малой скоростью на тело действует сила внутр.трения пропорц. Коэф.вязкости.
Ньютоновские и неньютоновские жидкости.
Жидкости, не подчиняющиеся уравнению относят к неньютоновским. Для них вязкость h зависит от скорости течения (градиента скорости dv/dx) жидкости. Такие жидкости содержат молекулы или частицы, склонные к образованию пространственных структур. Примерами неньютоновских жидкостей являются суспензии, эмульсии, растворы макромолекул (например, некоторых белков), цельная кровь. Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютоновских – аномальной. Число Рейнольдса. Определяет режим движения жидкости.
v-скорость потока d-диаметр трубки ню-кинематический коэффициент вязкости Если 14.Основные положения молекулярно-кинетической теории (мкт). Опыты подтверждающие мкт. Основное уравнение мкт.
Подтверждение:
p – давление
15.Поверхностный слой в жидкостях. Коэф. поверхностного натяжения. Свободная энергия поверхностного слоя жидкости. Свойства вещества в этой межфазовой поверхности, толщиной в несколько поперечников атомов или молекул, отличаются от свойств внутри объёма фазы. Внутри объёма чистого вещества в твёрдом, жидком или газообразном состоянии любая молекула окружена себе подобными молекулами. Свободная энергия поверх.слоя.жид. изменение свободной энергии прямо пропорционально изменению площади поверхности жидкости. Коэффициент поверхностного натяжения – это величина, характеризующая зависимость работы молекулярных сил, идущих на изменение площади свободной поверхности жидкости и самой площади изменения этой поверхности. σ = А/ΔS σ - коэффициент поверхностного натяжения А – работа молекулярных сил по изменению площади поверхности жидкости ΔS - изменение площади поверхности жидкости σ измеряется работой молекулярных сил при уменьшении площади свободной поверхности жидкости на единицу.зависит от рода жидкости и внешних условий, например, температуры 16.Доп.давление под искривленной поверхностью жидкости. Формула Лапласа.
17.Смачивание и несмачивание капилярные явл.Формула Борелли-Жюрена формула Борелли-Жюрена получена в 1670 г. Величина 2а/pg,входящая в правую часть формулы,назыв.капиллярной постоянной;она явл.важной физико-хим.хар-ой жидкости.
Мощность постоянного тока - отношение работы тока за время t к этому интервалу времени.
В системе СИ:
Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
где I - сила тока в цепи, R - сопротивление, t - время По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время. В системе СИ: [Q] = 1 Дж.
Система отсчета. Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой. Итак, элементами системы отсчета, необходимыми для описания движений, являются: начало отсчета, масштабы отсчета расстояний, три направления отсчета положения тел, начало отсчета времени, масштаб времени. Для определения положения материальной точки в любой момент времени необходимо также задать начало отсчета времени. Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела. Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно. Путь и перемещение. Линия, по которой движется точка тела, называется траекторией движения. Длина траектории называется пройденным путем. Вектор, соединяющий начальную и конечную точки траектории, называется перемещением. Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение. Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением Поступательное и вращательное движения — самые простые примеры механического, движения тел.
2.Поступательное и вращательное движение. Скорость и ускорение при поступательном и вращательном движении. Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, перемещается параллельно сама себе.(кабина лифта). При поступательном движении все точки тела движутся одинаково, поэтому достаточно изучить движение одной какой-то произвольной точки тела (например, движение центра масс тела), так же при поступательном движении тело не изменяет ни своего вида, ни строения, одновременные скорости всех точек равны и параллельны между собой, также равны и параллельны между собой ускорения всех точек.
3.Динамика материальной точки. 1 закон Ньютона. Интегральные системы отсчета. В качестве материальных объектов в механике рассматриваются материальная точка, абсолютно твердое тело и система материальных точек или тел. Материальной точкой называется точка, обладающая массой. Абсолютно твердое тело – это материальное тело, в котором расстояния между двумя любыми точками остаются неизменными. Механической системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех остальных. Материальная точка - это модель материального тела любой формы, размерами которого в конкретной задаче можно пренебречь. Первый закон динамики (закон инерции): материальная точка при отсутствии внешних воздействий сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные к ней силы не изменят этого состояния. Законы динамики Галилея-Ньютона
4. 2 закон Ньютона. 3 закон Ньютона
Сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного и прямолинейного движения. Масса тела выступает как коэффициент пропорциональности между силой, действующей на тело, и ускорением (F = ma) и характеризует инертность тела, т. е. степень неподатливости изменению состояния движения.
Третий закон Ньютона: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки, т. е.
Выдающейся заслугой Ньютона было открытие закона всемирного тяготения: два точечных тела притягивают друг друга с силой, прямо пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними и направленной вдоль соединяющей их прямой, т. е.
где? = 6,7 10-11 м3/(кг • с2) – гравитационная постоянная; m1 и m2 – массы тел; r – расстояние между телами.
5.Момент импульса. Момент силы. Уравнение моментов.
6.Момент инеркции. Теор Штейнера. Основной закон динамики вращательного движения. Единица измерения в Международной системе единиц (СИ): кг·м². Обозначение: I или J.
Теорема Гюйгенса — Штейнера Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где m — полная масса тела.
7.Механическая работа. Кинетическая и потенциальная энергия. Мощность. Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы F на модуль перемещения
В СИ единицей работы является джоуль (Дж). Кинетическая энергия Когда сила, приложенная к телу, больше силы сопротивления, то результирующая сила приводит тело в движение. Движущееся тело обладает кинетической энергией. Работа по ускорению тела тратится на увеличение его скорости, т.е. увеличение кинетической энергии: K = 1/2(mV2) Кинетическая энергия тела прямо пропорциональна его массе и скорости - кинетическая энергия тем больше, чем выше скорость и больше масса тела. 2. Потенциальная энергия
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.1.23 (0.011 с.) |


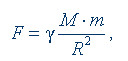
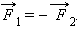


 и на косинус угла
и на косинус угла  между ними
между ними


 Ftp=O
Ftp=O d=ƪ
d=ƪ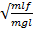


 , где
, где  -градиент скорости потока в данном месте,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости, а, следовательно, и поверхности соприкасающихся слоёв площадью S.
-градиент скорости потока в данном месте,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости, а, следовательно, и поверхности соприкасающихся слоёв площадью S.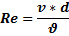
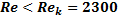 – ламинарный, если
– ламинарный, если  – турбулентный режим.
– турбулентный режим.


 пласа
пласа