
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородные оду с постоянными коэффициентами. Характеристическое уравнение. Построение общего решения по корням характеристического уравнения.Содержание книги
Поиск на нашем сайте
Для решения неоднородного линейного дифференциального уравнения с постоянными коэффициентами необходимо найти общее решение а также одно частное решение Для поиска частного решения неоднородного уравнения в случае, если Для решения неоднородного дифференциального уравнения малого порядка можно использовать метод Лагранжа (метод вариации произвольных постоянных). Пусть
Решив полученные обыкновенные дифференциальные уравнения первого порядка, получим и общее решение исходного дифференциального уравнения.
Неоднородные ОДУ с постоянными коэффициентами. Структура общего решения. Уравнение Уравнение (9.2) называется линейным однородным дифференциальным уравнением n-го порядка с постоянными коэффициентами; Уравнение
может выполняться только когда все Если фундаментальная система решений найдена, то функция дает общее решение однородного уравнения (9.2 (все с от к -константы). Фундаментальная система решений имеет вид: Функция
Метод вариации произвольных постоянных. Структура частного решения неоднородного ОДУ с постоянными коэффициентами и правой частью специального вида. Метод пригоден для линейных уравнений (с постоянными и произвольными коэффициентами), если известна фундаментальная система соответствующего однородного уравнения. Общее решение в этом случае можно найти для правой части произвольного вида (необязательно стандартного). Суть метода (метода Лагранжа) состоит в том, что общее решение ищется в виде где
Функции где Методом Лагранжа может быть решено любое неоднородное уравнение с постоянными коэффициентами. Однако если свободный член в уравнении (20) имеет вид где Pm1(x) и Qm2(x) - многочлены степеней, соответственно, m1 и m2, можно сразу указать вид частного решения в форме с неопределёнными коэффициентами. Общее правило таково: составим из коэффициентов при x в экспоненте и тригонометрических функциях число и пусть r - кратность числа s0 как корня характеристического уравнения, m= max(m1, m2). Тогда частное решение надо искать в виде, где Rm(x) и Sm(x) - многочлены степени m с
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.241.104 (0.008 с.) |


 соответствующего однородного уравнения
соответствующего однородного уравнения 
 неоднородного уравнения. Тогда общее решение неоднородного дифференциального уравнения имеет вид
неоднородного уравнения. Тогда общее решение неоднородного дифференциального уравнения имеет вид 
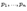 -- постоянные, можно использовать метод неопределенных коэффициентов. А именно, если является многочленом ф от х с постоянными коэффициентами, либо
-- постоянные, можно использовать метод неопределенных коэффициентов. А именно, если является многочленом ф от х с постоянными коэффициентами, либо  есть сумма или произведение указанных функций, то частное решение можно искать в таком же виде, но с другими коэффициентами, подлежащими определению. Исключение составляют особые (резонансные) случаи, когда либо 1) -- многочлен, и
есть сумма или произведение указанных функций, то частное решение можно искать в таком же виде, но с другими коэффициентами, подлежащими определению. Исключение составляют особые (резонансные) случаи, когда либо 1) -- многочлен, и  является корнем кратности характеристического уравнения, либо 2)
является корнем кратности характеристического уравнения, либо 2)  , и
, и  являются корнями кратности характеристического уравнения. В этих особых случаях частное решение отличается от правой части уравнения не только постоянными коэффициентами, то и дополнительным множителем.
являются корнями кратности характеристического уравнения. В этих особых случаях частное решение отличается от правой части уравнения не только постоянными коэффициентами, то и дополнительным множителем. и
и  -- независимые частные решения уравнения
-- независимые частные решения уравнения  . Тогда решение уравнения
. Тогда решение уравнения  по методу Лагранжа находится в виде
по методу Лагранжа находится в виде 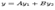 , где а и б -- функции от х, удовлетворяющие системе дифференциальных уравнений:
, где а и б -- функции от х, удовлетворяющие системе дифференциальных уравнений: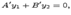
 Следовательно,
Следовательно, 
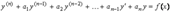 (9.1) называется линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами;
(9.1) называется линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами;  - постоянные вещественные числа. Если функция
- постоянные вещественные числа. Если функция  ) не равна тождественно нулю, то иногда говорят, что уравнение с правой частью.
) не равна тождественно нулю, то иногда говорят, что уравнение с правой частью.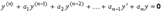
 - постоянные вещественные числа. Т. к. функция ф от х) равна тождественно нулю, то иногда говорят, что уравнение без правой части.
- постоянные вещественные числа. Т. к. функция ф от х) равна тождественно нулю, то иногда говорят, что уравнение без правой части. (9.3) называется характеристическим уравнением, а его корни – характеристическими числами уравнения (9.2). Система функций
(9.3) называется характеристическим уравнением, а его корни – характеристическими числами уравнения (9.2). Система функций 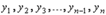 называется линейно независимой в интервале а -б если тождество(
называется линейно независимой в интервале а -б если тождество( - постоянные числа)
- постоянные числа) 
 . Если к тому же каждая из функций
. Если к тому же каждая из функций  является частным решением однородного уравнения (9.2), то система решений одно-родного уравнения называется фундаментальной системой решений.
является частным решением однородного уравнения (9.2), то система решений одно-родного уравнения называется фундаментальной системой решений.

 дает общее решение однородного уравнения (9.2) (все с от к - константы).
дает общее решение однородного уравнения (9.2) (все с от к - константы).
 - непрерывно дифференцируемые функции от x;
- непрерывно дифференцируемые функции от x; - фундаментальная система решений соответствующего однородного уравнения; Н - порядок уравнения.
- фундаментальная система решений соответствующего однородного уравнения; Н - порядок уравнения.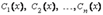 определяются из системы:
определяются из системы: 
 - правая часть заданного уравнения.
- правая часть заданного уравнения.



