
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання 1. Класичне означення ймовірностіСодержание книги
Поиск на нашем сайте
Завдання 1. Класичне означення ймовірності 1. Знайти ймовірність того, що серед 5 вибраних навмання цифр: а) немає цифри 0; б) немає цифри 1. 2. Знайти ймовірність того, що дні народження 12 осіб припадуть на різні місяці року. 3. У ліфті 6 пасажирів. Ліфт зупиняється на 10-ти поверхах. Яка ймовірність того, що всі пасажири вийдуть на різних поверхах? 4. Визначити, що ймовірніше: при підкиданні чотирьох гральних кісток отримати принаймні одну одиницю чи при 24 підкиданнях двох кісток отримати принаймні один раз дві одиниці. 5. В лотереї є 100 білетів, серед яких 10 виграшних. Обчислити ймовірність виграшу для того, хто купив 20 білетів. 6. В Андрія в кишені 5 ключів, з яких тільки один підходить до його дверей. Він послідовно без повернення витягує ключі до тих пір, поки не з’явиться потрібний ключ. Знайти ймовірність того, що потрібний ключ з’явиться при 3-му витягуванні. 7. Кинуто 6 гральних кісток. Знайти ймовірність того, що: а) на всіх кістках випаде різна кількість очок; б) сума всіх очок, що випали, дорівнює 7. 8. Знайти ймовірність того, що серед 7 вибраних навмання цифр: а) немає цифр 5 і 1; б) немає цифри 5 або немає цифри 1. 9. Гральну кісточку кидають 4 рази. Яка ймовірність того, що: а) хоча б 1 раз випаде 6, б) шестірка випаде точно один раз? 10. В урні 3 чорних і 7 білих кульок. З урни без повернення навмання витягнули дві кульки. Знайти ймовірність того, що: а) витягнули кульки одного кольору; б) витягнули кульки різного кольору. 11. Учаснику лотереї «Спортлото» з 36 видів спорту (позначених числами від 1 до 36) потрібно назвати 5. Повний виграш отримає той, хто правильно вкаже всі 5 назв. Виграші отримають і ті, хто вгадає не менше трьох назв. Обчислити ймовірність того, що учасник «Спортлото» відгадає 5, 4, 3 назви. Яка ймовірність отримати виграш у «Спортлото»? 12. 10 осіб, серед є особи А та В, шикуються в шеренгу в довільному порядку. Яка ймовірність того, що між особами А та В стане рівно 3 особи? 13. Написано 10 листів, але адреси на конвертах написані навмання. Яка ймовірність того, що принаймні один із адресатів отримає призначений для нього лист? 14. Для зменшення загальної кількості ігор 20 команд розбили на дві підгрупи по 10 команд в кожній. Яка ймовірність того, що дві найсильніші команди виявляться:
а) в різних підгрупах; б) в одній підгрупі? 15. Яка ймовірність того, що вісім тур, які навмання розміщені на шаховій дошці, не зможуть бити одна одну? 16. У три вагони поїзда заходять 9 пасажирів. Яка ймовірність того, що а) у перший вагон зайде 3 пасажири; б) в кожен вагон зайде по три пасажири; в) в один вагон зайде 4, в другий — 3, а в третій — 2 пасажири? 17. В групі є 25 студентів. Яка ймовірність того, що принаймні у двох з них збігаються дні народження? 18. Для зменшення загальної кількості ігор 20 команд розбили на дві підгрупи по 10 команд в кожній. Яка ймовірність того, що чотири найсильніші команди попадуть по дві в різні підгрупи? 19. 15 студентів і 15 студенток довільним чином займають місця в ряду з 30 місць. Яка ймовірність того, що: а) жодні дві студентки не сидітимуть поруч; б) всі студентки сидітимуть поруч? 20. На шахову дошку поставили навмання дві тури (білу і чорну). Що ймовірніше: битимуть чи не битимуть вони одна одну? 21. На іспиті може бути запропоновано 30 питань. Студент знає відповіді на 20. Екзаменатор задає студенту 10 питань. Для того, щоб скласти іспит, треба відповісти не менше, ніж на 5 питань. Яка ймовірність того, що студент складе іспит? 22. На поличці у випадковому порядку розташовано 40 книжок, серед яких — трьохтомник. Знайти ймовірність того, що ці томи будуть стояти в порядку зростання зліва направо, але не обов’язково поруч. 23. 10 осіб, серед є особи А та В, займають місця за круглим столом в довільному порядку. Яка ймовірність того, що особи А та В будуть сидіти поруч? 24. З колоди 36 карт довільним чином витягують дві карти. Яка ймовірність того, що: а) хоча б одна карта є тузом; б) обидві карти одної і тої ж масті? 25. З колоди 36 карт довільним чином витягується одна карта, після чого вона кладеться назад. Потім з колоди витягують дві карти. Знайти ймовірність того, що всі три карти однієї і тої ж масті.
Завдання 7 Знайти: · невідому константу · умовний розподіл компоненти
· перевірити, чи компоненти вектора · обчислити розподіл суми (для варіантів №1-6), різниці (для варіантів №7-12), добутку (для варіантів №13-18), частки (для варіантів №19-25) випадкових величин Розподіл ймовірностей випадкового вектора
Варіант 1 Варіант 2
Варіант 3 Варіант 4
Варіант 5 Варіант 6
Варіант 7 Варіант 8
Варіант 9 Варіант 10
Варіант 11 Варіант 12
Варіант 13 Варіант 14
Варіант 15 Варіант 16
Варіант 17 Варіант 18
Варіант 19 Варіант 20
Варіант 21 Варіант 22
Варіант 23 Варіант 24
Варіант 25
Завдання 8 Знайти: · розподіли компонент випадкового вектора · умовну щільність розподілу компоненти · математичне сподівання і коваріаційну матрицю вектора · умовні математичні сподівання · перевірити, чи компоненти вектора Щільність
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24)
Завдання 1. Класичне означення ймовірності 1. Знайти ймовірність того, що серед 5 вибраних навмання цифр: а) немає цифри 0; б) немає цифри 1. 2. Знайти ймовірність того, що дні народження 12 осіб припадуть на різні місяці року. 3. У ліфті 6 пасажирів. Ліфт зупиняється на 10-ти поверхах. Яка ймовірність того, що всі пасажири вийдуть на різних поверхах?
4. Визначити, що ймовірніше: при підкиданні чотирьох гральних кісток отримати принаймні одну одиницю чи при 24 підкиданнях двох кісток отримати принаймні один раз дві одиниці. 5. В лотереї є 100 білетів, серед яких 10 виграшних. Обчислити ймовірність виграшу для того, хто купив 20 білетів. 6. В Андрія в кишені 5 ключів, з яких тільки один підходить до його дверей. Він послідовно без повернення витягує ключі до тих пір, поки не з’явиться потрібний ключ. Знайти ймовірність того, що потрібний ключ з’явиться при 3-му витягуванні. 7. Кинуто 6 гральних кісток. Знайти ймовірність того, що: а) на всіх кістках випаде різна кількість очок; б) сума всіх очок, що випали, дорівнює 7. 8. Знайти ймовірність того, що серед 7 вибраних навмання цифр: а) немає цифр 5 і 1; б) немає цифри 5 або немає цифри 1. 9. Гральну кісточку кидають 4 рази. Яка ймовірність того, що: а) хоча б 1 раз випаде 6, б) шестірка випаде точно один раз? 10. В урні 3 чорних і 7 білих кульок. З урни без повернення навмання витягнули дві кульки. Знайти ймовірність того, що: а) витягнули кульки одного кольору; б) витягнули кульки різного кольору. 11. Учаснику лотереї «Спортлото» з 36 видів спорту (позначених числами від 1 до 36) потрібно назвати 5. Повний виграш отримає той, хто правильно вкаже всі 5 назв. Виграші отримають і ті, хто вгадає не менше трьох назв. Обчислити ймовірність того, що учасник «Спортлото» відгадає 5, 4, 3 назви. Яка ймовірність отримати виграш у «Спортлото»? 12. 10 осіб, серед є особи А та В, шикуються в шеренгу в довільному порядку. Яка ймовірність того, що між особами А та В стане рівно 3 особи? 13. Написано 10 листів, але адреси на конвертах написані навмання. Яка ймовірність того, що принаймні один із адресатів отримає призначений для нього лист? 14. Для зменшення загальної кількості ігор 20 команд розбили на дві підгрупи по 10 команд в кожній. Яка ймовірність того, що дві найсильніші команди виявляться: а) в різних підгрупах; б) в одній підгрупі? 15. Яка ймовірність того, що вісім тур, які навмання розміщені на шаховій дошці, не зможуть бити одна одну? 16. У три вагони поїзда заходять 9 пасажирів. Яка ймовірність того, що а) у перший вагон зайде 3 пасажири; б) в кожен вагон зайде по три пасажири; в) в один вагон зайде 4, в другий — 3, а в третій — 2 пасажири? 17. В групі є 25 студентів. Яка ймовірність того, що принаймні у двох з них збігаються дні народження? 18. Для зменшення загальної кількості ігор 20 команд розбили на дві підгрупи по 10 команд в кожній. Яка ймовірність того, що чотири найсильніші команди попадуть по дві в різні підгрупи?
19. 15 студентів і 15 студенток довільним чином займають місця в ряду з 30 місць. Яка ймовірність того, що: а) жодні дві студентки не сидітимуть поруч; б) всі студентки сидітимуть поруч? 20. На шахову дошку поставили навмання дві тури (білу і чорну). Що ймовірніше: битимуть чи не битимуть вони одна одну? 21. На іспиті може бути запропоновано 30 питань. Студент знає відповіді на 20. Екзаменатор задає студенту 10 питань. Для того, щоб скласти іспит, треба відповісти не менше, ніж на 5 питань. Яка ймовірність того, що студент складе іспит? 22. На поличці у випадковому порядку розташовано 40 книжок, серед яких — трьохтомник. Знайти ймовірність того, що ці томи будуть стояти в порядку зростання зліва направо, але не обов’язково поруч. 23. 10 осіб, серед є особи А та В, займають місця за круглим столом в довільному порядку. Яка ймовірність того, що особи А та В будуть сидіти поруч? 24. З колоди 36 карт довільним чином витягують дві карти. Яка ймовірність того, що: а) хоча б одна карта є тузом; б) обидві карти одної і тої ж масті? 25. З колоди 36 карт довільним чином витягується одна карта, після чого вона кладеться назад. Потім з колоди витягують дві карти. Знайти ймовірність того, що всі три карти однієї і тої ж масті.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.96 (0.011 с.) |

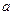 , розподіли компонент, математичне сподівання і коваріаційну матрицю випадкового вектора
, розподіли компонент, математичне сподівання і коваріаційну матрицю випадкового вектора  ;
; за умови, що
за умови, що  , умовний розподіл компоненти
, умовний розподіл компоненти  за умови, що
за умови, що  , умовне математичне сподівання компоненти
, умовне математичне сподівання компоненти  , умовне математичне сподівання компоненти
, умовне математичне сподівання компоненти  , якщо
, якщо  ;
;
 , умовну щільність розподілу компоненти
, умовну щільність розподілу компоненти  , тобто
, тобто 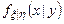 і
і  ;
; та
та  ;
; розподілу вектора
розподілу вектора  має такий вигляд:
має такий вигляд:





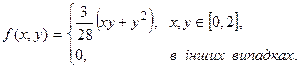




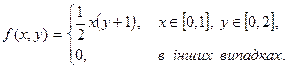

 R.
R.


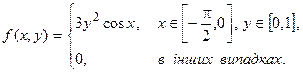

 R.
R.







