Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перехід від одного опорного рішення до іншого.Содержание книги
Поиск на нашем сайте
У транспортній задачі перехід від одного опорного рішення до іншого здійснюється за допомогою циклу. Для деякої вільної клітинки таблиці будується цикл, що містить частину клітинок, зайнятих опорним рішенням. По цьому циклу перерозподіляються об'єми перевезень. Перевезення завантажується у вибрану вільну клітинку і звільняється одна із зайнятих кліток, виходить нове опорне рішення. Теорема 6. (про існування і єдиність циклу). Якщо таблиця транспортної задачі містить опорне рішення, то для будь-якої вільної клітинки таблиці існує єдиний цикл, що містить цю клітинку і частину клітинок, зайнятих опорним рішенням. Доказ. Опорне рішення займає N=m+n-1 клітинок таблиці, яким відповідають лінійно незалежні вектори-умови. Якщо ж до зайнятих клітинок приєднати одну вільну, то відповідні їм m+n векторів лінійно залежні, і по тій же теоремі існує цикл, що містить цю клітинку. Припустимо, що таких циклів два (i1,j1 ), ( i1,j2 ), ( i2,j2 ), …, ( ik,j1) і (i1,j1 ), ( i2,j1 ), …, ( i1,ji). Тоді, об'єднавши клітинки обох циклів без вільної клітинки (i1,j1 ), одержимо послідовність клітинок ( i1,j2 ), …, ( ik,j1 ), (i2,j1), …, (i1,ji), які утворюють цикл. Це суперечить лінійній незалежності векторів-умов, створюючих базис опорного рішення. Отже, такий цикл єдиний. Зазначений цикл. Цикл називається зазначеним, якщо його кутові клітинки пронумеровані по порядку і непарним клітинкам приписаний знак «+», а парним – знак «-» (рис 2.) 1 2
- 5 + + - 3 4 рис 2.
Зрушенням по циклу на величину Теорема 7. Якщо таблиця транспортної задачі містить опорне рішення, то при зрушенні по будь-якому циклу, що містить одну вільну клітинку, на величину Доказ. У таблиці транспортної задачі, що містить опорне рішення, виберемо вільну клітинку і відзначимо її знаком «+». По теореме6. для цієї клітинки існує єдиний цикл, який містить частину клітинок, зайнятих опорним рішенням. Пронумеруємо клітинки циклу, починаючи з клітинки, відміченої знаком «+». Знайдемо У кожному рядку і в кожному стовпці таблиці, що входять в цикл, дві і лише дві клітинки, одна з яких відмічена знаком «+», а інша - знаком «-». Тому в одній клітинці об'єм перевезення збільшується на
Якщо залишити вільною одну з клітинок з нульовим об'ємом перевезення, відповідних Розподільний метод. Один з найпростіших методів рішення транспортної задачі – розподільний метод. Хай для транспортної задачі знайдене початкове опорне рішення Визначимо, як зміниться цільова функція при переході до нового опорного рішення. При зрушенні на одиницю вантажу по циклу, відповідному клітинці (l, до), приріст цільової функції У клітинках, відмічених знаком «+», величини вантажу додаються, що приводить до збільшення значення цільової функції Z(( Якщо різниця сум для вільної клітинки (l, до) менше нуля, тобто
Для вирішення транспортної задачі розподільним методом необхідно знайти початкове опорне рішення. Потім для чергової опорної клітинки (l, до) побудувати цикл і обчислити оцінку Для кожного нового опорного вирішення обчислення оцінок починається з першої вільної клітинки таблиці. Очевидність вільних клітинок, що перевіряються, доцільно встановлювати у порядку зростання вартості перевезень
Метод потенціалів. Широко поширеним методом рішення транспортних задач є метод потенціалів. Цей метод дозволяє спростити найбільш трудомістку частину обчислень – знаходження оцінок вільних клітинок. Теорема 8. (ознака оптимальності опорного рішення). Якщо допустиме рішення Х=((
Доказ. Використовуємо другу теорему подвійності. Запишемо математичну модель транспортної задачі
F(U, V)== Кожне обмеження подвійної задачі містить тільки дві змінні, оскільки вектор-умова Група рівності (12) Дана система рівнянь має m+n невідомих Група нерівностей (13) Числа
Оцінки для вільних клітинок транспортної таблиці використовуються для поліпшення опорного рішення. З цією метою знаходять клітинку (до, l) таблиці, відповідну max{{
Приклад Знайти оптимальний розв’язок транспортної задачі: А = (100; 200; 10; 50) B = (150; 50; 120; 40)
7 6 5 4 C = 4 3 4 7 6 7 6 6
Рішення:
å ai = 360; å bi = 360 å ai = å bi = 360 - задача закритого типу. Побудуємо опорний план методом мінімальної вартості:
V1 V2 V3 V4
Заповнення клітинок повинно бути m + n – 1
Z1 = 150 · 1 + 50 · 4 + 60 · 4 + 50 · 3 + 10 · 4 + 40 · 6 = 1020
Перевіримо план на oптимальність розподільним методом: C11 = 3 - 1 + 3 – 4 = 1 C12 = 2 – 4 + 3 – 1 = 0 C13 = 8 – 6 + 6 – 4 + 3 – 1 = 6 C21 = 7 – 4 + 6 – 6 = 3 C22 = 6 – 4 + 6 – 6 + 4 – 3 = 3 C23 = 5 – 4 + 6 – 6 + 4 – 4 = 1 C42 = 7 – 3 + 4 – 6 = 2 C43 = 6 – 4 + 4 – 6 = 0 Так як всі Cij ³ 0, то план оптимальний.
Перевіримо план на оптимальність методом потенціалів: u1 + v2 = 1 u1 = 0 v1 = 1 u2 + v4 = 4 u2 = 3 v2 = 1 u3 + v1 = 4 u3 = 3 v3 = 1 u3 + v2 = 3 u4 = 5 v4 = 1 u3 + v3 = 4 u4 + v1 = 6 u4 + v4 = 6
d11 = 3 – (0 + 1) = 2 d23 = 5 – (3 + 1) = 1 d13 = 2 – (0 + 1) = 1 d34 = 7 – (3 + 1) = 3 d14 = 8 – (0 + 1) = 7 d42 = 7 – (5 + 1) = 1 d21 = 7 – (3 + 1) = 3 d43 = 6 – (5 + 1) = 0 d22 = 6 – (3 + 1) = 2
Так як всі d ij ³ 0, то план оптимальний Z opt = 1020
Завдання для самостійного виконання Задача 1.
Деяке об’єднання складається з двох підприємств, які виготовляють столи та трьох меблевих магазинів. Виробництво столів першим підприємством описане в задачі 1., друге постачає столів у кількості 100 одиниць. Вартості перевезення одиниці продукції від підприємства до магазинів наведено в ум. од.:
Перший магазин реалізовує 10 одиниць продукції, другий – 25 і третій – 200. Знайти оптимальний план перевезень продукції, що дає можливість мінімізувати сумарну вартість перевезень. Врахувати умову, що з першого підприємства вся продукція має бути вивезена повністю. Задачі За наведеними в таблиці витратами на перевезення вантажу від пунктів постачання А1, А2, А3 до пунктів споживання В1, В2, В3, В4, а також обсягами запасів продукції в пунктах постачання та її попиту в пунктах споживання знайти оптимальний план транспортної задачі.
1. 2.
3.
4.
5.
6.
7.
8.
9.
10.
Варіант 01Варіант 03
А = (50, 40, 10, 100) А = (100, 180, 120, 130) В = (120, 10, 40, 30) В = (200, 110, 130, 140)
3 1 2 8 1 2 6 7 С = 7 6 5 4 С= 6 7 1 2 4 3 4 7 3 4 5 1 6 7 6 6 1 4 2 1 Варіант 02Варіант 04
А = (10, 100, 80, 70) А = (120, 80, 90, 10) В = (40, 60, 50, 200) В = (20, 40, 180, 50)
1 5 4 3 1 5 6 7 С = 6 7 2 1 С= 4 3 2 1 5 4 5 5 1 1 1 1 2 3 1 7 2 1 4 6 Варіант 05Варіант 09
А = (120, 80, 120, 200) А = (100, 20, 80, 10) В = (200, 100, 150, 50) В = (90, 50, 40, 70)
1 4 3 2 4 3 2 1 С = 5 6 7 1 С= 5 6 7 8 9 1 1 10 3 5 2 7 2 3 5 8 5 1 4 2
Варіант 06Варіант 10
А = (50, 40, 90) А = (100, 80, 30, 70) В = (30, 70, 80) В = (90, 50, 40, 70)
1 5 4 1 4 3 2 С = 2 6 7 С= 5 6 7 8 2 1 1 9 8 6 5 5 5 5 4 Варіант 07Варіант 11
А = (100, 200, 300, 150) А = (60, 40, 80, 50) В = (120, 80, 400, 100) В = (70, 30, 60, 70)
С = 2 5 6 2 С= 4 3 2 1 8 7 1 1 2 3 3 2 1 1 5 4 6 2 2 3
Варіант 08Варіант 12
А = (100, 50, 50, 200) А = (20, 10, 40, 50) В = (80, 30, 20, 170) В = (30, 15, 25, 40)
5 6 7 8 1 2 4 6 С = 4 5 3 2 С= 5 4 3 1 1 1 1 1 2 1 1 2 6 7 6 5 1 2 5 3 Варіант 13Варіант 17
А = (100, 200, 10, 50) А = (40, 20, 50, 10) В = (150, 50, 120, 40) В = (3, 17, 35, 45)
3 1 2 8 1 3 4 3 С = 7 6 5 4 С= 2 5 4 2 4 3 4 7 6 1 1 1 6 7 6 6 1 2 3 4 Варіант 14Варіант 18
А = (40, 80, 50, 50) А = (70, 60, 80) В = (100, 95, 45, 35) В = (70, 40, 80, 30)
1 5 4 3 3 2 3 1 С = 2 6 7 8 С= 4 5 4 2 7 8 4 2 8 4 5 8 1 1 1 1
Варіант 15Варіант 19
А = (10, 210, 10, 80) А = (30, 40, 10, 20) В = (120, 80, 90, 50) В = (40, 30, 150, 10)
3 1 2 8 1 2 3 4 С = 7 6 5 4 С= 5 3 1 6 4 3 4 7 7 4 2 5 6 7 6 6 6 3 8 1
Варіант 16Варіант 20
А = (60, 40, 30, 50) А = (100, 180, 120, 130) В = (70, 30, 40, 50) В = (200, 110, 130, 140)
3 4 2 1 1 2 6 7 С = 5 2 3 4 С= 6 7 1 2 1 8 7 2 3 4 5 1 2 3 6 5 1 4 2 1
Питання для самоконтролю Класичне формулювання транспортної задачі. Сформулюйте транспортну задачу за критеріями: Найменшої вартості перевезень Найменшого терміну перевезень За яких умов транспортна задача називається збалансованою? За яких умов транспортна задача називається незбалансованою? Як незбалансовану транспортну задачу привести до збалансованої? Що таке опорний план перевезення? Методи його обчислення? Скільки компонент повинно бути в опорному плані? За яких умов транспортна задача називається виродженною? Що таке цикл у розподільчій матриці ТЗ? Метод потенціалів розв’язання транспортної задачі? Розподільний метод розв’язання ТЗ? За яких умов наявний план перевезення буде оптимальним?
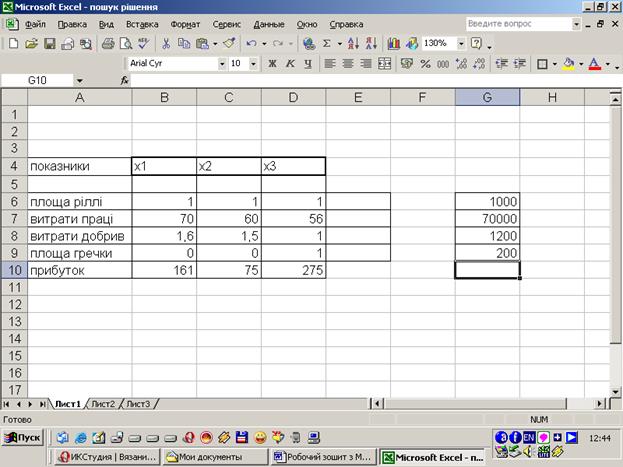
Тема 6. Пошук рішення При аналізі табличних даних в Excel можна для заданого значення результату і певних умов (обмежень) визначити величини впливових змінних. Це здійснюється за допомогою програми пошуку рішень. Вирішення оптимізацій них задач За допомогою настройки Поиск решения потрібно визначити структуру посівів озимої пшениці, проса і гречки, щоб прибуток від реалізації продукції був максимальним при таких умовах: загальна площа посіву не перевищує –1000га; запаси мінеральних добрив – 1200 ц.д.р.; трудові ресурси 70000 люд.-год.; площа гречки не більше 200 га. Нормативи затрат праці, добрив і розмір прибутку в розрахунку на 1га. Посівів наведені в таблиці. 6.1 Табл. 6.1
Для рішення задачі слід скласти її математичну модель: Знайти МАХ цільової функції: С=161х При таких обмеженнях: х 70х 1,6х х Пошук рішення здійснюється у такій послідовності дій: розташувати вихідні данні так, як показано на таблиці рис 6.1;
Рис. 6.1. Вихідні дані установити курсор у чарунку Е6; використовуючи майстра функцій, обчислити функцію СУММПРОЗИВ, де у поле Массив 1 вивести діапазон чарунок В5:D5 і натиснути клавішу [f4] щоб зробити цю адресу абсолютною, у поле Массив 2 – відповідно B6:D6 і натиснути кнопку ОК (згідно обмеженню першому); продублювати цю формулу у чарунку Е6:Е10 (згідно обмеження цільової функції) (рис. 6.2)
Рис. 6.2. Розрахунки установити курсор у чарунку Е10 – цільова функція; вибрати команду Сервис – Поиск решения; у вікні Поиск решения заповнити так поля, як указано (обмеження додавати за допомогою кнопки Добавить (рис.6. 3))
Рис. 6.3. Додавання обмежень
натиснути кнопку Параметры і встановити параметри, як вказано на рис 6.4, і натиснути кнопку ОК;
Рис. 6.4. Встановлення пареметрів
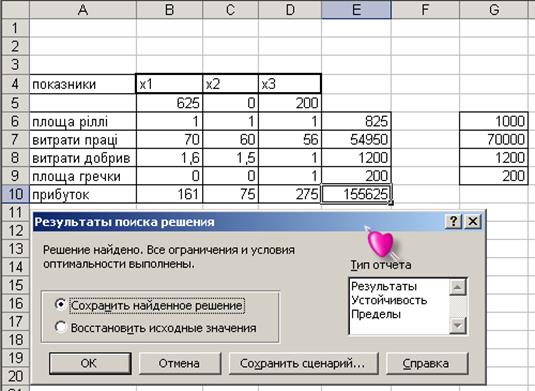
у вікні Поиск решения натиснути кнопку Выполнить; якщо результати вас задовольняють, у вікні Результаты поиска решения (рис. 6.5) вибрати перемикач Сохранить найденое решение і натиснути кнопку ОК.
Рис. 6.5. Результати пошуку рішення
На рис. 6.5 бачимо результати розв’язання задачі. Площа озимої пшениці – 625 га, Гречки – 200 га, прибуток – 155625 грн, використано всі ресурси по добривах, але залишилися недовикористаними площа та трудові ресурси.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.18.190 (0.01 с.) |


 + -
+ - називається збільшення об'ємів перевезень у всіх непарних клітинках циклу, відмічених знаком «+», на
називається збільшення об'ємів перевезень у всіх непарних клітинках циклу, відмічених знаком «+», на  вийде опорне рішення.
вийде опорне рішення.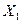 і обчислене значення цільової функції на цьому рішенні Z((
і обчислене значення цільової функції на цьому рішенні Z((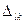 рівно різниці двох сум:
рівно різниці двох сум: 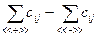 , де
, де  - сума вартостей перевезень одиниць вантажу в непарних клітинках циклу, відмічених знаком «+»,
- сума вартостей перевезень одиниць вантажу в непарних клітинках циклу, відмічених знаком «+»,  - сума вартостей перевезень одиниць вантажу в парних клітинках циклу, відмічених знаком «-».
- сума вартостей перевезень одиниць вантажу в парних клітинках циклу, відмічених знаком «-». ), а в клітинках, відмічених знаком «-», величини вантажу зменшуються, що приводить до зменшення значення цільової функції.
), а в клітинках, відмічених знаком «-», величини вантажу зменшуються, що приводить до зменшення значення цільової функції.
 =0. (11)
=0. (11) , оскільки розв'язується задача на знаходження мінімуму.
, оскільки розв'язується задача на знаходження мінімуму. ), i=1,2,,…,m, j=1,2,…,n транспортної задачі є оптимальним, то існує потенціали (числа) постачальників
), i=1,2,,…,m, j=1,2,…,n транспортної задачі є оптимальним, то існує потенціали (числа) постачальників  , i=1,2,,…,m і споживачів
, i=1,2,,…,m і споживачів  , j=1,2,…,n, задовольняючі наступним умовам:
, j=1,2,…,n, задовольняючі наступним умовам: при
при 

 ,
,
 , i=1,2,,…,m,
, i=1,2,,…,m,  , j=1,2,…,n,
, j=1,2,…,n,  0, i=1,2,,…,m, j=1,2,…,n.
0, i=1,2,,…,m, j=1,2,…,n. ,
,  системи обмежень початкової задачі має тільки дві відмінні від нуля (рівні одиниці) координати,i-ю і (m+j) -у. Умов позитивності подвійна задача не має, оскільки всі обмеження в початковій задачі – рівність. По другій теоремі подвійності, якщо при підстановці в систему обмежень подвійної задачі деяке обмеження виконується як строга нерівність
системи обмежень початкової задачі має тільки дві відмінні від нуля (рівні одиниці) координати,i-ю і (m+j) -у. Умов позитивності подвійна задача не має, оскільки всі обмеження в початковій задачі – рівність. По другій теоремі подвійності, якщо при підстановці в систему обмежень подвійної задачі деяке обмеження виконується як строга нерівність  >0.
>0.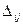 }==
}== 
 3 1 2 8
3 1 2 8
 Ai
Bi
Ai
Bi








 1 2 3 7 1 2 4 6
1 2 3 7 1 2 4 6


 +75х
+75х  +275х
+275х  , де змінні х
, де змінні х