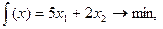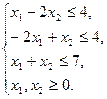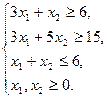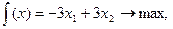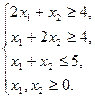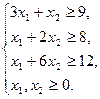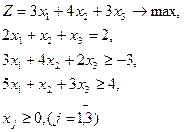Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Двоїста задача лінійного програмуванняСодержание книги
Поиск на нашем сайте
Правила побудови двоїстої задачі лінійного програмування: Кожній задачі лінійного програмування можна поставити у відповідність іншу, пов’язану певним чином з початковою задачею. Такі задачі називають двоїстими, або спряженими. Спільний розгляд двоїстих пар задач дуже важливий в економічному аналізі оптимального плану. Відповідність між вихідною та двоїстою задачами полягає в побудові на основі першої задачі двоїстої до неї /як вихідна може розглядатися будь-яка зі спряженої пари задач/. Двоїсті задачі бувають симетричні і несиметричні. Симетричні задачі Початкова задача Двоїста задача
Якщо обмеження вихідної задачі записано у вигляді рівнянь, то побудована до неї двоїста задача називається несиметричною. Водночас змінні
Розглянемо правила побудови двоїстої задачі. 1. Кожному і - му обмеженню вихідної задачі відповідає змінна 2. Якщо одна з пари двоїстих задач сформульована на максимум цільової функції, то друга - на мінімум і навпаки. 3. Обмеження-нерівності слід записувати зі знаком « 4. Коефіцієнти цільової функції однієї із задач є вільними членами системи обмежень другої задачі. 5. Матриці, складені з коефіцієнтів обмежень вихідної і двоїстої задач, є взаємно транспонованими. Оптимальні розв’язки двоїстих задач тісно пов’язані між собою. Основою для їх аналізу є наведені далі теореми двоїстості. Теорема 1.1. /Перша теорема двоїстості/. Якщо одна зі спряжених задач має оптимальний план, то його має й друга задача, причому значення цільових функцій збігаються, тобто Якщо цільова функція однієї із задач не обмежена на множині змінних, то друга задача розв’язку не має. Оптимальний розв’язок двоїстої задачі знаходять за даними останьої симплексної таблиці вихідної задачі за формулою
Зауважимо, що для оптимального плану вихідної задачі матриця Зауважимо, що Теорема 1.2. /Друга теорема двоїстості/. Якщо при підстановці компонентів оптимального плану в і - те або j - те обмеження вихідної /двоїстої/ задачі це обмеження виконується як рівняння, то відповідна змінна спряженої задачі буде строго більша від нуля, а коли воно виконується як строга нерівність, то відповідна змінна спряженої задачі дорівнює нулю. Наведемо формальний запис цієї теореми для задач /1.10/ - /1.12/ і /1.10а/ - /1.12а/. Нехай дано оптимальний план вихідної задачі у вигляді Тоді маємо: якщо якщо У разі, коли дано оптимальний план двоїстої задачі якщо якщо Теорема 1.3. /Третя теорема двоїстості./ Двоїсті оцінки показують приріст цільової функції, який зумовлюється малою зміною вільного члена відповідного обмеження:
або Приклад 1.1. Розв’язати двоїсту задачу, використовуючи розв’язок вихідної
Записуємо двоїсту задачу
Здобута пара задач несиметрична, оскільки обмеження вихідної задачі записані в канонічній формі. Отже, двоїсті змінні У - довільні /можуть бути як додатними, так і від’ємними або такими, що дорівнюють нулю/.
Задачі для самостійного розв’язання Розв’язати задачу лінійного програмування, записати і розв’язати двоїсту до неї задачу.
Питання для самоконтролю
Економічний сенс задачі, спряженої до задачі планування обсягів виробництва. За яких умов спряжені задачі називаються симетричними? Якими правилами необхідно користуватися, формулюючи спряжену симетричну задачу? Як пов’язані оптимальні розв’язки спряжених задач? Як пов’язані змінні вихідної та спряженої задач? Як побудувати оптимальний план спряженої задачі за наявності такого плану вихідної задачі? Що стверджують основні теореми спряженості?
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

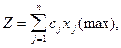 /1.10/
/1.10/  /1.10а/
/1.10а/ /1.11/
/1.11/  /1.11а/
/1.11а/ /1.12/
/1.12/ 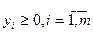 /1.12а/
/1.12а/ можуть бути як додатні, так і від’ємні, тобто не виконується умова
можуть бути як додатні, так і від’ємні, тобто не виконується умова  , а саме:
, а саме:

 вихідної задачі.
вихідної задачі. » - при мінімізації цільової функції.
» - при мінімізації цільової функції.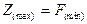 .
.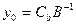 , де
, де  - матриця-рядок двоїстих змінних
- матриця-рядок двоїстих змінних  ;
; - матриця-рядок, складена з коефіцієнтів цільової функції для базисних змінних останньої симплексної таблиці вихідної задачі;
- матриця-рядок, складена з коефіцієнтів цільової функції для базисних змінних останньої симплексної таблиці вихідної задачі; - матриця обернена до матриці В, складеної з компонентів базисних векторів останньої симплексної таблиці вихідної задачі.
- матриця обернена до матриці В, складеної з компонентів базисних векторів останньої симплексної таблиці вихідної задачі. вихідної задачі. Змінні оптимального плану
вихідної задачі. Змінні оптимального плану  двоїстої задачі розміщуються під відповідними одиничними векторами
двоїстої задачі розміщуються під відповідними одиничними векторами  в рядку (m+1), причому їх значення дорівнюють
в рядку (m+1), причому їх значення дорівнюють  .
.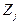 визначається додаванням до відповідної оцінки
визначається додаванням до відповідної оцінки  коефіцієнтів
коефіцієнтів  . Вважаємо, що одинична матриця в початковій задачі утворена векторами
. Вважаємо, що одинична матриця в початковій задачі утворена векторами 
 .
.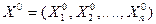 .
.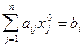 , то
, то  ;
; , то
, то  .
. дістаємо:
дістаємо: , то
, то  ;
; , то
, то  .
.
 .
.