
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кількість інформації та ентропіяСодержание книги
Поиск на нашем сайте
4.1.1 Моделі Хартлі (Шеннона)
Джерело інформації, яке може в кожний момент часу знаходитися в одному з можливих станів, називається дискретним джерелом інформації. Називатимемо кінцеву множину всіх можливих станів {u1, u2., uN} абеткою джерела (N – розмір абетки або число можливих станів). У загальному випадку різні стани ui вибираються джерелом з різною вірогідністю pi, і його можна охарактеризувати сукупністю абетки і безлічі вірогідності станів – ансамблем UN = {u1, p1, u2, p2., uN, pN}. Зрозуміло, сума вірогідності всіх станів повинна дорівнювати 1. Введемо міру невизначеності стану джерела H(U), що задовольняє таким умовам: · монотонність: міра повинна монотонно зростати із зростанням кількості можливих станів; · адитивність: міра, обчислена для складного джерела, що складається з двох незалежних джерел (з розмірами абеток N і M, тоді розмір абетки складного джерела – NM), повинна дорівнювати сумі мір цих двох джерел. Згідно з умовою адитивності міра повинна задовольняти співвідношенню:
Крім того, існує гранична умова: міра невизначеності для джерела з розміром алфавіту 1 повинна дорівнювати 0. Можна показати, що цим умовам задовольняє логарифмічна функція (з довільною основою). Для джерела з абеткою розміру N і рівноімовірними станами (pi = 1/N для будь-якого i) логарифмічна міра була запропонована Р. Хартлі у 1928 р. і має вигляд:
Припущення про рівні імовірності станів джерела інформації називається моделлю Хартлі. Якщо основу логарифма вибрати рівною двом, відповідна одиниця невизначеності відповідатиме невизначеності вибору з двох рівноімовірних подій і називатиметься двійковою одиницеюабо бітом (від англ. bit, скороченого binary digit, – двійкова цифра). Моделі Хартлі бракує врахування вірогідності станів. Якщо, наприклад, джерело має два можливі стани з вірогідністю 0.999 і 0.001, зрозуміло, що міра невизначеності такого джерела повинна бути менша 1 біта: є велика упевненість у виборі першого стану. Якщо вірогідність станів відрізняється трохи (наприклад, 0.51 і 0.49), то й міра невизначеності повинна змінитися трохи порівняно з рівноімовірним випадком. Таким чином, міра невизначеності повинна залежати від вірогідності станів джерела, від всього ансамблю. Така модель джерела інформації називається моделлю Шеннона(1948 р.). Міра невизначеності вибору дискретним джерелом стану з ансамблю UN називається ентропією дискретного джерела інформації або ентропією кінцевого ансамблю.
де C – довільне позитивне число. За умови рівної вірогідності станів джерела міра Шеннона зводиться до міри Хартлі. Доведено, що приведена функція – єдина і така, що задовольняє всім переліченим умовам. Термін “ентропія” запозичений з термодинаміки і використаний для міри невизначеності через те, що обидві ентропії – термодинамічна й інформаційна – характеризують ступінь різноманітності станів даної системи і описуються аналогічними функціями.
4.1.2 Властивості ентропії:
· Ентропія обмежена зверху значенням 1. · Ентропія рівна 0, тільки якщо один із станів має вірогідність, рівну 1 (повністю певне джерело). · Ентропія максимальна, коли всі стани джерела рівноімовірні. При цьому · Ентропія джерела з двома станами змінюється від 0 до 1, досягаючи максимуму при рівності їх вірогідності. · Ентропія об'єднання декількох незалежних джерел інформації дорівнює сумі ентропій початкових джерел. · Ентропія характеризує середню невизначеність вибору одного стану з ансамблю, не враховуючи змістовну сторону (семантику) станів. Одиниці кількості інформації. Біт – дрібна одиниця вимірювання кількості інформації. Крупніша одиниця – байт, що складається з восьми бітів. В мережах застосовуються і більш крупніші одиниці від кілобайтів (Кбайт) – 1024 байт = 210 байт до петабайтів (Пбайт) – 1024 Тбайт = 250 байт. За одиницю кількості інформації можна було б вибрати кількість інформації, що міститься, наприклад, у виборі одного з десяти рівновірогідних повідомлень. Така одиниця має назву діт або десятковою одиницею.
|
|||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.78.146 (0.007 с.) |

 . (4.1)
. (4.1) . (4.2)
. (4.2)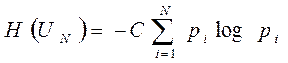 , (4.3)
, (4.3)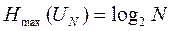 .
.


