Сдвиг, масштабирование и вращение с помощью мыши

Нажмите и удерживайте правую кнопку мыши для сдвига, масштабирования или вращения видов.

· Для сдвига в окне с параллельным проецированием просто перемещайте мышь.

· Для сдвига в окне с перспективным проецированием также перемещайте, удерживая дополнительно клавишу SHIFT.

· Для масштабирования (увеличения или уменьшения), удерживая клавишу CTRL, перемещайте мышь вверх или вниз соответственно.

· Для вращения вида с перспективным проецированием перемещайте мышь.

Это один из многих способов изменения параметров видов. Также аналогичные операции можно выполнить при помощи меню или панели инструментов (верхней), для дополнительной информации ищите Масштабирование (Zoom) в справочной системе Rhino.

Другие манипуляции

Протяженное масштабирование (Zoom Extents) установит такой масштаб вида, при котором все объекты сцены будут видны в одном окне проекции.

Применительно к одному виду:

· View \ Zoom \ ExtentsКоманда: ze

Применительно ко всем видам:

· View \ Zoom \ Extents AllКоманда: zea

Если вы хотите узнать больше о командах, оперирующих с видами, ищите раздел Виды (Vies) в справочной системе Rhino.

 

Ввод координат

Всякий раз, когда вы создаете кривую, устанавливаете точку, или создаете тело (из базового набора), Rhino запрашивает координаты некоторых точек. Когда требуется ввести координаты в командной строке, появляется подсказка Выбери точку (Choose a point) и курсор мыши превращается в перекрестие . Таким образом, можно указать координаты двумя способами: при помощи мыши указать точку в окне проекции или ввести их с клавиатуры, в командной строке.

О системах координат

Мировая (глобальная) система координат

Мировая система координат (МСК/WCS)–основная и абсолютная система координат, в Rhino она не претерпевает никаких изменений. В ее основе лежат x, y и z оси. Координаты в мировой системе координат отображаются в левом нижнем углу главного окна программы.

Конструкционные планы

В дополнение к мировой системе координат каждое проекционное окно базируется на конструкционном плане (К-Плане). К-План может быть ориентирован произвольно, т.к. он не зависим от мировой координатной системы.

Конструкционный план определяет координатную систему каждого окна проекций. Конструкционные планы могут быть, и по умолчанию так и есть, различными для разных окон проекций.

Всякий раз, когда вы мышью указываете точку, эта точка будет находиться на К-Плане, за исключением случая, когда используется режим Osnap.

Применения конструкционных планов

Иногда необходимо вводить координаты точек, которые нелегко представить в мировой системе координат. Например, как на рис. 17.

 

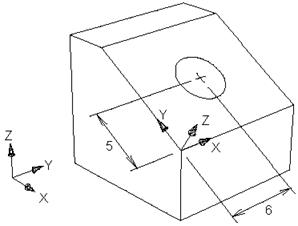
Рис. 17. Применение конструкционного плана

Нелегко разместить окружность на поверхности детали, используя мировую систему координат, но задача существенно упроститься, если вы определите новый К-План. Дополнительную информацию вы можете найти в справочной системе Rhino, в разделе К-План (CPlane).

На рисунке 18 демонстрируется К-План, расположенный в плоскости интересующей нас поверхности блока, начало его системы координат находится в нижнем левом углу поверхности.

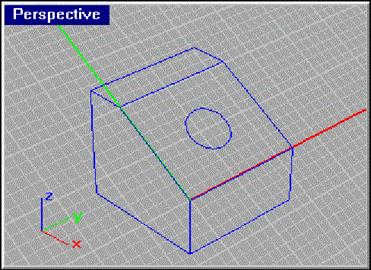
Рис. 18. К-План

 

Обратите внимание, что расположение осей мировой системы координат отличается от осей К-Плана.

Ввод точных координат

Когда Rhino предлагает вам указать точку, вы можете ввести точные координаты в многих координатных системах. Наиболее просто сделать это в 2D Декартовых координатах.

D Декартовы координаты

Когда Rhino предлагает вам указать точку, вы можете напечатать 2D Декартовы координаты, относительно координат К-Плана текущего окна. Имейте в виду, что точка, введенная в окне вида сверху, отличается от точки с теми же координатами окна вида справа, поскольку у этих видов разные К-Планы и, следовательно, разные координатные системы.

Что бы ввести 2D Декартовы координаты, нажмите на подсказку Укажите точку (Choose a point), введите координаты в формате x, y, где x и y-координаты желаемой точки.

D полярные координаты

Также можно ввести координаты и в полярной системе координат текущего К-Плана (рис. 19). Имейте в виду, что точка, введенная в окне вида сверху отличается от точки, с теми же координатами окна вида справа, поскольку у этих видов разные К-Планы и, следовательно, разные координатные системы.

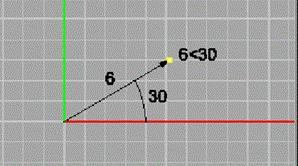
Рис. 19. Ввод координат в 2D полярных координат

 

Чтобы ввести 2D полярные координаты, нажмите на подсказку Укажите точку (Choose a point), введите координаты в формате d < a, где d –расстояние от точки отсчета; a –угол, отложенный от оси x.

Символ < используется, потому что похожий на него символ Ð в геометрии обозначает угол.

 

D относительные координаты

Rhino запоминает координаты последней введенной точки, и вы можете указать координаты новой точки относительно ранее введенной. Относительные координаты полезны при вводе групп точек с известнми относительными координатами.

Относительные координаты используют координатную систему К-Плана текущего вида.

Чтобы ввести 2D относительные Декартовы координаты, получив запрос Укажите точку (Choose a point), введите координаты, в формате rx, y, где r –указывает на Декартовы координаты относительно предыдущей точки (рис. 20). Если вы привыкли работать в AutoCAD и других аналогичных программах, то формат @x, y также работает.

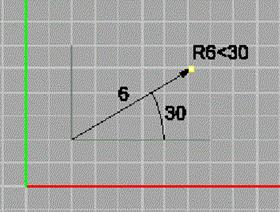
Рис. 20. 2D относительные Декартовы координаты

Чтобы ввести 2D относительные полярные координаты, получив запрос Укажите точку (Choose a point), введите координаты, в формате rd < a, где r –указывает на полярные координаты относительно предыдущей точки (рис. 21). Если вы привыкли работать в AutoCAD и других аналогичных программах, то формат @d < a также работает.

 

Рис. 21. 2D относительные полярные координаты

 

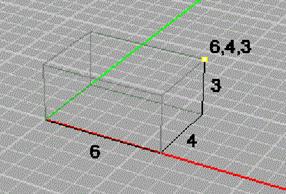
D Декартовы координаты

Метод ввода 2D Декартовых координат может быть расширен для ввода 3D координат. Когда Rhino предлагает вам указать точку вы можете ввести 3D координаты, относительно текущего К–Плана.

Чтобы ввести 3D Декартовы координаты, получив запрос Укажите точку (Choose a point), введите координаты в формате x, y, z, где x, y и z–координаты желаемой точки (рис. 22).

 

Рис. 22. 3D Декартовы координаты