
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класс моделей линейных объектов
Линейный объект в векторном формате пространственных данных определяется последовательной цепью отрезков
где ln – отрезки, составляющие полилинию L, n – номера узловых точек (узлов), координаты которых Xn, Yn задаются в виде последовательного списка. В свою очередь, текущие отрезки ln представляют собой множество точечных объектов
где Xn и Yn – множество координат точек, определяемых из выражения для прямой, проведенной через два соседних узла n и n + 1:
Из выражений (39) и (40) следует, что модель (функция) влияния линейного объекта fVL может быть определена как множество функций влияния точечных объектов fVP Основной задачей при определении моделей влияния линейных объектов является определение кратчайшего расстояния rij, которое зависит от взаимного расположения ломаной L и текущей точки Pi. Алгоритм поиска кратчайшего расстояния состоит в последовательном определении расстояний между каждым отрезком, составляющим полилинию L, и точкой прилегающей территории Pi и выбором из этих расстояний минимального ri min. Алгоритм вычисления ri min зависит от взаимного положения отрезка l и отрезков rin и rin +1, соединяющих i -ю точку территории с узловыми точками n и n +1. Рассмотрим типовые взаимные положения отрезка ln, заданного узлами P 1, P 2, и текущих точек P 3 – P 9 (рис. 24). Как видно, точки могут лежать на самом отрезке (P 3), на линии продолжения этого отрезка (P 4), на перпендикуляре к ln, проходящем через узлы (P 5, P 6), слева и справа от этих перпендикуляров (P 7, P 8) и на участках между перпендикулярами (P 9). Представим уравнение отрезка (41) в следующем виде:
где Тогда взаимоположение отрезков будет однозначно определяться их коэффициентами наклона k.
Рис. 24. Аморитм поиска кратчайшего расстояния rij от точки Рi до ломаной l
Для случаев, представленных на рис. 24, имеем:
где i = 3,4,...,7. Тангенсы углов между l, rin, rin +1 определяются выражением:
Алгоритм вычисления ri min будет следующим: 1. По выражениям (32), (33) вычисляются коэффициенты наклона отрезков и тангенсы углов между ними. 2. Если g 1· g 2= 0 (случай, когда kn = kn +1 = k l) и если (Xi - Xn)(Xi - Xn +1)£0, то текущая точка лежит на отрезке l (точка P 3) и r min = 0. иначе текущая точка лежит на линии продолжения отрезка l (точка P 4);
где 3. Если g 1· g 2 = ¥ (случай, когда 4. Если g 1· g 2 > 0, значит оба угла между l и r тупые (точка P 7) или острые (точка P 8), следовательно:
т.е. определяется расстояние до ближайшего узла отрезка ln. 5. Если g 1· g 2 < 0, значит один из углов – острый, а другой – тупой (точка P 9), тогда ri min равен длине перпендикуляра, опущенного из текущей точки на отрезок ln (расстояние Координата j -й точки пересечения отрезка ln и перпендикуляра, проходящего через текущую i -ю точку, для рассматриваемого случая определяется системой уравнений
Подставляя выражения для координат Xj, Yj в формулу для вычисления расстояния между двумя точками, окончательно получаем:
6.Переход к следующему отрезку, n ® n + 1, алгоритм вычисления начинается с первого пункта. Из получаемых значений ri min для отрезков ln и ln +1 выбирается меньшее и т.д., до полного перебора всех отрезков, составляющих полилинию. 7. В случае несимметричной модели влияния (Rij = fR (a ij)) определяется угол наклона отрезка ri min a ij = arctg kl – для точки P 4; a ij = arctg kin – для точки P 7; a ij = arctg k in +1 – для точки P 8; a ij + p/2 = arctg kl – для точек P 5, P 6, P 9; 8. По определенным значениям ri min, a ij и заданной аналитически или таблично функции fVT определяется величина влияния объекта в i- й точке Sij. Следующей по сложности является модель линейного объекта с переменным вдоль этого объекта коэффициентом веса (максимальным значением влияния) S j, т.е.
Sj = fS (lj), где lj – расстояние вдоль полилинии от начальной узловой точки до текущей j -й точки этой полилинии. В общем случае функция влияния fs может меняться в зависимости от расстояния l. Эта модель отражает, например, распространение загрязнения от некоторого источника вдоль реки с учетом воздействия на прилегающую территорию, изменение величины напряжения в ЛЭП и т.п. Модели, отражающие действие разнородных (противоречивых) факторов, как и в случае точечных объектов, строятся в виде комбинации простых моделей (рис. 25).
Сложная модель с симметричным Простая модель с асимметричным законом влияния законом влияния
Сложная модель с асимметричным законом влияния
Рис. 25. Класс моделей пространственного влияния линейных объектов (на примере функции влияния по нормальному закону распределения) Примером применения такой модели может служить задача, рассмотренная в § 1 гл. II, при учете противоречивых факторов влияния дороги на выбор участка для строительства. Рассмотренный класс моделей логично организуется в виде трехуровневой иерархии по принципу «от простого к сложному» (см. рис. 25). Такая структуризация моделей делает удобной процедуры формирования моделей, описывающих явления самой разнообразной природы, методами объектно-ориентированного проектирования, а также поиска нужных моделей из имеющихся библиотек.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.182.179 (0.008 с.) |
 , (39)
, (39) , (40)
, (40) . (41)
. (41) . (42)
. (42) , (43)
, (43)





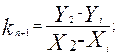


 ,
,

 ), текущая точка лежит на перпендикуляре, проходящем через узел (точки P 5, P 6), то определяются длины этих перпендикуляров
), текущая точка лежит на перпендикуляре, проходящем через узел (точки P 5, P 6), то определяются длины этих перпендикуляров  .
. или
или  ,
, ).
).

 .
.
 Простая модель с симметричным законом влияния
Простая модель с симметричным законом влияния








