
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класс моделей точечных объектовСодержание книги Поиск на нашем сайте
Базовый класс объектов, определяющих свойства территории, вполне естественно образуют точечные объекты. В пространственной БД множество таких объектов P задается множеством координат точек положения этих объектов:
где Pj – j -й точечный объект, положение которого определяется парой координат (Xi, Yj). Значение координат положения объекта может задаваться с любой точностью в диапазоне от нуля до максимальных значений координат X max, Y max того масштаба, в котором представлена цифровая карта рассматриваемой территории. В дальнейшем для единообразия индексы координат X и Y будем обозначать одной буквой j. Наиболее простой моделью влияния является симметричная, задаваемая какой-либо аналитической функцией. Эти модели можно разделить на две группы: с конечным радиусом влияния Rj (см. выражение (24) и с бесконечным. На рис. 22 представлены графики симметричных функций влияния с конечным радиусом (рис. 22, а и 22, б) и с бесконечным (рис. 22, в).
а б в Рис. 22. Примеры графиков функций влияния: а,б – графики симметричных функций влияния с конечным радиусом; в – графики симметричных функций влияния с бесконечным радиусом На первом графике (рис. 22, а) отображена линейная зависимость
где в соответствии с обозначениями, принятыми в выражении (24), rij – Радиус, или диапазон, влияния объекта определяется из условия Sij = 0. Например, для линейной ФПВО (выражение (32)
Алгоритм расчета величины влияния объекта (27) предельно прост: 1. определяется 2. если rij ³ Rj, то Sij =0; если rij < Rj, то вычисляется Sij. Задача решается путем перебора для всех i Î I, где I – множество узловых точек ЭУ wi (см. выражение (10). Аналогично для графика на рис. 22, б (параболическая зависимость)
Радиус (диапазон) влияния вычисляется из выражения
Данную группу объектов может определять бесчисленное множество функций fV, которым соответствуют различные физические или социально-экономические процессы и факторы. Например, функция (32) может отражать уменьшение положительного влияния склада с учетом времени перевозки продукции, а выражение (33) определяет то же самое, но с учетом времени и стоимости перевозки при ограничениях на уровне Sj. На рис. 22, в представлен график функции влияния, определяемый нормальным законом распределения:
где s j, m j – соответственно среднеквадратичное отклонение и величина математического ожидания. Выражение (34) достаточно часто применяется для построения моделей, т.к. нормальный закон распределения наиболее точно описывает пространственное влияние, обусловленное большим количеством слабо коррелированных факторов. Для формирования моделей влияния точечных объектов выражение (34) представим в следующем виде:
Теоретически радиус влияния равен бесконечности. Поэтому величина R определяется по допустимой величине
где n < 1 – допустимая часть от максимального значения Sij. Подставляя формулу (36) в выражение (35), получим:
или величина радиуса влияния будет определяться как Аналогично вычисляются значения Rj и для других видов функций fV. На практике задание моделей влияния наиболее удобно осуществлять следующими характеристиками: Sj, Rj, fV, задаваемыми аналитически или таблично. Это обусловлено тем, что величины Sj и Rj имеют наиболее наглядную и подходящую для экспертных оценок интерпретацию. Поэтому коэффициенты, входящие в выражения для f V (32), (33), (34), должны определяться через Rj. Соответственно для этих выражений получим
При табличной форме задания функции fV возникает проблема дискретности задания. Задание возможно в виде двумерного массива Очевидно, выходом является использование при расчете значений Sij процедуры интерполяции табличных значений. Наиболее эффективно интерполяция достигается с помощью сплайнов [32]. Следующим уровнем по сложности являются модели точечных объектов, отражающие несимметричное пространственное влияние. Типичные примеры такого влияния – это модели распространения выбросов из трубы ТЭЦ с учетом розы ветров, разлив воды из скважины с учетом рельефа местности и т.д. В этих моделях величина влияния Sij зависит не только от расстояния от текущей точки территории до объекта влияния, но и от направления:
где rij – расстояние между i -й точкой и j -м объектом, a ij – угол между, например, положительным направлением оси X и линией, соединяющей i -ю точку и j -й объект. Соответственно радиус влияния (или в этом случае более точно – диапазон) модели такого объекта будет зависеть от угла направления влияния
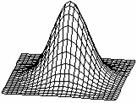
Следовательно, алгоритм расчета величины влияния в i -й точке усложняется: 1. определение 2. определение 3. расчет значения 4. если rji ³ Rij для фиксированного a ij, то Sij = 0; если rji £ Rij, то величина Sij вычисляется или берется из таблицы. Наиболее сложными являются модели, отражающие действие противоречивых (противоположных по свойствам) факторов влияния объектов, величина которых зависит от расстояния rij и угла действия a ij. Примером этому могут служить промышленные объекты. Их строительство вблизи от жилых кварталов нежелательно из-за возможного ухудшения экологической обстановки, удаленное размещение также нежелательно из-за увеличения затрат на транспортные расходы. Построение такого рода комбинированных моделей предлагается осуществлять путем сложения простых моделей, отражающих действий каждого из противоположных факторов или действий отдельных составляющих, имеющих различные функции влияния (рис. 23).
Простая модель с симметричным
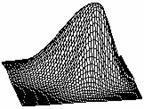
Комбинационная модель Простая модель с асимметричным
Комбинационная модель с асимметричным законом влияния Рис. 23. Класс моделей пространственного влияния точечных объектов Таким образом, результирующее влияние (действие) объекта на i -ю точку территории определяется выражением:
где Практически величина N редко превышает 2
Совокупность рассмотренных моделей представляет собой трехуровневую иерархию (см. рис. 23), в основу которой положен принцип «от простого к сложному». Представленная структура может служить основой при составлении библиотеки МПВО и для генерации этих моделей методами объектно-ориентированного проектирования.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.16.40 (0.01 с.) |

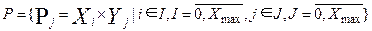 ,
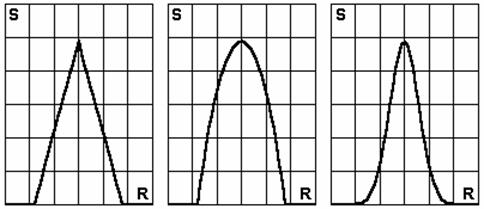
,
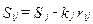 , (32)
, (32)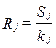 .
.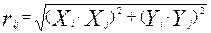 .
.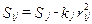 . (33)
. (33)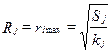 .
.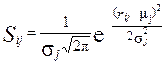 , (34)
, (34)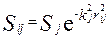 . (35)
. (35)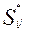 , при которой влиянием объекта можно пренебречь. Зададим эту величину как
, при которой влиянием объекта можно пренебречь. Зададим эту величину как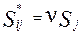 , (36)
, (36)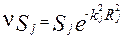
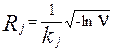 .
.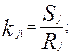
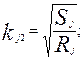
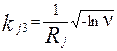 при n <1.
при n <1.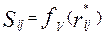 или трехмерного
или трехмерного 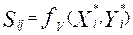 . Значения табличных величин
. Значения табличных величин 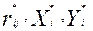 , как правило, задаются с большей дискретностью, чем значения
, как правило, задаются с большей дискретностью, чем значения 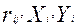 , соответствующие сетке ЭУ wi.
, соответствующие сетке ЭУ wi.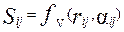 , (37)
, (37)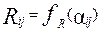 . (38)
. (38)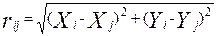 .
.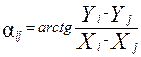 .
.

 законом влияния
законом влияния
 с симметричным законом влияния законом влияния
с симметричным законом влияния законом влияния

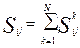 ,
,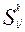 – величина влияния, определяемая k -й функцией
– величина влияния, определяемая k -й функцией 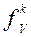 или k -й составляющей факторов влияния.
или k -й составляющей факторов влияния.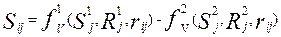 .
.


