
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез голографических фильтровСодержание книги Поиск на нашем сайте
Основной проблемой применения оптического коррелятора для решения задач распознавания объектов методом оптимальной фильтрации является трудность изготовления транспарантов, служащих комплексными пространственно-частотными фильтрами вида (3.1) или (3.7). В работах Вандер Люгта был предложен голографический метод создания согласованных пространственно-частотных фильтров. По существу, этот метод реализует возможность восстановления комплексной функции из спектральной плотности суммы этой функции с d- функцией. Он основан на формировании Фурье-образа:
вспомогательной функции:
и регистрации квадрата модуля этого Фурье-образа:
.
Последний член этого выражения пропорционален требуемой передаточной функции согласованного фильтра (3.9), причем наличие при нем линейного фазового множителя обеспечивает возможность пространственного отделения этого члена от остальных. По методу Вандер Люгта на фоточувствительном носителе регистрируется картина интерференции наклонного опорного параллельного пучка света (соответствует первому члену выражения (3.14) пучков света, дифрагированных на транспаранте объекта в оптическом Фурье-анализаторе (соответствует второму члену выражения (3.14)). Полученная таким образом голограмма Фурье используется в качестве пространственно-частотного фильтра, который устанавливается в частотную плоскость оптического коррелятора. Рассмотрим, каким образом в выходной плоскости коррелятора может быть сформировано требуемое корреляционное поле сравнения анализируемого и эталонного изображений с помощью голографического согласованного фильтра. Пусть транспарант, имеющий амплитудное пропускание, соответствующее функции опознаваемого объекта s(x,y), помещен в плоскости Р1 Фурье-анализатора (рисунок 3.2), Пусть плоскость Р1 в общем случае не совпадает с передней фокальной плоскостью линзы, но выполняется условие вида: z1=f’-z1, (3.16)
соответствующее случаю, когда плоскость транспаранта расположена между линзой и ее передней фокальной плоскостью. В плоскости Р3 помещен фоточувствительный материал. Под углом а к оптической оси в вертикальной плоскости направлен параллельный пучок света амплитуды А, служащий опорным. Пучок, освещающий входной транспарант, и опорный пучок предполагаются когерентными. Будем предполагать также отсутствие апертурных ограничений.
Рисунок 3.2 - Фурье-анализатор
При этих допущениях объект создает в плоскости Р3 следующее распределение амплитуд света:
где
Распределение амплитуд света от опорного пучка в плоскости Р3 имеет вид:
Общая интенсивность света, падающего на фоточувствительный материал, равна:
и с учетом (3.18)и (3.19)может быть представлена в виде:
Пропускание света по амплитуде для полученной голограммы определяется по формуле:
(3.20)
. Выражение (3.21) показывает, что процесс восстановления голограммы в оптическом Фурье-анализаторе должен приводить к появлению двух изображений объекта (прямого и сопряженного), разнесенных в разные стороны относительно светового пятна (нулевого дифракционного порядка), образованного светом, прошедшим голограмму без дифракции. Установим голограмму в частотную плоскость Р3' оптического коррелятора, показанного на рисунке 3.3 Будем считать, что плоскость Р1’ коррелятора находится на расстоянии z1- f' - dz1’ от линзы Л1’, плоскость Р3' от линзы Л1 - на расстоянии z3 = f ' - d z'3. Положим также, что линза Л2 имеет фокусное расстояние f², в общем случае отличное от фокусного расстояния f ' линзы Л1, а выходная плоскость коррелятора Р5' совпадает с фокальной плоскостью линзы Л2.
Рисунок 3.3 - Оптический коррелятор
В плоскость Р1¢ коррелятора поместим транспарант анализируемого изображения с объектом s(x,y), центрированным относительно оптической оси устройства. Вычислим распределение амплитуд света в выходной плоскости коррелятора:
(3.21)
Анализ последнего интеграла в выражении (3.22)показывает, что этот интеграл будет представлять собой автокорреляционную функцию опознаваемого объекта при условии устранения второго экспоненциального множителя в подынтегральном выражении. Устранение второго экспоненциального множителя в подынтегральном выражении (3.22 ) обеспечивается при условии:
т.е. при равенстве расстояний z1 и z1’. При выполнении этого условия распределение интенсивностей света в выходной плоскости коррелятора будет пропорционально квадрату модуля автокорреляционной функции объекта:
Эта функция будет иметь максимум в точке с координатами: р = f² sin a; q = 0, (3.24)
что соответствует направлению +1-го дифракционного порядка голограммы. Таким образом, в этом направлении выходной плоскости коррелятора достигается выходной эффект, аналогичный выходному эффекту устройств типа согласованных фильтров. Второй член функции пропускания голограммы-фильтра (3.21) будет отвечать в выходном распределении интенсивностей света функции, пропорциональной квадрату свертки функции объекта с собой. Эта функция центрирована относительно точки с координатами В начале координат выходной плоскости коррелятора возникает распределение интенсивности света от первого члена выражения (3.21), соответствующее нулевому дифракционному порядку голограммы. Исследовательский раздел
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.246 (0.007 с.) |

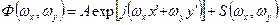 , (3.14)
, (3.14) , (3.15)
, (3.15)
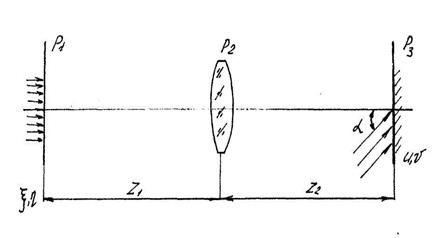
 (3.17)
(3.17)
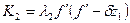 .
. . (3.18)
. (3.18) ,
, (3.19)
(3.19)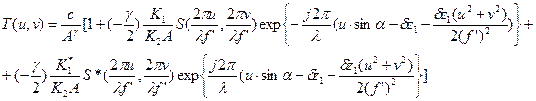


 ,(3.22)
,(3.22) (3.23)
(3.23) ; q = 0, и соответствует 1-му дифракционному порядку голограммы.
; q = 0, и соответствует 1-му дифракционному порядку голограммы.


