
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила округлення і виконання наближених обчисленьСодержание книги
Поиск на нашем сайте Точність обчислень завжди повинна відповідати точності вимірів. Зайва арифметична точність обчислень не позитивна якість, а недолік в роботі. Наприклад, якщо середнє арифметичне значення товщини пластинки після розрахунку було взято рівним 2,2543 мм при абсолютній похибці вимірів 0,03 мм, то при цьому показане лише невміння виконувати арифметичні дії з наближеними числами. Щоб не витрачати даремно часу для одержання сумнівної арифметичної точності, необхідно всі отримані величини перед підстановкою в формули округляти, залишаючи в них на одну значущу цифру більше, ніжу самої з наближених величин (з найменшим числом знаків). При округленні наближеного числа необхідно відкидати останні цифри, якщо перша з цифр, що відкидаються, менша 5, і додавати одиницю до попередньої цифри, якщо перша з цифр, що відкидаються, 5 або більше. За написаним числом, що виражає результат виміру або обчислення, можна говорити про ступінь точності. Значущі цифри – це усі цифри, крім нулів, що стоять перед числом, і нулів, поставлених наприкінці записаного результату замість відкинутих цифр при округленні. Десяткові таки числа – це усі цифри, розміщені праворуч від коми. Наприклад, число 25,002 має п'ять значущих цифр, а десяткових знаків три; число 0,0034 має дві значущі цифри, але чотири десяткових знаки. Якщо обчислення за наближеними даними проводяться у декілька дій, то в проміжних діях треба зберігати на одну значущу цифру більше в порівнянні з точністю визначуваних величин у даному досліді (тобто дві сумнівні цифри). У всіх арифметичних діях над наближеними числами в остаточному результаті треба уберігати стільки десяткових знаків, скільки їх мають наближені дані з найменшим числом десяткових знаків. Округлення чисел у процесі обчислення призводить до систематичної похибки. Відносна похибка, яку знаходять в результаті обчислень, має бути приблизно на порядок (тобто у 10 разів) менша за похибку результату непрямих вимірювань. У записі результату вимірювань залишають одну (максимум дві) сумнівні цифри. Похибку вимірювань округляють до однієї значущої цифри, якщо ця цифра не «1». Якщо ж ця цифра «1», то у похибці залишають дві значущі цифри, в записі результату вимірювань – дві сумнівні цифри. Сумнівними називаються значущі цифри в записі результату вимірювань, десяткові розряди яких збігаються з десятковими розрядами значущих цифр у записі похибки цього результату. Розряди останніх цифр Δx і x мусять співпадати. Для цього округляють x або приписують до нього невистачаючі нулі справа. Е округляють по тим же правилам, що і Δx. Спочатку округляють Δx, Δx=0,3 мм. Розряд останньої цифри Δx - десяті долі, а Знаходимо Е:
Кінцевий результат x = 173,6 ± 0,3 мм, α = 0,7, Е = 0,4 %
Похибки прямих вимірювань
Похибки прямих вимірювань визначаються за формулою
якщо деяку величину виміряти один раз. Якщо вимірювання виконувались n раз, то
В цих рівняннях t∞ - коефіцієнт Стьюдента для заданого a при необмеженому числі вимірів; d - похибка приладу; ν - похибка відліку, Наприклад: довжина тіла була виміряна 3 рази:
Відносна похибка дорівнює
Кінцевий результат: x = (13,3 ± 0,3) мм; α = 0,7; Е = 3,6 %.
Похибки непрямих вимірювань
Якщо y - величина, що вимірюється посередньо, її розраховують за відомою залежністю y=f(x1,x2,…xn) від змінних x1,x2,,…xn, які вимірюють безпосередньо. 1. Похибки непрямих вимірів визначаються за формулою:
якщо функціональна залежність досліджуваної величини є багаточлен. 2. Похибки непрямих вимірів можна визначати
якщо функціональна залежність досліджуваної величини є одночлен і потім знаходимо Dy як: 1. Якщо залежність функції
Тоді
2. Якщо залежність функції:
Тоді
У результаті отримуємо
Контрольні запитання
1. Дати визначення прямих і непрямих вимірів. Приклади. 2. За допомогою якої формули знаходять найбільш ймовірне значення виміряної величини? 3. Що таке відносна похибка? 4. Що називається випадковим відхиленням? 5. За якою формулою знаходять середнє квадратичне значення або похибку, викликану випадковими відхиленнями? 6. За якою формулою знаходять похибки засобів виміру. 7. За якою формулою знаходять похибки табличних величин та відліку. 8. Сформулюйте правила округлення. 9. Запишіть формули обчислення похибок при прямих вимірах. 10. Запишіть формули обчислення похибок при непрямих вимірах.
Література
1. Гончаренко С.У. Фізика: Підруч. для 11 кл. серед. загальноосв. шк..- К.: Освіта, 2002. – 319 с. 2. Гончаренко С.У. Фізика: Підруч. для 10 кл. серед. загальноосв. шк..- К.: Освіта, 2002. – 319 с. 3. Гончаренко С.У. Фізика: Пробн. навчальний посібник для ліцеїв та класів прородничо-наукового профілю. 10 клас.- К.: Освіта,1995.– 430с. 4. Гончаренко С.У. Фізика: Пробн. навч. посібник для 11 кл. ліцеїв та гімназій науково-природничого профілю.- К.: Освіта, 1995. – 448 с. 5. Коршак Є.В., Ляшенко О.І., Савченко В.Ф. Фізика. 11 кл.: Пробний підручник для загальноосвіт. шк. – К.: Ірпінь: ВТФ «Перун», 2000. – 232 с. 6. Коршак Є.В., Ляшенко О.І., Савченко В.Ф. Фізика. 10 кл.: Підруч. для загальноосвіт.навч. закл. – К.: Ірпінь: ВТФ «Перун», 2002. – 296с 7. Кирик Л.А. Фізика – 10. Різнорівневі самостійні та контрольні роботи. Харків: «Гімназія», 2002. – 192 с.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 – соті долі. Округляємо
– соті долі. Округляємо  = 73,6 мм.
= 73,6 мм.
 , n = 1, (18)
, n = 1, (18) , n > 1. (19)
, n > 1. (19) .
. =13,2
=13,2

 .
.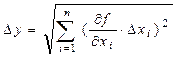 , (20)
, (20) , (21)
, (21) .
. . Наприклад:
. Наприклад: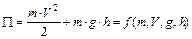 , тоді
, тоді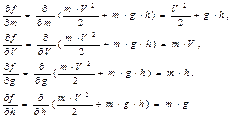
 .
.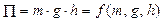 ,
,

 ,
, .
. .
.


