
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття теорії похибокСодержание книги
Поиск на нашем сайте
Числове значення будь-якої фізичної величини знаходять шляхом виміру, або розрахунку. Вимірювання це процес відшукання значення фізичної величини дослідним шляхом за допомогою спеціальних технічних засобів. Виміряти безпосередньо якусь фізичну величину цс означає порівняти її з деякою іншою однорідною з нею величиною, взятою за одиницю виміру. Отримане число показує, у скільки разів величина, що вимірюється, більше або менше обраної одиниці виміру. Отриманому числу приписується таке ж найменування, як і обраній одиниці. Прямі виміри здійснюються або шляхом безпосереднього порівняння фізичної величини, що вимірюється, з одиницями міри, як це має місце при вимірах довжини лінійкою, штангенциркулем, мікрометром і т.п., або приладами, градуйованими у визначених одиницях, наприклад амперметрами, вольтметрами і т.п. В багатьох випадках значення фізичної величини визначають за допомогою обчислень, використовуючи при цьому значення безпосередньо виміряних величин. Це трапляється тоді, коли відома функціональна залежність даної величини від безпосередньо виміряних величин. Наприклад, для визначення об’єму циліндра використовують функціональну залежність від діаметра d та висоти h:
При непрямих вимірах, величину y знаходять по відомій функціональній залежності y = f(x1, x2,...,xn) від величин x1, x2, … xn, значення котрих знаходять прямими вимірами. Виміряне значення фізичної величини завжди відрізняється від істинного тому, що при вимірюваннях завжди виникають похибки. При вимірюваннях необхідно знайти не тільки наближене значення фізичної величини, але й обчислити відхилення цього значення від істинного. Цим питанням займається теорія похибок. Всі вимірювання можуть бути виконані тільки з визначеним ступенем точності. Похибка вимірювань визначається як відхилення результату виміру від істинного значення величини. Як показує теорія і практика, до істинного значення вимірюваної величини найближче підходить середнє арифметичне значення багатьох вимірювань. Якщо якусь величину х виміряли n раз і отримали ряд значень х1, х2... хn, то найбільш ймовірне значення виміряної величини х знаходять як середнє арифметичне результатів окремих вимірів:
Похибки вимірів бувають систематичними, випадковими і промахами. Систематична похибка – це складова частина похибки виміру, що залишається сталою, або такою, що закономірно змінюється при повторних вимірах однієї та тієї ж величини. Випадкова похибка – це складова частина похибки вимірювань, що змінюється випадково при повторних вимірах однієї та тієї ж величини. Промах – це такий результат виміру, значення якого набагато відрізняється від очікуваної похибки в даних умовах. Наприклад, ці похибки можуть бути отримані, якщо прилад несправний або якщо експериментатор неуважний. Похибки вимірювань бувають абсолютними і відносними. Абсолютною похибкою вимірювання називається похибка, виражена в одиницях величини, що вимірюється, вона визначається формулою
де х – значення, здобуте при вимірюванні; Х – справжнє значення величини, що вимірюється (найбільш ймовірне). Середня арифметична абсолютна похибка n вимірювань дорівнює
Величина
де Δx – абсолютна похибка вимірювань x. Чим більша ширина інтервалу 2Δx, тим більшою буде ймовірність того, що точне значення вимірюваної величини належить цьому інтервалу. Відносною похибкою вимірювання називається відношення абсолютної похибки вимірювання до справжнього значення величини що вимірюється
як правило, визначається у відсотках
Знайти істинне значення фізичної величини х неможливо. Можна тільки вказати на інтервал (хmin, хmax), в якому з ймовірністю a знаходиться значення досліджуваної величини. Приклад: поглядом вимірюють зріст студента в сантиметрах. Ми можемо припустити, що зріст студента може бути визначений між 1,5 м і 2,0 м з ймовірністю 0,9. Тоді ми можемо стверджувати, що зріст студента може бути визначений між 1,6 м і 1,8 м з меншою ймовірністю 0,6 і так далі. Цей інтервал називають довірчим інтервалом. На рис.1.1 зображено довірчий інтервал досліджуваної величини x, де
з ймовірністю a, або
Рисунок 1 Ймовірність знаходження істинного значення вимірюваної величини в інтервалі
і збільшують її в t раз (t – так званий коефіцієнт Ст`юдента. Цей коефіцієнт було введено в 1908 році англійським математиком та хіміком В.С. Госсетом). Величину
називають випадковим відхиленням. Середнє квадратичне похибка результату серії вимірювань, викликана випадковими відхиленнями Dxi, визначається як
Множимо знайдене значення коефіцієнта Стьюдента t (коефіцієнт Стьюдента, залежить від a і кількості вимірів n) на середню квадратичну похибку середнього значення, знаходимо випадкову похибку Δхвип результатів прямих вимірювань
Таблиця 1
Похибки засобів вимірювання
До засобів вимірювань належать вимірювальні прилади та установки. Кожен прилад дає похибку, так як його неможливо зробити ідеальним. Похибка засобів вимірювання не перевищує деякої величини. Цю величину називають межею основної допустимої похибки вимірювального приладу (МОДП). МОДП на засоби вимірювання встановлюється державними стандартами і визначається у вигляді абсолютних, відносних та приведених похибок. Абсолютна похибка приладу d – це є різниця
де a – показання приладу, X – справжнє значення вимірюваної величини. Взагалі d дорівнює ціні найменшої поділки інструмента. Наприклад: для лінійки d =1 мм. Відносна похибка вимірів – це відношення
Як правило, вона визначається у відсотках
Приведена похибка вимірювання або клас точності визначається відношенням
і визначається у відсотках. D – максимальне значення шкали інструмента. Наприклад: сила струму вимірюється амперметром з діапазоном 0 ÷ 1 А, клас точності 0,5. Це означає, що Хн = 1 А; γ = 0,5 % і
Якщо амперметр показує 0,3 А, тоді
Похибки табличних величин
1. Похибка табличної величини визначається за формулою
де a - довірча ймовірність; ν - половина ціни розряду останньої залишеної цифри табличної величини. Наприклад: величина π дорівнює 3,14. В цьому випадку ν = 0,005 і
Якщо величина π дорівнює 3,141 і ν = 0,0005, то
2. При користуванні вимірювальними приладами виникають похибки відліку. Типово, похибка відліку дорівнює половині ціни поділки шкали приладу. Наприклад: лінійка має похибку відліку ν = 0,5 мм.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.4.135 (0.01 с.) |

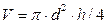 .
. . (1)
. (1)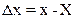 , (2)
, (2) . (3)
. (3) визначає інтервал, у межах якого з певною ймовірністю знаходиться істинне значення вимірюваної величини. За визначенням
визначає інтервал, у межах якого з певною ймовірністю знаходиться істинне значення вимірюваної величини. За визначенням ., (4)
., (4) , (5)
, (5) . (6)
. (6)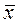 – найбільш ймовірне значення виміряної величини; Δх – півширина довірчого інтервалу для заданого a. Тому, істинне значення вимірюваної величини може бути визначене як
– найбільш ймовірне значення виміряної величини; Δх – півширина довірчого інтервалу для заданого a. Тому, істинне значення вимірюваної величини може бути визначене як , (7)
, (7)
 Dx залежить від кількості вимірювань n. Якщо
Dx залежить від кількості вимірювань n. Якщо  , то ймовірність наближається до 1. Якщо ж n дорівнює кільком одиницям, то ймовірність не досягає й 0,6. Тому для малої кількості вимірювань згаданий інтервал розширюють, збільшуючи Δx. Для цього знаходять середньоквадратичну похибку середнього арифметичного
, то ймовірність наближається до 1. Якщо ж n дорівнює кільком одиницям, то ймовірність не досягає й 0,6. Тому для малої кількості вимірювань згаданий інтервал розширюють, збільшуючи Δx. Для цього знаходять середньоквадратичну похибку середнього арифметичного , (9)
, (9) , (10)
, (10)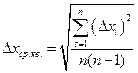 . (11)
. (11)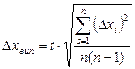 . (12)
. (12)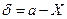 , (13)
, (13)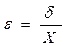 . (14)
. (14) . (15)
. (15) , (16)
, (16) .
.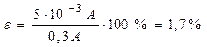 .
. , (17)
, (17)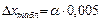 .
. .
.


