
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет искажений при замене участка сферы плоскостьюСодержание книги
Поиск на нашем сайте Искажение расстояний Небольшой участок сферической поверхности при определенных условиях можно принять за плоскость. Применение модели плоской поверхности при решении геодезических задач возможно лишь для небольших участков поверхности Земли, когда искажения, вызванные заменой поверхности сферы или эллипсоида плоскостью невелики и могут быть вычислены по простым формулам. Это тем более оправдано, если учесть, что измерения на местности и чертежные работы всегда выполняются с ошибками, а потому небольшую часть сферы (эллипсоида), отличающуюся от плоскости на величину, меньшую ошибок измерений, можно считать плоской. Рассчитаем, какое искажение получит дуга окружности, если заменить ее отрезком касательной к этой дуге. На рис.1.7 точка O - центр окружности, дуга ABC радиусом R стягивает центральный угол ε. Проведем касательную через середину дуги в точке B и, продолжив радиусы OA и OC до пересечения с касательной, получим точки A' и C'.
Рис.1.7 Пусть дуга ABC имеет длину D, а отрезок касательной A'C' - длину S. Известно, что для окружности D = R* ε, причем угол ε должен быть выражен в радианах. Из ΔOBC' имеем: S/2=R*tg(ε/2) или S = 2 R tg(ε/2) (1.1) Разность (S - D) обозначим через ΔD и напишем ΔD=R*[2*tg(ε/2)- ε] (1.2) Разложим tg(ε/2) в ряд, ограничившись ввиду малости угла ε/2 двумя членами разложения,
Подставим это выражение в формулу (1.2) и получим
Но ε = D/R, поэтому
Отношение ΔD/D называется относительным искажением длины дуги при замене ее отрезком касательной, оно будет равно:
Подсчитаем конкретные значения относительного искажения для раз ных длин дуги D (R = 6400 км): D = 20 км, Δ D/D = 1/1 218 000, Достигнутая точность измерения расстояний пока не превышает 1/1 000 000, поэтому при геодезических работах любой точности участок сферы 20 х 20 км2 можно считать плоским. При работах пониженной точности размеры участка сферы, принимаемого за плоскость, можно увеличить. Искажение высот точек Если заменить небольшой участок сферы касательной плоскостью, то будут искажены не только длины линий, но и отметки точек. Изменения отметок симметричны относительно точки B и зависят от удаления от этой точки; обозначим отрезок BC', равный половине отрезка A'C', через s. Отметка точки C', находящейся на плоскости, отличается от отметки точки C, лежащей на сфере, на величину отрезка CC'=p (рис.1.7). Из треугольника OBC' следует: R2 + s2 = (R + p)2, откуда получаем:
В знаменателе величина p намного меньше величины 2*R, поэтому, отбросив ее, мы допустим несущественную ошибку. Таким образом,
Влияние кривизны Земли на отметки точек нужно учитывать при любых расстояниях между точками; например, при s=10 км p=7.8 м и при s=100 м p=0.8 мм. 1.6. Понятие о плане, карте, аэроснимке Уменьшенное изображение на бумаге горизонтальной проекции небольшого участка местности называется планом. На плане местность изображается без заметных искажений, так как небольшой участок поверхности относимости можно принять за плоскость. Если участок поверхности относимости, на который спроектирована местность, имеет большие размеры, то при изображении его на плоскости неизбежны заметные искажения длин линий, углов, площадей. Просто развернуть на плоскость участок сферы или эллипсоида без разрывов и складок нельзя, поэтому приходится прибегать к помощи математики. Математически определенный способ изображения поверхности сферы или эллипсоида на плоскости называется картографической проекцией; каждой точке Mo (φ, λ или B, L) изображаемой поверхности соответствует одна точка M (x, y) плоскости. Аналитически картографическая проекция задается двумя уравнениями x = f1(φ, λ), y = f2(φ, λ), где f1 и f2 - функции независимые, непрерывные, однозначные и конечные. Картографические проекции классифицируются по:
Картой называется уменьшенное изображение на бумаге горизонтальной проекции участка земной поверхности в принятой картографической проекции, то-есть, с учетом кривизны поверхности относимости. В нашей стране топографические карты составляются в поперечно-цилиндрической равноугольной проекции Гаусса. Масштабом карты (плана) называется отношение длины отрезка на карте (плане) к горизонтальной проекции соответствующего отрезка на местности. По своему назначению все географические карты делятся на общегеографические и тематические. На общегеографических картах показывают рельеф, гидрографию, растительный покров, населенные пункты, пути сообщения, различные границы и другие объекты природного, хозяйственного и культурного назначения. На тематических картах изображают размещение, сочетание и связи различных природных и общественных явлений; известны геологические, климатические, ландшафтные, экологические карты, карты полезных ископаемых, карты размещения производительных сил, карты населения, исторические, учебные, туристические и др. Крупномасштабные (масштаба 1: 1 000 000 и крупнее) общегеографические карты называются топографическими. Они издаются в виде отдельных листов размером примерно 40 см x 40 см.
Рис.1.8 Аэроснимок - это фотографическое изображение участка земной поверхности, представляющее его центральную проекцию. При отвесном положении оси фотоаппарата получается плановый снимок, при наклонном - перспективный снимок. Масштабом аэроснимка называется отношение длины отрезка на аэроснимке к длине соответствующего отрезка на местности (рис.1.8). Масштаб аэроснимка определяют по формуле:
где: f - фокусное расстояние фотоаппарата, f = OC',
|
||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.175 (0.007 с.) |


 или
или  .
.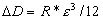 .
. .
. (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5)
 (1.6)
(1.6)


