Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсных материалов методом касательныхСодержание книги
Поиск на нашем сайте
Склонность к самовозгоранию является свойством вещества, проявляющимся в способности загораться при отсутствии внешнего источника зажигания за счет внутренних экзотермических реакций. Современные методы определения склонности веществ к самовозгоранию основаны на анализе кривых температура-время или критических условий самовозгорания. Наибольшее распространение получили термографические методы. Критические условия при тепловом самовозгорании и самовоспламенении можно записать предельным равенством адиабатической скорости самонагревания
Равенство (3.1) справедливо для образцов с различными темпами охлаждения. Поэтому, определив критические температуры самовозгорания нескольких образцов (не менее 4-5), при известных их темпах охлаждения методом касательных можно определить кинетические параметры Е и С, методика определения которых состоит в следующем. Экспериментально определяют несколько (не менее 4-5) критических температур самовозгорания При тепловом механизме самовозгорания эта зависимость описывается экспонентой Аррениуса
Кинетические параметры Е и С, входящие в это уравнение, определяют следующим образом. Значение координат точек касания графиков самонагревания По этим точкам в координатах: обратная температура (ось Х) – натуральный логарифм адиабатической скорости самонагревания (ось Y) строят прямую
С помощью построенного графика энергию активации Е рассчитывают по формуле:
Затем значение Е подставляют в (3.2) и вычисляют Порядок расчета Е и С методом касательных рассмотрен ниже на конкретном примере.
УСЛОВИЕ ЗАДАЧИ № 3 Определить кинетические параметры энергии активации ( Е) и предэкспоненциального множителя (С) в уравнении Аррениуса по критическим условиям самовозгорания твердых дисперсных материалов методом касательных. Исходные данные для решения задачи приведены в таблице 3.1.
Таблица 3.1 Исходные данные
Примечание: Построение графиков производится на миллиметровой бумаге, которая вклеивается в тетрадь КОНТРОЛЬНЫЙ ПРИМЕР Для того чтобы построить график адиабатической скорости самонагревания в координатах Например: Вариант n
Рис. 3.1 Чтобы провести прямые охлаждения, необходимо проделать следующее графические и арифметические действия: - взять - отложить на оси - восстановить из полученных точек перпендикуляры к оси - найти произведения - отложить вертикально вверх на соответствующих перпендикулярных прямых полученные значения Принимаем
Рис 3.2 Находим произведения первая точка: вторая точка: третья точка: четвертая точка: пятая точка: Откладываем вверх по вертикали полученные значения, причем масштаб по вертикальной оси выбирается таким образом, чтобы от последнего полученного значения ( Через две точки строим прямые охлаждения по уравнению
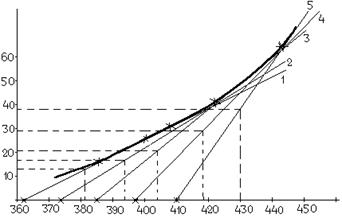
Рис 3.3 После этого строим кривую температурной зависимости адиабатической скорости самонагревания Кривая адиабатической скорости самонагревания строиться следующим образом. На прямых охлаждения (1, 2, 3, 4 и 5) определяем при помощи лекала возможные точки касания экспоненты и намечаем их координаты. Так для прямой охлаждения 1 экспонента коснется в точке
Рис 3.4. График температурной зависимости адиабатической скорости самонагревания Через эти точки проводим по лекалу касательную, получаемую в виде экспоненты, которая описывается зависимостью (3.1). Координаты получаемых точек касания кривой адиабатической скорости самонагревания с прямыми охлаждения заносим в таблицу 3.2.
Таблица 3.2
Путем вычислений заполняем оставшиеся две графы таблицы 3.2 по нижеприведенным соотношениям: 1. 2. Результаты вычислений заносим в последние две графы таблицы 3.3. Таблица 3.3
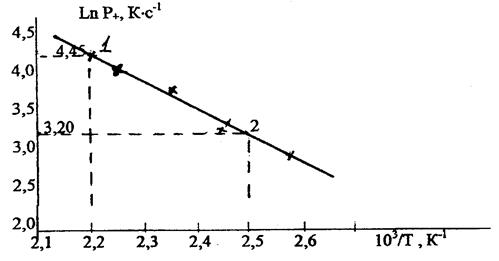
По данным последних двух колонок (табл. 3.3) строим график в координатах Ln(
Рис. 3.5
По полученным на графике (рис. 3.5) точкам строим прямую. Затем на этой прямой выбираем две характерные точки (любые) и координаты этих точек подставляем в следующие соотношения: 1. 2. откуда находим С:
Рис. 3.6. График адиабатической скорости самонагревания в координатах Аррениуса
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 критической температуре
критической температуре  и виртуальной скорости охлаждения
и виртуальной скорости охлаждения 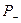 в стадии регулярного теплового режима первого рода (
в стадии регулярного теплового режима первого рода (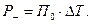 ) при этой же температуре (
) при этой же температуре (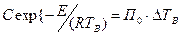 (3.1)
(3.1) образцов (навесок) с различными темпами охлаждения
образцов (навесок) с различными темпами охлаждения  . Численное значение критических температур
. Численное значение критических температур  ), с тангенсами, равными темпам охлаждения (
), с тангенсами, равными темпам охлаждения ( ). Затем проводят огибающую кривую таким образом, чтобы она по возможности касалась всех графиков охлаждения. Согласно теории теплового самовозгорания эта кривая является графиком искомой функции
). Затем проводят огибающую кривую таким образом, чтобы она по возможности касалась всех графиков охлаждения. Согласно теории теплового самовозгорания эта кривая является графиком искомой функции  , описывающей температурную зависимость адиабатической скорости самонагревания.
, описывающей температурную зависимость адиабатической скорости самонагревания.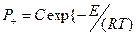 .
. заносят в таблицу.
заносят в таблицу. (3.2)
(3.2) (3.3)
(3.3) .
. ) и отложить на горизонтальной оси
) и отложить на горизонтальной оси 




 (произвольно, любое целое число);
(произвольно, любое целое число); (полученных значений будет также пять);
(полученных значений будет также пять); .
. ºС и отложим на оси
ºС и отложим на оси  (рис. 3.2).
(рис. 3.2).
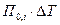 :
: ;
; ;
;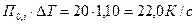 ;
; ;
; ;
; ) оставалось ½ тетрадного листа (рис 3.2).
) оставалось ½ тетрадного листа (рис 3.2). на перпендикуляре о381 К. Так получаем прямую охлаждения 1 (см. рис. 3.3). Аналогично строим прямые охлаждения для 2, 3, 4 и 5 прямой.
на перпендикуляре о381 К. Так получаем прямую охлаждения 1 (см. рис. 3.3). Аналогично строим прямые охлаждения для 2, 3, 4 и 5 прямой.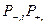 К/с
К/с Т, К
Т, К . Эта кривая должна проходить таким образом, чтобы она касалась прямых охлаждения только в одной точке и не пересекала этих прямых (рис 3.4);
. Эта кривая должна проходить таким образом, чтобы она касалась прямых охлаждения только в одной точке и не пересекала этих прямых (рис 3.4); ,
,  ; для прямой 2 ―
; для прямой 2 ―  ,
,  ; для прямой 3 ―
; для прямой 3 ―  ,
,  ; для прямой 4 ―
; для прямой 4 ― 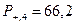 ,
, 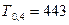 ; для прямой 5 ―
; для прямой 5 ―  ,
,  .
. Т, К
Т, К
 , К/с
(из графика)
, К/с
(из графика)
 (расчетом)
(расчетом)