
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение критической температурыСодержание книги
Поиск на нашем сайте
САМОВОЗГОРАНИЯ СКОПЛЕНИЯ САМОНАГРЕВАЮЩЕГОСЯ ТВЕРДОГО ДИСПЕРСНОГО МАТЕРИАЛА Теория теплового самовозгорания (самовоспламенения) позволяет решить прямую и обратную задачу самовозгорания: - по кинетическим параметрам определить критические условия самовозгорания (критические температуры То и Тв); - по критическим условиям определить кинетические параметры (Е и С). Эти задачи можно решать аналитически и графически. Рассмотрим графический способ определения критической температуры самовозгорания ( Известно [3, 4], что соотношение между энергией активации (Е) и логарифмом предэкспоненциального множителя (ln С) определяется компенсационным уравнением: Е = где R - универсальная газовая постоянная, R=8,314 Дж·моль-1·К-1;
Величина
где Из уравнения (2.1) имеем:
Из выражения (2.3) определяется величина предэкспоненциального множителя С и сравнивается с экспериментальным значением данного материала. Далее проводится расчет адиабатической скорости самонагревания (
При известных значениях С и Е, задаваясь температурами ( Результаты расчета На следующем этапе строится график теплоотвода по уравнению:
где
где
F - поверхность скопления материала,
V - объем скопления, Коэффициент неравномерности нагрева определяют по формуле:
где
Затем проводится прямая охлаждения под углом
УСЛОВИЕ ЗАДАЧИ № 2 Определить критические температуры самовозгорания (То и Тв) для скопления самонагревающегося твердого дисперсного материала, используя данные, приведенные в таблице 2.1. Таблица 2.1 Исходные данные
КОНТРОЛЬНЫЙ ПРИМЕР Условие задачи Определить критические температуры самовозгорания (
При этом:
Решение: Используя выражение (2.2), определяем адиабатическую скорость самонагревания при температуре Тс:
Далее, из уравнения (2.3), находим
или Вычисленное значение
По уравнению (2.4) проводим расчет адиабатической скорости самонагревания Таблица 2.2 Адиабатические скорости самонагревания
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.158.29 (0.009 с.) |

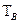 ) скопления твердого дисперсного материала.
) скопления твердого дисперсного материала. (2.1)
(2.1) - температура компенсации,
- температура компенсации,  ;
; - адиабатическая скорость самонагревания при температуре Тс,
- адиабатическая скорость самонагревания при температуре Тс, 
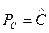 exp
exp  (2.2)
(2.2)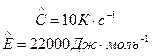 } изокинетические параметры.
} изокинетические параметры.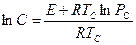 (2.3)
(2.3) ) для конкретного материала по уравнению Аррениуса:
) для конкретного материала по уравнению Аррениуса: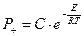 (2.4)
(2.4) ), находят
), находят 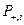 .
.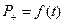 . Для удобства построения графика значения
. Для удобства построения графика значения 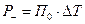 , (2.5)
, (2.5) - темп охлаждения. Его вычисляют по формуле:
- темп охлаждения. Его вычисляют по формуле: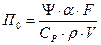 (2.6)
(2.6)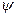 - коэффициент неравномерности нагрева;
- коэффициент неравномерности нагрева;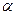 - коэффициент теплоотдачи от поверхности скопления к окружающей среде,
- коэффициент теплоотдачи от поверхности скопления к окружающей среде,  ;
; ;
; - теплоемкость материала,
- теплоемкость материала, 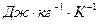 ;
;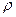 - плотность материала,
- плотность материала, 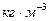 ;
; .
. (2.7)
(2.7) - относительный градиент
- относительный градиент 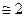 ;
;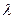 - коэффициент теплопроводности материала,
- коэффициент теплопроводности материала,  ;
;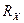 - определяющий размер (расстояние от поверхности материала до теплофизического центра), м.
- определяющий размер (расстояние от поверхности материала до теплофизического центра), м. и
и  .
.


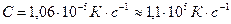 , что соответствует
, что соответствует  .
. (
( ) сравниваем по секторной диаграмме (рис. 2.2) с экспериментальным значением. Это соответствует древесно-растительным материалам (при
) сравниваем по секторной диаграмме (рис. 2.2) с экспериментальным значением. Это соответствует древесно-растительным материалам (при 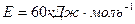 и
и 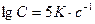 ).
).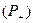 в зависимости от температуры (Т, К). Результаты расчетов заносим в табл. 2.2 и
в зависимости от температуры (Т, К). Результаты расчетов заносим в табл. 2.2 и 


