Ибятов Р.И, Нурсубин М.С., Валиев А.А.

 

 

Программирование и офисные

Приложения Windows

 

 

Методическое пособие и контрольные задания

студентам-заочникам всех специальностей

 

 

Казань 2011

УДК 681.3.06 (07)

ББК 32.973-01С

 

Составители:

Ибятов Р.И., д.т.н., профессор, заведующий кафедрой;

Нурсубин М.С., к.т.н., доцент;

Валиев А.А., старший преподаватель.

 

Рецензенты:

Заведующий кафедрой системотехники КГТУ (КХТИ),

д.т.н., профессор Н.Н. Зиятдинов

Старший преподаватель кафедры экономической кибернетики

Казанского ГАУ, к.э.н. А.Р. Зиятдинова

 

Печатается по решению учебно-методической комиссии Института экономики, протокол № 11 от 05.04.2011г. и кафедры прикладной информатики и математики, протокол № 7 от 25.03.2011г.

 

Программирование и офисные приложения Windows: Методическое пособие и контрольные задания студентам-заочникам всех специальностей/ Казанский ГАУ. Р.И. Ибятов, М.С. Нурсубин, А.А. Валиев. Казань, 2011. 60 с.

 

 

Настоящее методическое пособие предназначено для студентов – заочников всех специальностей, изучающих предметы «Информатика», «Информатика и программирование». Методическое пособие содержит краткий теоретический материал, образцы решения задач и контрольные задания.

 

 

УДК 681.3.06 (07)

ББК 32.973-01С

 

 

© Казанский государственный аграрный университет 2011 г

Методические указания для выполнения

Контрольной работы

АРИФМЕТИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА

Системы счисления

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Система счисления – это совокупность приемов и правил, по которым числа записываются и читаются.

Существуют позиционные и непозиционные системы счисления. Непозиционные системы счисления возникли раньше позиционных систем. В них значение цифры не зависит от ее позиции в записи числа. Самой распространенной из непозиционных систем счисления является римская. В качестве цифр в ней используются буквы латинского алфавита:I – 1; V – 5; X – 10; L – 50; C – 100; D- 500; M – 1000.

Величина числа определяется как сумма или разность цифр в числах. Если меньшая цифра стоит слева от большей, то она вычитается, если справа то прибавляется. Например:

XXIV = 10+10+(5-1) =24,

MCMLVIII = 1000 + (1000-100) + 50+5 +1+1+1=1958.

В позиционных системах счисления значение цифры зависит от ее положения в числе. Например, в десятичном числе 525,5 первая пятерка означает 5 сотен, вторая – 5 единиц, а третья – 5 десятых долей единицы. Сама же запись числа 525,5 означает сокращенную запись суммы:

525,5= 500+ 20+5+0.5 = 5 * 10² + 2 * 10¹ + 5 * 10⁰ + 5 * 10^-1. (1.1)

Любая позиционная система счисления характеризуется своим основанием, которое указывает на количество различных цифр, используемых для изображения чисел в данной системе счисления. Например, в десятичной системе счисления используется десять всем хорошо известных чисел: 0,1,2,3,4,5,6,7,8,9., поэтому основанием является число 10. В записи (1.1) число 525,5 разложено по основанию 10.

Для сохранения и распознавания информации самым простым являются технические устройства, которые имеют два устойчивых состояния:

- перфорированные ленты и карты (пробито / непробито);

- электромагнитные реле (замкнуто / разомкнуто);

- участок поверхности магнитного носителя информации (намагничен / размагничен);

- участок поверхности лазерного диска (отражает / неотражает);

- напряжение в элементах электронных схем (значительное / отсутствует).

Поэтому в компьютере для предоставления информации используется двоичное кодирование, а арифметическую основу компьютера составляет двоичная система счисления.

В двоичной системе счисления основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. Например, развернутая запись двоичного числа 101,01 может выглядеть так:

101.01 = 1*2²+0*2¹+1*2⁰+0*2^-1+1*2^-2.

Возможно использование множества позиционных систем счисления. Например, в компьютерах для уменьшения разряда числа используется восьмеричная (0,1,2,3,4,0,1,2,3,4,5,6,7) и шестнадцатеричная (0,1,2,3,4,5,6,7,7,8,9, A,B,C,D,E,F) системы. В общем случае в q -ичной системе счисления запись числа A_q = a_n-1a_n-2….a₁a₀,a _-1a _-2…..a _–m, которое содержит n целых разрядов числа и m дробных разрядов числа, выглядит так:

A_q=a_n-1*q^n-1+a_n-2*q^n-2+…+a₀*q⁰+a_-1*q^-1+…+a_-m*q^-m

Коэффициенты а_i в этой записи являются цифрами числа, записанного в q -ичной системе счисления.

 

Перевод чисел из десятичной системы счисления

В двоичную и обратно

Для перевода целого десятичного числа N в двоичную систему счисления необходимо разделить N на 2 с остатком. Затем неполное частное, полученное от этого деления, нужно снова разделить на 2 с остатком и т.д., пока последнее полученное неполное частное не станет равным нулю. Число N в двоичной системе счисления представится в виде упорядоченной последовательности полученных остатков деления, записанных в порядке, обратном порядку их получения.

 

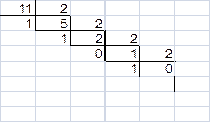
Пример 1.2.1. Перевести числа 25 и 11 из десятичной системы в двоичную.

 

 

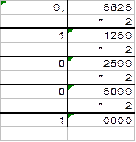
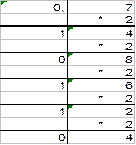
В результате делений получили: 27₁₀=11001₂ и 11₁₀=1011₂. Ответы проверим обратным переводом:

11001₂= 1*2⁴+1*2³+0*2²+0*2¹+1*2⁰=16+8+0+0+1=25₁₀;

1011₂= 1*2³+0*2²+1*2¹+1*2⁰= 8+0+2+1=11₁₀.

Для перевода правильной десятичной дроби F в двоичную систему счисления необходимо F умножить на 2, затем дробную часть полученного произведения снова умножить на 2 и т.д., до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность изображения числа F в двоичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения.

Пример 1.2.2. Перевести числа 0,5625 и 0,7 в двоичную систему.

и.т.д.

В результате умножений получили: 0,5625₁₀=0,1001₂ и 0,7 0,10110₂. Как видим, во втором примере процесс умножения может продолжаться бесконечно, давая всё новые и новые знаки в изображении двоичного эквивалента числа 0,7. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется 2^-(к+1)/2.

 

Ответы проверим обратным переводом:

0,1001₂=1*2^-1+0*2^-2+0*2^-3+1*2^-4=1/2+0+0+1/16=9/16=0,5625;

0,1011₂=1*2^-1+0*2^-2+1*2^-3+1*2^-4=1/2+0+1/8+1/16=11/16= 0,6875₁₀ 0,7.

Перевод произвольных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно – дробная, в итоговой записи полученного числа целая часть отделяется от дробной запятой.

 

Пример 1.2.3. Перевести число 111,5625 в двоичную систему.

В примерах 1.2.1 и 1.2.2 были установлены, что 11₁₀=1011₂ и 0,5625₁₀= 0,1001₂. Поскольку 11,5625=11₁₀+0,5625₁₀, то получим 11,5625₁₀=1011,1001₂.