
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класифікація подій ,класичне означення ймовірності випадкової події ,статистичне означення ймовірності;елементи комбінаторики ;аксіоми теорії ймовірностей та їх наслідки.Содержание книги
Поиск на нашем сайте Предмет курсу. Класифікація подій,класичне означення ймовірності випадкової події,статистичне означення ймовірності;елементи комбінаторики;аксіоми теорії ймовірностей та їх наслідки. Випробування — реальний або мислений експеримент (виконуваний за певної незмінної сукупності умов), результати якого піддаються спостереженню. Подія — результат випробування. Якщо в результаті випробування деяка подія неодмінно відбудеться, то вона називається достовірною і позначається літерою U. Подія, яка в даному випробуванні не може відбутись, називається неможливою і позначається літерою V. Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. Випадкові події позначаються літерами A, B, C, D, … Класичною імовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій, що утворюють простір елементарних подій W: P(A)= m /n. Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: W(A)= m /n. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин обчислюється за формулою: Pn = n! Розміщенням із n елементів по m (0 Комбінаціями з n елементів по m (0 Система подій називається алгеброю подій, якщо: 1. 2. із того, що Числова функція P, що визначена на системі подій Q, називається ймовірністю, якщо: 1. Q є алгеброю подій; 2. для будь-якого A Ì Q існує P(A)³0; 3. P(W)= 1; 4. якщо А і В є несумісними (АÇВ)=Æ, то P(AÈB)=P(A)+P(B); 5. для будь-якої спадної послідовності
Q,
Трійка (Q,W,R), де Q є алгеброю подій і Р задовольняє аксіоми 1-5, називається простором імовірностей. Наслідки аксіом: 1. якщо випадкові події 2. якщо випадкові події 3. формула додавання для n сумісних 4. якщо випадкова подія А сприяє появі В(АÌВ), то P(A)£P(B) Залежні й незалежні випадкові події, формули додавання ймовірностей. Події В і С називаються залежними, якщо ймовірність однієї з них змінюється залежно від того, відбулась друга подія чи ні. У противному разі події називаються незалежними. Нехай подія А є сумою двох подій В і С. Тоді: а) якщо події В і С несумісні, то P(A)=P(BÈC)=P(B)+P(C); б) якщо події В і С сумісні, то P(A)=P(BÈC)=P(B)+P(C)-P(BÇC).
Умовна ймовірність та її властивості. Імовірність події A, визначена за умови, що подія В відбулася, називається умовною і позначається P(A/B). P(A/B)= P(A 1. P(A/B)=0, якщо AÇB=Æ 2. P(A/B)=1, якщо AÇB=B 3. у решті випадків 0<P(A/B)<1. Формули множення ймовірностей для залежних та незалежних випадкових подій. Нехай подія А є добутком двох подій В і С. Тоді: а) якщо події В і С незалежні, то P(A)=P(BÇC)=P(B)*P(C); б) якщо події В і С залежні, то P(A)=P(BÇC)=P(B)*P(C/B). Формула повної ймовірності та формула Байеса. Нехай подія А може відбутися тільки за умови настання однієї із несумісних подій
де Наведена залежність називається формулою повної ймовірності. Подія А може відбутись одночасно з деякою із подій
Закон розподілу Пуассона Дискретна випадкова величина має розподіл Пуассона, якщо вона набуває зліченної множини значень Якщо у схемі незалежних повторних випробувань n велике і р або 1 – р прямують до нуля, то біноміальний розподіл апроксимується розподілом Пуассона, коли Ймовірна твірна 25. Числові характеристики розподілу Біноміального закону розподілу: Імовірності в цьому законі визначаються за формулою
Рівномірний закон розподілу Якщо ймовірність потрапляння випадкової величини на інтервал пропорційна до довжини інтервалу і не залежить від розташування інтервалу на осі, то вона має рівномірний закон розподілу. Щільність такого розподілу:
Рівномірний закон розподілу легко моделювати. За допомогою функціональних перетворень із величин, розподілених рівномірно, можна діставати величини з довільним законом розподілу. Числові характеристики розподілу:
27. Нормальний закон розподілу задається щільністю
Часто застосовується також формула:
Теорема Чебишова Нехай 1.M(Xі)>= aі 2.D(Xі )<= с Для всіх і=1,2,3…..n Якщо випадкові величини у послідовності Ця теорема є законом великих чисел,так само як і центральна гранична теорема Теорема Бернулі Нехай проводиться n незалежних повторних випробувань, у кожному з яких імовірність настання події А дорівнює р.Якщо ймовірність появи випадкової події А в кожному з незалежних випробувань n є величиною сталою і дорівнює P,то при необмеженому збільшенні числа експериментів n→∞ Імовірність відхилення відносної частоти появи випадкової події W(A) від імовірності p,взятої за абсолютною величиною на ε(ε>0) прямуватиме до одиниці зі зростанням n,що можна записати так:
де Наведена теорема є законом великих чисел,так само як і центральна гранична теорема 37) Центральна гранична теорема. Для послідовності випадкових величин
Теорема. Якщо випадкові величини в послідовності незалежні, однаково розподілені і для них існують моменти другого порядку, то
тобто граничним розподілом для Теорема Ляпунова. Якщо для незалежних випадкових величин, які утворюють послідовність
Наслідком розглянутих теорем є інтегральна теорема Лапласа. У схемі незалежних повторних випробувань
де Аналогічними міркуваннями для цієї схеми легко дістати формулу:
38) Випадковим процесом Реалізацією випадкового процесу називається детермінована функція Кілька реалізацій певного випадкового процесу зображено на рис. 4.1. Нехай переріз цього процесу при даному t є неперервною випадковою величиною. Тоді випадковий процес Очевидно, що щільність імовірності Випадковий процес Таких перерізів нескінченно багато, але для задання випадкового процесу вдається обмежитись порівняльно невеликою кількістю перерізів. Випадковий процес має порядок п, якщо він повністю визначається щільністю спільного розподілу Випадковий процес може бути заданий числовими характеристиками. Математичним сподіванням випадкового процесу Дисперсією випадкового процесу Середнім квадратичним відхиленням Математичне сподівання випадкового процесу характеризує середню траєкторію всіх можливих його реалізацій, а його дисперсія або середнє квадратичне відхилення — розкид реалізацій відносно середньої траєкторії
Предмет курсу. Класифікація подій,класичне означення ймовірності випадкової події,статистичне означення ймовірності;елементи комбінаторики;аксіоми теорії ймовірностей та їх наслідки. Випробування — реальний або мислений експеримент (виконуваний за певної незмінної сукупності умов), результати якого піддаються спостереженню. Подія — результат випробування. Якщо в результаті випробування деяка подія неодмінно відбудеться, то вона називається достовірною і позначається літерою U. Подія, яка в даному випробуванні не може відбутись, називається неможливою і позначається літерою V. Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. Випадкові події позначаються літерами A, B, C, D, … Класичною імовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій, що утворюють простір елементарних подій W: P(A)= m /n. Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: W(A)= m /n. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин обчислюється за формулою: Pn = n! Розміщенням із n елементів по m (0 Комбінаціями з n елементів по m (0 Система подій називається алгеброю подій, якщо: 1. 2. із того, що Числова функція P, що визначена на системі подій Q, називається ймовірністю, якщо: 1. Q є алгеброю подій; 2. для будь-якого A Ì Q існує P(A)³0; 3. P(W)= 1; 4. якщо А і В є несумісними (АÇВ)=Æ, то P(AÈB)=P(A)+P(B); 5. для будь-якої спадної послідовності
Q,
Трійка (Q,W,R), де Q є алгеброю подій і Р задовольняє аксіоми 1-5, називається простором імовірностей. Наслідки аксіом: 1. якщо випадкові події 2. якщо випадкові події 3. формула додавання для n сумісних 4. якщо випадкова подія А сприяє появі В(АÌВ), то P(A)£P(B)
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.186.95 (0.009 с.) |

 m
m  = n! /(n-m)!
= n! /(n-m)! = n! / m!(n-m)!
= n! / m!(n-m)!
 ,
,  випливає, що:
випливає, що:  ,
,  ,
, 
 подій із Q, такої, що
подій із Q, такої, що випливає рівність
випливає рівність є несумісними попарно, то
є несумісними попарно, то 
 B) / P(B), P(B)
B) / P(B), P(B) 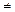 0. Властивості умовної ймовірності:
0. Властивості умовної ймовірності: (i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою:
(i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою:
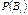 — імовірність події
— імовірність події 
 — умовні ймовірності настання події А.
— умовні ймовірності настання події А. Відомі ймовірності подій
Відомі ймовірності подій 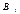 та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез
та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез  Для цього застосовують формулу Баєса:
Для цього застосовують формулу Баєса:
 з імовірностями
з імовірностями  Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Розподіл Пуассона розглядається як статистична модель для кількості альфа-частинок, що їх випромінює радіоактивне джерело за певний проміжок часу; кількості викликів, які надходять на телефонну станцію за певний період доби; кількості вимог щодо виплати страхових сум за рік; кількості дефектів на однакових пробах речовини і т. ін. Розподіл застосовується в задачах статистичного контролю якості, у теорії надійності, теорії масового обслуговування. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. Для цього розподілу складено таблиці щодо різних значень
Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Розподіл Пуассона розглядається як статистична модель для кількості альфа-частинок, що їх випромінює радіоактивне джерело за певний проміжок часу; кількості викликів, які надходять на телефонну станцію за певний період доби; кількості вимог щодо виплати страхових сум за рік; кількості дефектів на однакових пробах речовини і т. ін. Розподіл застосовується в задачах статистичного контролю якості, у теорії надійності, теорії масового обслуговування. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. Для цього розподілу складено таблиці щодо різних значень  (0,1 – 20). У таблицях для відповідних значень а наведено ймовірності
(0,1 – 20). У таблицях для відповідних значень а наведено ймовірності 
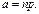


 m = 0,1,2, …, n. Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з імовірністю р. Частота настання події А має біноміальний закон розподілу. Числові характеристики розподілу:
m = 0,1,2, …, n. Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з імовірністю р. Частота настання події А має біноміальний закон розподілу. Числові характеристики розподілу:



 Параметри
Параметри  , які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини. Нормальний закон розподілу широко застосовується в математичній статистиці. Для обчислення ймовірності потрапляння випадкової величини, розподіленої нормально, на проміжок використовується функція Лапласа:
, які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини. Нормальний закон розподілу широко застосовується в математичній статистиці. Для обчислення ймовірності потрапляння випадкової величини, розподіленої нормально, на проміжок використовується функція Лапласа:


 послідовність незалежних випадкових величин,які задовольняють умовам:
послідовність незалежних випадкових величин,які задовольняють умовам: незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії
незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії  , то до послідовності (1) можна застосувати закон великих чисел. Це означає що середне арифметичне достатньо великої кількості незалежних випадкових величин дуже мало відрізняється від середнього арифметичного їхніх математичних сподівань,взятого за абсолютним значенням.
, то до послідовності (1) можна застосувати закон великих чисел. Це означає що середне арифметичне достатньо великої кількості незалежних випадкових величин дуже мало відрізняється від середнього арифметичного їхніх математичних сподівань,взятого за абсолютним значенням.
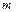 — частота події А у даних випробуваннях. Таким чином при необмеженому збільшенні числа незалежних випробувань за схемою Бернулі відносна частота дуже мало відрізняється від ймовірності.
— частота події А у даних випробуваннях. Таким чином при необмеженому збільшенні числа незалежних випробувань за схемою Бернулі відносна частота дуже мало відрізняється від ймовірності. розглянемо:
розглянемо:

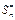 є нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.
є нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.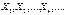 , існують моменти третього порядку і виконується умова
, існують моменти третього порядку і виконується умова то для
то для  виконується співвідношен-
виконується співвідношен-
 Це випливає з того, що частоту події можна подати як суму n випадкових величин — частот настання події в окремих випробуваннях. При достатньо великих значеннях n закон розподілу цієї суми близький до нормального.
Це випливає з того, що частоту події можна подати як суму n випадкових величин — частот настання події в окремих випробуваннях. При достатньо великих значеннях n закон розподілу цієї суми близький до нормального. де m — частота події А у n випробуваннях.
де m — частота події А у n випробуваннях. називається процес, значення якого за будь-якого значення аргументу t є випадковою величиною.
називається процес, значення якого за будь-якого значення аргументу t є випадковою величиною.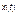 , на яку перетворюється випадковий процес
, на яку перетворюється випадковий процес  внаслідок випробування, тобто його траєкторія.
внаслідок випробування, тобто його траєкторія. при даному t визначається щільністю ймовірності
при даному t визначається щільністю ймовірності 
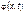 не є вичерпним заданням випадкового процесу
не є вичерпним заданням випадкового процесу  являє собою сукупність усіх перерізів за всіх можливих значень t, тому для його задання необхідно розглядати багатовимірну випадкову величину
являє собою сукупність усіх перерізів за всіх можливих значень t, тому для його задання необхідно розглядати багатовимірну випадкову величину  утворену з усіх перерізів цього процесу.
утворену з усіх перерізів цього процесу. п довільних перерізів процесу, тобто щільністю п -вимірної випадкової величини
п довільних перерізів процесу, тобто щільністю п -вимірної випадкової величини  де
де  — переріз випадкового процесу
— переріз випадкового процесу 
 називається детермінована функція
називається детермінована функція  яка за будь-якого значення змінної t дорівнює математичному сподіванню відповідного перерізу випадкового процесу
яка за будь-якого значення змінної t дорівнює математичному сподіванню відповідного перерізу випадкового процесу  , тобто
, тобто 
 називається детермінована функція
називається детермінована функція  , яка за будь-якого значення змінної t дорівнює дисперсії відповідного перерізу випадкового процесу
, яка за будь-якого значення змінної t дорівнює дисперсії відповідного перерізу випадкового процесу  , тобто
, тобто 
 випадкового процесу
випадкового процесу 



