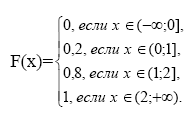Теорема 3. Формула полной вероятности

Пусть в результате опыта может появиться какое-либо из несовместных событий Н₁, Н₂,..., Н_n, образующих полную группу. Событие А может появиться только вместе с одним из этих событий. События Н₁, Н₂,..., Н_n называются гипотезами. Тогда вероятность события A равна P(A)= P(H_i)P(A/H_i).

Эта формула носит название формулы полной вероятности.

Пример 8. На стройку поступают блоки с трех баз, причем 50% с первой базы, 30% со второй базы, остальные с третьей базы. Вероятность того, что блок c первой базы бракованный - 0,09; со второй - 0,1; с третьей - 0,08. Найти вероятность того, что взятый наудачу на стройке блок окажется бракованным.

Решение.

Рассмотрим гипотезы:

Н₁ -взятый наудачу блок поступил с первой базы,

Н₂ -взятый наудачу блок поступил со второй базы,

Н₃ -взятый наудачу блок поступил с третьей базы.

Тогда из условия Р(Н₁)=50/100=0,5; Р(Н₂)=30/100=0,3; Р(Н₃)=(100-50-30)/100 = 0,2.

Событие А -взятый наудачу на стройке блок окажется бракованным.

По условию Р(А/Н₁)=0,09; Р(А/Н₂)=0,1; Р(А/Н₃)=0,08.

Следовательно, по формуле полной вероятности

Р(А)=0,5·0,09+0,3·0,1+0,2·0,08=0,091.

Теорема 4. Формула Байеса (теорема гипотез)

Пусть в условиях предыдущей теоремы событие А наступило и мы нашли вероятность Р(А). Тогда вероятности гипотез в связи с появлением события А, т.е. найдем Р(Н_i/А), равны где i=1,2,...,n.

Пример 9. В предыдущем примере событие А наступило, т.е. взятый наудачу на стройке блок оказался бракованным. Определить вероятность того, что этот блок поступил со второй базы.

Решение.

.

Теорема 5. Формула Бернулли

Производится n независимых испытаний, в каждом из которых событие А наступает с постоянной вероятностью р. Вероятность того, что в этих n испытаниях событие А появится ровно m раз равно P_n(m)= .

Пример 10. Каждый из пяти независимо работающих элементов отказывает с вероятностью 0,4. Найти вероятность того, что откажут три элемента из пяти.

Решение.

Р₅(3)= =10·0,064·0,36 ≈ 0,23.

Случайные величины

Случайной величиной Х в данном опыте называется переменная величина, которая в результате испытания примет одно из своих возможных значений, но какое именно до проведения опыта неизвестно.

Совокупность всех возможных значений случайной величины называется спектром. Спектр называется дискретным, если все возможные значения случайной величины образуют конечную или бесконечную последовательность, и называется непрерывным, если все значения случайной величины заполняют сплошь некоторый промежуток.

Например, Х - оценка на экзамене. Случайная величина Х имеет дискретный, т.к. ее возможные значения: 2; 3; 4; 5. Или Х - время безотказной работы двигателя. В этом случае случайная величина Х имеет непрерывный спектр, т.к. возможные значения Х заполняют сплошь некоторый промежуток времени [0;t], где t - момент отказа двигателя.

Функция распределения случайной величины

Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е. F(x)=P(X<x).

Из определения функции распределения следуют следующие свойства F(x):

1) область определения F(x) - интервал (- ∞;+∞),

2) 0 ≤ F(x) ≤1,

3) F(– ∞)=0, так как P(X< – ∞)=0,

4) F(+ ∞)=1, так как P(X<+∞)=1,

5) F(x) - неубывающая функция.

 

Законом распределения случайной величины Х называется любая ее вероятностная характеристика, из которой можно получить функцию распределения F(x).

Вероятность попадания случайной величины в промежуток и в точку

Если известна функция распределения F(x) случайной величины Х, то

P(α ≤ Х < β)=F(β)-F(α).

Дискретная случайная величина

Случайная величина Х называется дискретной, если ее спектр дискретный.

Законом распределения дискретной случайной величины Х является ряд распределения, т.е. перечисление всех возможных значений Х и их cоответствующих вероятностей:

р_i=P(X=x_i), где i=1;2;...;n;...

Многоугольником распределения назовем ломаную, соединяющую последовательно точки (х₁;р₁),(х₂;р₂),...,(х_n;р_n).

Пример 10. Среди шести элементов два изношенных. Составить ряд распределения случайной величины Х- числа изношенных элементов среди трех наудачу отобранных. Найти функцию распределения F(x) и построить ее график.

Решение.

Случайная величина Х может принимать значения: 0; 1; 2.

Условие нормировки: 0,2+0,6+0,2=1.

Найдем F(x).

Если x из (-∞;0], то F(x)=P(X<x)=0;

если x из (0;1], то F(x)=P(X<x)=P(X=0)=0,2;

если x из (1;2], то F(x)=P(X<x)=P(X=0)+P(X=1)=0,2+0,6=0,8;

если xиз (2;+ ∞), F(x)=P(X<x)=P(X=0)+P(X=1)+P(X=2)=0,2+0,6+0,2=1.

Следовательно,