
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое определение вероятности событияСодержание книги
Поиск на нашем сайте
Исход опыта называется благоприятным событию А, если в результате опыта событие А свершилось. Вероятностью события A назовем число Р(А)= Пример 4. Опыт- бросание игрального кубика. Событие А - выпадение числа очков, кратного 3. Пусть X – число очков, тогда все возможные исходы нашего опыта: (Х=1), (Х=2), (Х=3), (Х=4), (Х=5), (Х=6), равновозможны. Всего случаев n=6, благоприятных из них m=2, следовательно, P (A) = Элементы комбинаторики Имеется совокупность n объектов, назовем ее генеральной совокупностью. Из генеральной совокупности наудачу отбираем m объектов, эту отобранную совокупность назовем выборкой. Выборка может быть упорядоченной, если порядок объектов (элементов) играет роль, и может быть неупорядоченной, если порядок элементов роли не играет. Выборка может быть без повторений, если элементы повторяться не могут, и может быть с повторениями, если элементы в выборке повторяются. Например, телефонный номер 260-61-51 - упорядоченная выборка с повторениями из десяти цифр по семи. Упорядоченная выборка из n элементов по m называется размещением, неупорядоченная выборка из n элементов по m называется сочетанием. Число размещений и сочетаний c повторениями и без повторений из n элементов по m можно найти из следующей таблицы. Таблица 1
Пример 5. Два счета из десяти выполнены с ошибками. Найти вероятность того, что из четырех взятых на проверку счетов один счет окажется с ошибками. Решение. Воспользуемся классической формулой Р(А)=
Запомните: 0!=1. Основные теоремы Теорема 1. Теорема сложения вероятностей. Р(А1+А2+А3+...+Аn)=Р(А1)+Р(А2)+Р(А3)+...+Р(Аn) - Р(А1·А2) - Р(А1·А3) - … -Р(А1·Аn) - Р(А2·А3) -... - P(An-1·An)+P(А1·А2·A3)+P(А1·А2·A4)+...+P(Аn-2·Аn-1·An)+...+ +(-1)n-1 P(A1·A2·...·An). Следствие 1. Если события А1, А2,...,Аn несовместны, то Р(А1+А2+А3+...+Аn)=Р(А1)+Р(А2)+Р(А3)+...+Р(Аn). Следствие 2. Вероятность суммы двух любых событий равна сумме вероятностей этих событий без вероятности их произведения, то есть Р(А+В)=Р(А)+Р(В)–Р(А·В). Замечание. P(A) + P( Теорема 2. Теорема умножения вероятностей. Условной вероятностью Р(А / В) события А относительно события В назовем вероятность события А при условии, что событие В уже произошло. Теорема умножения. Р(А1·А2·А3·...·Аn)=Р(А1)·Р(А2/А1)·Р(А3/А1·А2) ·...·Р(Аn/А1·А2·А3·...·Аn-1). Правило (теорема) умножения для двух событий. Вероятность произведения двух любых событий равна произведению вероятности одного из них на условную вероятность другого относительно первого, то есть Р(А·В)=Р(А)·Р(В/А)=Р(В)·Р(А/В). Событие А называется независимым от события В, если условная вероятность события А относительно события Bравна безусловной вероятности события А, то есть Р(А/В)=Р(А). Нетрудно доказать, что если А не зависит от В, то и В не зависит от А. Следствие. Если события А и В независимы, то Р(А·В)=Р(А)·Р(В). Пример 6. Студент знает ответы на 20 из 25 вопросов. Какова вероятность того, что он ответит на два выбранных наудачу вопроса? Решение. Рассмотрим события: А- студент знает ответ на первый вопрос, В- студент знает ответ на второй вопрос. Найдем Р(А·В). Р(А·В) = Р(А)·Р(В/А) = Определение. Несколько событий называют независимыми (или независимыми в совокупности), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Следовательно, если А1, А2,...,Аn независимы, то справедливо правило умножения для независимых событий Р(А1·А2·А3·...·Аn)=P(A1)·P(A2)·P(A3)·...·P(An). Пример 7. Два студента выполняют независимо друг от друга задание. Вероятность того, что задание будет выполнено первым студентом 0,6; для второго студента эта вероятность равна 0,8. Найти вероятность того, что • оба студента выполнят задание; • только один из них выполнит задание; • хотя бы один из них выполнит задание. Решение. События: А - задание выполнит первый студент, В - задание выполнит второй студент. По условию Р(А) = 0,6; Р(В)=0,8; следовательно, Р( • Р(А·В) = /события А и В - независимые события / = Р(А)·Р(В) = 0,6·0,8 = 0,48. • Р(А· • P(A+B)=/ А и В-совместные события /= Р(А)+Р(В)-Р(А·В)=0,6+0,8– –0,48=0,92.
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.006 с.) |

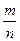 , где m – число благоприятных событию А исходов, n – число всех исходов в данном опыте.
, где m – число благоприятных событию А исходов, n – число всех исходов в данном опыте. =
=  .
.
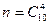 , так как имеем дело с неупорядоченными выборками без повторений, благоприятных из них
, так как имеем дело с неупорядоченными выборками без повторений, благоприятных из них  . Следовательно,
. Следовательно,
 ) = 1, откуда P(
) = 1, откуда P(
 ) = 1–0,8 = 0,2.
) = 1–0,8 = 0,2.


