
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закони збереження. Робота й енергіяСодержание книги
Поиск на нашем сайте
Основні формули
1. Закон збереження імпульсу
де N – кількість матеріальних точок (тіл) системи. 2. Робота, яка виконується постійною силою:
де α – кут між напрямками векторів сили F та переміщення ∆r. 3. Робота, яка виконується змінною силою:
де інтегрування здійснюється вздовж траєкторії, що позначається через L. 4. Середня потужність за інтервал часу ∆t
5. Миттєва потужність
6. Кінетична енергія матеріальної точки (тіла, що рухається поступально)
7. Потенціальна енергія тіла і сила, що діє на тіло в даній точці поля, пов’язані співвідношенням
де i, j, k – орти (одиничні вектори в напрямі осей x, y, z). Якщо поле сил має сферичну симетрію, одержимо такий зв’язок
8. Потенціальна енергія пружно-деформованого тіла
9. Потенціальна енергія гравітаційної взаємодії двох матеріальних точок (тіл) масами m1 і m2, що знаходяться на відстані r .
10. Потенціальна енергія тіла, що міститься в однорідному полі сили тяжіння,
де h (h<<R) – висота тіла над нульовим рівнем (рівнем, потенціальна енергія на якому умовно дорівнює нулю); R – радіус Землі. 11. У замкненій системі, в якій діють тільки консервативні сили, виконується закон збереження енергії
12. Швидкість руху куль після абсолютно непружного удару
13. Швидкості руху куль після абсолютно пружного удару
де m1 і m2 – маси куль; υ1 і υ2 – швидкості куль до взаємодії. Приклади розв’язання задач
Приклад 1. Куля масою 9 г, швидкість якої 600 м/с, попадає в дерев'яну стінку й застрягає в ній. Знайти середню силу удару й імпульс, отриманий стінкою, якщо час зіткнення 10 мс. Дано: m = 9 г = 9×10-3 кг
Dt = 10 мс = 10×10-3 с ___________________ <F > –?
Розв’язання. Відповідно до закону збереження імпульсу для довільної замкнутої системи тіл сумарний імпульс системи з часом не змінюється. Це означає, що
Куля до удару мала імпульс m
де Dpс – зміна імпульсу стінки; m За другим законом Ньютона для середніх значень маємо
<F>Dt = Dpc = m
Звідки середня сила удару кулі < Fc > дорівнює
< F> = Проведемо необхідні розрахунки:
<F> = При цьому сила < Fc> спрямована вздовж вектора початкової швидкості кулі, яку вона мала перед ударом.
Приклад 2. У кузов візка з піском загальною масою 40 кг, що рухається горизонтально зі швидкістю 5 м/с, попадає камінь масою 10 кг і застрягає в піску. Знайти швидкість візка після зіткнення з каменем, якщо камінь перед попаданням у візок летів зі швидкістю 5 м/с під кутом 60о до горизонту назустріч візку. Сили зовнішнього опору руху візка не враховувати. Дано: M = 40 кг
m = 10 кг a = 60о _______________ u –? Розв’язання. Оскільки силами опору в задачі можна знехтувати, то для такого руху система є замкнутою й для цієї системи тіл виконується закон збереження імпульсу (точніше, закон збереження горизонтальної складової імпульсу). Запишемо закон збереження імпульсу в напрямі руху візка
де M – маса візка з піском; m – маса каменя;
u – швидкість візка і каменя після непружної взаємодії.
Звідки одержуємо
Динаміка твердого тіла Основні формули 1. Основне рівняння динаміки обертального руху відносно нерухомої осі
де
Вектор моменту імпульсу тіла дорівнює
де r – радіус-вектор; mυ – імпульс тіла. У випадку постійного моменту інерції
де І – момент інерції тіла (міра інертності тіла при обертальному русі). 2. Момент імпульсу тіла, що обертається відносно осі
3. Момент сили F, що діє на тіло відносно осі обертання
де l – плече сили – найкоротша відстань від осі обертання до лінії дії сили. 4. Момент інерції матеріальної точки відносно нерухомої осі обертання
де m – маса точки; r – відстань від точки до осі обертання. Момент інерції довільного твердого тіла
де ri – відстань елемента маси ∆mi від осі обертання. Це ж співвідношення в інтегральній формі (для тіл правильної геометричної форми)
Якщо тіло однорідне, тобто його густина ρ однакова по всьому об’єму, то
де V – об’єм тіла.
Теорема Штейнера. Момент інерції твердого тіла або матеріальної точки відносно довільної осі обертання, але обов’язково паралельній до осі, що проходить через центр мас тіла, дорівнює
де І0 – момент інерції цього тіла відносно осі, що проходить через центр мас тіла; a – відстань між паралельними осями; m – маса тіла. 5. Закон збереження моменту імпульсу
Моменти інерції найпростіших тіл показані в таблиці 1:
Таблиця 1 Для двох взаємодіючих тіл закон збереження моменту імпульсу записується так:
де І1, І2 ,
Закон збереження моменту імпульсу для одного тіла із змінним моментом інерції
де І1і І2 – початковий і кінцевий моменти інерції;
6. Робота постійного моменту сили М, що діє на тіло, яке здійснює обертання
де 7. Миттєва потужність, яка розвивається при обертанні тіла,
8. Кінетична енергія тіла, яке здійснює обертальний рух
9. Кінетична енергія тіла, яке котиться без ковзання вздовж будь-якої площини
де
10. Зв’язок між роботою, яка виконується при обертанні тіла і зміною кінетичної енергії
11. Зв’язок між фізичними величинами і формулами, які характеризують поступальний і обертальний рух в найпростіших випадках, показаний в таблиці 2: Таблиця 2
Продовження таблиці 2 Приклади розв’язання задач
Приклад 1. Куля масою 1кг, рухаючись горизонтально, зіштовхується з нерухомою кулею масою 12 кг. Кулі абсолютно пружні, удар прямий, центральний. Яку частину своєї кінетичної енергії перша куля передала другій? Дано: m1 = 1 кг m2 = 12 кг
Удар пружний ____________ Е =
Розв’язання. При абсолютно пружному центральному зіткненні виконуються закони збереження імпульсу й енергії. Тому з урахуванням того, що друга куля до зіткнення була нерухома, одержуємо два рівняння
m1
де u1 й u2 – швидкості першої й другої куль після удару. При цьому із закону збереження імпульсу треба враховувати, що після удару перша й друга кулі рухаються уздовж прямої, по якій рухалася перша куля до удару. Частина енергії, передана першою кулею другій, визначається співвідношенням
де Кk1 – кінетична енергія першої кулі до удару; Кk2 – кінетична енергія другої кулі після удару. Розв’язавши систему (1), одержуємо
Підставивши u2 у формулу (2) і скоротивши на
Співвідношення (3) симетричне відносно мас куль m1 і m2, тому частина переданої енергії не зміниться, якщо маси куль поміняти місцями. Підставляючи у вираз (3) числові значення m1 і m2, одержимо
Приклад 2. З похилої площини висотою 1м і довжиною 10 м зсувається тіло масою 1 кг (рис.1). Знайти: а) кінетичну енергію тіла біля основи похилої площини; б) швидкість тіла біля основи похилої площини. Коефіцієнт тертя на всьому шляху вважати постійним і рівним 0,05.
h = 1 м l = 10 м m =1 кг f = 0,05 _________ E к –?
Роз’язання. Потенціальна енергія тіла при зсуванні з похилої площини переходить у кінетичну енергію й роботу проти сили тертя
mgh = Але h = l sin
Fтр.= f mg cosa. 1. Кінетичну енергію тіла знайдемо з (1)
Кk=
де sin Підставляючи чисельні значення, одержуємо Кk = 4,9 Дж.
2. Швидкість тіла одержимо з формули кінетичної енергії
Приклад 3. При вертикальному підніманні вантажу масою 4 кг на висоту 9 м постійною силою була виконана робота 80Дж. З яким прискоренням піднімали вантаж? Дано: m = 4 кг h = 2 м A = 80 Дж _________ a –? Розв’язання. Зовнішні сили виконують роботу, яка йде на збільшення потенціальної енергії вантажу й на надання йому прискорення
A = mgh + mah.
Звідси a =
Підставляючи чисельні значення, одержуємо
a =
Приклад 4. Сталева пружина під дією сили 300 Н видовжується на 2 см. Яку потенціальну енергією буде мати ця пружина при її видовженні на 10 см? Дано: F1 = 300 H x1 = 2 см = x2 = 10 см = 10-1 м __________________ En –?
Розв’язання. Потенціальна енергія розтягнутої пружини дорівнює Пn =
При цьому коефіцієнт жорсткості пружини можна визначити із закону Гука F = kx,
де F – величина зовнішньої сили. Звідси одержуємо
k = F/x = F1 / x1 . (2)
Якщо вираз (2) підставити в (1), одержуємо
Пn =
Підставляючи чисельні значення сили й деформацій, знаходимо
П n =
Дано: l = 1,5 м Рисунок 2 M = 10 кг m = 10 г = 10.10-3 кг
Розв’язання. Оскільки удар кулі в нижній кінець стрижня непружний, то після удару точки нижнього кінця стрижня і кулі будуть рухатися з однаковими швидкостями. Розглянемо детальніше явища, які відбуваються при ударі. Спочатку куля, вдарившись об стрижень, за достатньо малий проміжок часу приводить його в рух з кутовою швидкістю К =
де I – момент інерції стрижня відносно осі обертання. Потім стрижень повертається на кут У відхиленому положенні стрижень буде мати потенціальну енергію
П п =
Потенціальна енергія стрижня зростає за рахунок зменшення його початкової кінетичної енергії, а тому за законом збереження енергії вони рівні. Прирівнявши праві частини рівності (1) і (2), одержимо
Звідки
Момент інерції стрижня відносно осі обертання, яка проходить через кінець стрижня, можна знайти за теоремою Штейнера
I = I0 + M
Значення моменту інерції підставимо в (3), одержимо
cos
Щоб з виразу (4) знайти У початковий момент часу кутова швидкість стрижня w0 = 0, тому його момент імпульсу L01 = Iw0 = 0. Куля вдаряється в кінець стрижня й в міру заглиблення в стрижень, надає йому кутового прискорення та бере участь в обертанні стрижня навколо закріпленої осі. Момент імпульсу кулі перед початком удару L02 = m
де l – відстань точки влучення кулі від осі обертання стрижня. У кінцевий момент удару стрижень мав кутову швидкість L2 = m
Застосувавши закон збереження моменту імпульсу, можна записати
L01 + L02 = L1 + L2 або mυ0 l = Iw + ml2 звідки
Виконавши обчислення за формулою (5), а потім за формулою (4), знайдемо w = 0,99 рад/c; cosj = 0,95; j = 18,19o.
Приклад 6. Диск діаметром 20 см і масою 2 кг обертається навколо осі, яка проходить через його центр. Кут повороту диска змінюється з часом за законом j = А + Вt + Ct2, де C = -2 рад/c2. Визначити величину гальмівної сили, прикладеної до обода диска. Дано: D = 20 см = 0,2 м m = 2 кг j = А + Вt + Ct2 C = -2 рад/с2 ____________________ Fг –? Розв’язання. Плече гальмівної сили відоме. У цьому випадку воно дорівнює радіусу диска R. Тому гальмівну силу, прикладену до обода, можна знайти зі співвідношення Fг = M / R. Гальмівний момент М може бути розрахований з основного рівняння динаміки обертального руху М = І Для розрахунку цих двох величин є всі необхідні дані:
b =
Таким чином результуюча формула має вигляд
F =
Провівши необхідні розрахунки, одержимо
F = -2(1/2) рад/c2 × 2 кг × 0,2 м = - 0,4 Н.
Приклад 7. Вал у вигляді суцільного циліндра масою 10 кг насаджений на горизонтальну вісь. На вал намотаний шнур, до вільного кінця якого підвішена гиря масою 2 кг (рис.3). З яким прискоренням буде опускатися гиря, якщо її відпустити? Дано: m1 = 10 кг m2 = 2 кг __________ a –?
a =
де r – радіус вала. Кутове прискорення вала визначається з основного рівняння динаміки обертального руху тіла Рисунок 3
де M – обертальний момент, що діє на вал; I – момент інерції вала. Розглядаємо вал як однорідний циліндр (диск). Тоді його момент інерції відносно геометричної осі буде дорівнювати
I = Обертальний момент M, який діє на вал, дорівнює добутку сили натягу шнура T на радіус вала M = T r.
Силу натягу шнура знайдемо з таких міркувань. На гирю діють дві сили: сила тяжіння m2g, спрямована вниз, і сила T натягу шнура, спрямована вверх. Рівнодіюча цих сил викликає рівноприскорений рух гирі. За другим законом Ньютона
m2 g – T = m2 a, звідки T= m2 (g – a). Таким чином обертальний момент сил дорівнює
M = m2 (g – a) r.
Підставивши у формулу (2) отримані значення M і I, знайдемо кутове прискорення вала
Для визначення лінійного прискорення гирі підставимо цей вираз у формулу (1), одержимо
звідки
Гідростатика Основні формули 1. Витрата рідини в трубці, через яку вона тече: а) об’ємна витрата рідини QV = б) масова витрата рідини Qm = де S – площа перерізу трубки;
2. Рівняння нерозривності струменя
3. Рівняння Бернуллі для ідеальної нестисливої рідини в загальному випадку
де р1 і р2 – статичні тиски у двох умовно виділених перерізах трубки;
h1 і h2 – їх висота над деяким рівнем, прийнятим умовно за нульовий;
Якщо обидва перерізи розміщені на одній висоті, рівняння Бернуллі буде мати такий вигляд:
4. Швидкість витікання рідини з малого отвору у відкритій широкій посудині
де h – глибина, на якій міститься отвір відносно верхнього рівня рідини в посудині.
5. Формула Пуазейля. Об’єм рідини або газу, що протікає за час t через довгу трубку, дорівнює
де r– радіус трубки; l – її довжина;
6. Число Рейнольдса для потоку рідини в довгих трубках
і для руху кульки в рідині
де <
d – діаметр трубки або діаметр кульки.
Якщо Re<<Re кр –течія рідини ламінарна; Re>>Re кр –рух рідини переходить у турбулентний, де Re кр –критичне число Рейнольдса; (для руху кульки в рідині Re кр = 0,5; для потоку рідини Re кр = 2300). 7. Формула Стокса. Сила опору F, що діє з боку рідини на кульку, яка повільно рухається в ній, дорівнює
де r – радіус кульки; υ – швидкість руху кульки. Формула Стокса справедлива для швидкостей при яких Re<<1. Задачі 1. Прямолінійний рух матеріальної точки описується рівнянням Відповідь:
2. Рівняння руху двох матеріальних точок вздовж прямої лінії, мають вигляд: Відповідь: t = 1,1 c;
3. Рівняння руху точки вздовж прямої лінії має вигляд: Відповідь: F = 0,3 Н.
4. Визначити повне прискорення точки на ободі колеса радіусом 0,5 м, в момент часу t = 3с. Рівняння обертання колеса: Відповідь: а = 27,44 м/с2.
5. Точка рухається по колу радіусом 8 м. У деякий момент часу нормальне прискорення точки дорівнює 4м/c², вектор повного прискорення утворює у цей момент із вектором нормального прискорення кут 60o. Знайти швидкість Відповідь:
6. Матеріальна точка рухається прямолінійно. Рівняння руху має вигляд: Відповідь:
7. Швидкість частинки, яка рухається прямолінійно, змінюється за законом Відповідь: υе = 18м/с; х = 36.
8. Рівняння руху матеріальної точки вздовж прямої має вигляд: Відповідь: t = 0,2 c; x = 4,2 м; a = -10 м/с2.
9. Частинка рухається по прямій за законом Відповідь:
10. Частинка рухається прямолінійно з прискоренням а = 2В, де B = - 0,5 м/c². У момент часу t = 0 координата частинки x0 = 0, швидкість Відповідь: υ = -1 м/с; х = 1,5 м; S = 1,5м.
11. Точка рухалася впродовж t1=15c зі швидкістю υ1 = 5м/с, t2 = 10c зі швидкістю υ2 = 8м/с і t3 = 6 с зі швидкістю υ3 =20м/c. Яка середня шляхова швидкість Відповідь:
12. Рівняння прямолінійного руху має вигляд x = At + Вt2, де А = 4 м/с; В = -0,05м/с2. Побудувати графіки залежності координати й шляху від часу для даного руху.
13. Камінь падає з висоти h = 1200 м. Який шлях s пройде камінь за останню секунду свого падіння? Відповідь: s = 150 м.
14. Тіло зсувається з похилої площини, яка утворює кут 45o з горизонтом. Пройшовши шлях 36,4 см, тіло набуває швидкості 2 м/с. Чому дорівнює коефіцієнт тертя тіла об площину. Відповідь: μ = 0,2.
15. Тіло зсувається з похилої площини, яка утворює кут 45o з горизонтом. Залежність пройденого тілом шляху від часу задається рівнянням: Відповідь: μ = 0,51.
16. Похила площина довжиною 2м утворює кут 25o з площиною горизонту. Тіло, рухаючись рівноприскорено, зсувається з цієї площини за час 2 с. Визначити коефіцієнт тертя тіла об площину. Відповідь: μ = 0,35.
17. Схил крижаної гори направлений під кутом 30o до горизонту. Рухаючись по схилу знизу вверх, тіло в деякій точці має швидкість 10 м/с. Коефіцієнт тертя ковзання 0,1. Яку швидкість буде мати це тіло після його повернення в початкове положення? Відповідь: υ = 8,4 м/с.
18. У вагоні, що рухається горизонтально та прямолінійно з прискоренням a = 2 м/c2, висить на шнурі вантаж масою m = 0,2 кг. Знайти силу натягу шнура і кут відхилення шнура від вертикалі. Відповідь: Fн = 2,04 Н; φ = 11,3о.
19. Під час руху автомобіля масою 103 кг на нього діє сила тертя, яка дорівнює 0,1 його сили тяжіння. Яку силу тяги має розвивати двигун автомобіля, увипадках: а) рівномірного руху; б) руху з прискоренням а = 2,4 м/c²? Відповідь: F1 = 1000 H; F2 = 3400 H.
20. Тіло зсуваєтся з похилої площини, кут нахилу якої α = 30o. У деякій точці В швидкість тіла
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.203 (0.01 с.) |

 або
або  ,
, або
або 

 .
. або
або 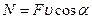 .
. або
або  .
.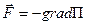 або
або  ,
,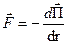 .
.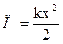 .
.

 .
. .
.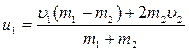 ,
,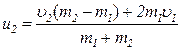 ,
, = 600 м/с
= 600 м/с pс –?
pс –?
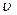 . Оскільки удар непружний, то цей імпульс буде повністю переданий стінці
. Оскільки удар непружний, то цей імпульс буде повністю переданий стінці .
. Н.
Н.
 – горизонтальна складова швидкості каменя;
– горизонтальна складова швидкості каменя;
 ,
, – результуючий момент всіх діючих сил;
– результуючий момент всіх діючих сил; – вектор моменту імпульсу тіла.
– вектор моменту імпульсу тіла. ,
,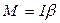 ,
, – кутове прискорення;
– кутове прискорення; .
. ,
, ,
,
 .
.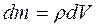 і
і  ,
,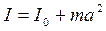 ,
, .
.



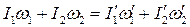 ,
,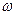 1,
1,  ,
,  ,
,  ,
,  – ті самі величини після взаємодії.
– ті самі величини після взаємодії.
 і
і 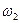 – початкова і кінцева кутові швидкості тіла.
– початкова і кінцева кутові швидкості тіла.
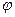 – кут повороту тіла.
– кут повороту тіла. .
.

 – кінетична енергія поступального руху тіла;
– кінетична енергія поступального руху тіла;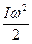 – кінетична енергія обертального руху тіла навколо осі, що проходить через центр інерції.
– кінетична енергія обертального руху тіла навколо осі, що проходить через центр інерції. .
.



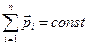



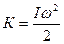
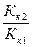 –?
–? , (1)
, (1)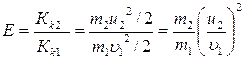 , (2)
, (2) .
.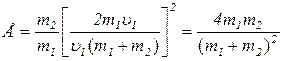 . (3)
. (3) .
. Дано:
Дано: . (1)
. (1) , де
, де  ,
, .
. .
. .
. м
м . (1)
. (1) .
. Дж.
Дж. Приклад 5. Стрижень довжиною 1,5 м і масою 10 кг може обертатися навколо нерухомої осі, яка проходить через верхній кінець стрижня (рис.2). У нижній кінець стрижня вдаряє куля масою 10 г, що летить у горизонтальному напрямі зі швидкістю 500 м/с, і застрягає в ньому. На який кут відхилиться стрижень після удару?
Приклад 5. Стрижень довжиною 1,5 м і масою 10 кг може обертатися навколо нерухомої осі, яка проходить через верхній кінець стрижня (рис.2). У нижній кінець стрижня вдаряє куля масою 10 г, що летить у горизонтальному напрямі зі швидкістю 500 м/с, і застрягає в ньому. На який кут відхилиться стрижень після удару?
 , (1)
, (1)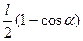 .
. . (2)
. (2)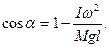 (3)
(3) =
=  M l2 +
M l2 +  M l2 =
M l2 =  M l2 .
M l2 . . (4)
. (4)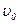 l,
l,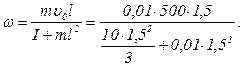 (5)
(5) = 2 C; I =
= 2 C; I =  – момент інерції диска.
– момент інерції диска. =
=  .
. Розв’язання. Лінійне прискорення a гирі дорівнює тангенціальному прискоренню точок вала, які лежать на його циліндричній поверхні, і пов'язане з кутовим прискоренням вала співвідношенням
Розв’язання. Лінійне прискорення a гирі дорівнює тангенціальному прискоренню точок вала, які лежать на його циліндричній поверхні, і пов'язане з кутовим прискоренням вала співвідношенням m1 r2.
m1 r2. .
. ,
,

 S,
S,
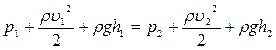 ,
, і
і  – швидкості рідини в цих перерізах;
– швидкості рідини в цих перерізах;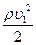 і
і  – динамічні тиски рідини в цих самих перерізах;
– динамічні тиски рідини в цих самих перерізах;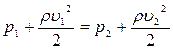 .
.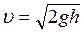 ,
, ,
, – різниця тисків на кінцях трубки;
– різниця тисків на кінцях трубки; – динамічна в’язкість (коефіцієнт внутрішнього тертя) рідини.
– динамічна в’язкість (коефіцієнт внутрішнього тертя) рідини. ,
, ,
, ,
, . Знайти екстремальне значення швидкості точки
. Знайти екстремальне значення швидкості точки  t1 = 5,3 c; t2 = 10,66 c.
t1 = 5,3 c; t2 = 10,66 c. , де B1 = 12 м/с,
, де B1 = 12 м/с,  і
і  , де B2 = 2 м/с,
, де B2 = 2 м/с,  . У який момент часу швидкості цих точок будуть однаковими? Чому дорівнюють швидкості і прискорення точок у цей момент часу?
. У який момент часу швидкості цих точок будуть однаковими? Чому дорівнюють швидкості і прискорення точок у цей момент часу? = 3,11 м/с; а1 = -8 м/с2;
= 3,11 м/с; а1 = -8 м/с2;  = 3,11 м/с; а2 =1 м/с2.
= 3,11 м/с; а2 =1 м/с2. , де А = 6 м/с і
, де А = 6 м/с і  . Визначити силу, яка діє на точку в момент часу t = 2 с. Маса точки m = 0,2 кг.
. Визначити силу, яка діє на точку в момент часу t = 2 с. Маса точки m = 0,2 кг.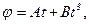 де А = 2 рад/c, B = 0,2 рад/c³.
де А = 2 рад/c, B = 0,2 рад/c³. = 5,65 м/с;
= 5,65 м/с;  .
. , де А = 3 м/с, B = 0,06 м/c³. Знайти швидкість і прискорення точки в моменти часу t1 = 0 і t2 = 3с. Яке середнє значення швидкості за перші 3 с?
, де А = 3 м/с, B = 0,06 м/c³. Знайти швидкість і прискорення точки в моменти часу t1 = 0 і t2 = 3с. Яке середнє значення швидкості за перші 3 с?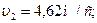 а = 1,08 м/с2;
а = 1,08 м/с2;  .
. , де А=12м/с і B=2м/c². Знайти: а) екстремальне значення швидкості частинки; б) координату х частинки для цього ж моменту часу, якщо в момент t = 0, х0 = 0.
, де А=12м/с і B=2м/c². Знайти: а) екстремальне значення швидкості частинки; б) координату х частинки для цього ж моменту часу, якщо в момент t = 0, х0 = 0. , де А = 4 м, В = 2 м/с, С = - 5 м/c². Знайти момент часу, в який швидкість точки
, де А = 4 м, В = 2 м/с, С = - 5 м/c². Знайти момент часу, в який швидкість точки 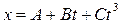 , де А = 3м, В = 2,5 м/с, С = 0,25 м/c³. Знайти середні значення швидкості і прискорення в інтервалі часу від t1 = 1c до t2 = 6c.
, де А = 3м, В = 2,5 м/с, С = 0,25 м/c³. Знайти середні значення швидкості і прискорення в інтервалі часу від t1 = 1c до t2 = 6c. ; аср . = 5,25 м/с2.
; аср . = 5,25 м/с2. точки?
точки? . Знайти коефіцієнт тертя тіла об площину.
. Знайти коефіцієнт тертя тіла об площину.


