
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коефіцієнт спрямованої дії. Максимальний КСД лінійних решіток визначається зі співвідношенняСодержание книги
Поиск на нашем сайте
де множник системи визначається формулою
у якій множник, що
.
Максимальний КСД рівно амплітудної лінійної решітки у режимі нормального випромінювання при числі елементів
де
В оптимальному режимі максимальний КСД лінійної решітки ще більше: При спадаючому до країв решітки амплітудному розподілі також існує оптимальний режим, причому оптимальне значення КСД більше, чим при рівно амплітудному. Це пояснюється тим, що спад амплітуди збудження до країв знижує рівень бічних пелюсток, отже, зі збільшенням
2.3. Вплив амплітудного розподілу на спрямовані властивості АР
При розподілі амплітуди збудливих струмів симетрично спадаючим до країв решітки спостерігається розширення головної пелюстки її ДС при одночаснім зниженні рівня бічних пелюсток і зменшенні КСД. Наприклад, у синфазної решітці при косинусоідному розподілі амплітуди струмів
спрямовані властивості визначаються множником системи
Ширину головного максимуму ДС «по нулях» і за рівнем половинної потужності в цьому випадку можна визначити зі співвідношень
Відношення При необхідності ще більшого зниження рівня бічних пелюсток можна застосувати більш різке спадання амплітуди збудливих струмів до країв ґрат. Є можливість вибрати такий закон розподілу амплітуд збудливих струмів, що бічних пелюсток взагалі не буде. Таку властивість мають решітки з біноміальним амплітудним розподілом і відстанню між елементами
Співвідношення амплітуд струмів в елементах ґ решіток визначається біноміальними коефіцієнтами, які, наприклад, можна взяти з таблиці 2.2 (трикутник Паскаля). Номер рядка в цій таблиці на одиницю менше числа випромінювачів у решітках. Кожну із цих решіток можна представити, що вона складається із двох решіток, що стоять у таблиці рядком вище, центри яких зрушені на відстань рівне кроку решітки. По теоремі перемножування характеристика спрямованості (ХН) розглянутих решіток є добуток ХН вищих решіток на ХН спрямованості системи двох випромінювачів, розташованих на відстані Застосовуючи теорему перемножування й для вищих решіток, доходимо висновку, що ХН будь-яких решіток з біноміальним розподілом амплітуд збудливих струмів і кроком Причому показник ступеня повинен бути на одиницю менше числа елементів у розглянутих решіток
А тому що ДС двоелементних решіток при кроці
2.4. Вплив фазового розподілу на спрямовані властивості АР
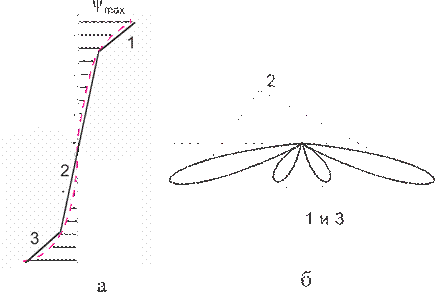
Відзначивши, що лінійний розподіл фази був розглянутий раніше, розглянемо ще два випадки функціональної залежності фази збудливих струмів в елементах лінійної эквидистантной решітки – квадратичне й кубічне розподілення. У цих випадках вивід аналітичних формул для характеристик спрямованості достатньо складний, а самі ці формули стають досить громіздкими. Тут можна навести лише елементарне трактування якісних змін, що відбуваються в решітках з нерівномірним фазовим розподілом. Квадратичний фазовий розподіл. Фаза збудливого струму пропорційна другому ступеню номера елемента в решітки, тобто фазовий множник (див. формулу (2.4)) має вигляд
де
У першому наближенні квадратичне розподілення фази (пунктирна лінія на рис. 1, а) можна апроксимувати лінійними розподілами на кожній половині решітки (суцільні лінії).
Рисунок 1 – Ілюстрація впливу квадратичного фазового розподілу
При цьому кожну половину решітки можна розглядати як решітку з лінійним розподіленням фази, головна пелюстка ДС якої відхиляється убік запізнювання фази (суцільні лінії на рис. 1, б). У міру збільшення Кубічний фазовий розподілення. У цьому випадку фаза збудливого струму пропорційна третьому ступеню номера елемента в решітці, тобто фазовий множник має вигляд
Кубічне розподілення фази (пунктирна лінія на рис. 2.8, а) приблизно можна апроксимувати трьома лінійними розподілами (суцільні лінії).
Рисунок 2 – Ілюстрація впливу кубічного фазового розподілу
При цьому кожну із трьох частин решітки можна розглядати як решітку з лінійним розподілом фази, головна пелюстка ДС якої відхиляється убік запізнювання фази (суцільні лінії на рис. 2.8, б). У міру збільшення
При косинусоидальному амплітудному розподіленні, як і в рівно амплітудної решітці, у міру зростання (при Таким чином, можна зробити висновки. Лінійні решітки з рівно амплітудним збудженням мають максимальне значення КСД у порівнянні з іншими типами розподілень у режимі нормального випромінювання. У режимі осьового випромінювання більший КСД мають решітки з нерівномірним амплітудним розподіленням, що спадає до країв. Однак використання останньої переваги пов'язане з певними труднощами, обумовленими зростанням "реактивності" антени. Квадратичні й кубічні фазові помилки приводять до зниження КНД. Ступінь зниження КСД залежить від значення помилки, а також від типу амплітудного розподілення. Якщо амплітудний розподіл спадає до країв решітки, то вплив фазових помилок зменшується, тому що знижується внесок у результуюче поле від найбільше расфазованних крайніх елементів.
Домашнє завдання
|
||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.193 (0.009 с.) |


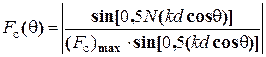 ,
, нормує, при
нормує, при  слід покласти рівним
слід покласти рівним  , а при
, а при  – визначити з виразу
– визначити з виразу .
.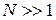 і кроці
і кроці  можна розрахувати по наступній наближеній формулі
можна розрахувати по наступній наближеній формулі
 - довжина решітки, а в режимі осьового випромінювання (при
- довжина решітки, а в режимі осьового випромінювання (при 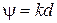 й кроці
й кроці  ) його можна розрахувати по формулі
) його можна розрахувати по формулі .
.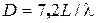 .
. оптимальний режим настає пізніше, тому що при цьому звуження головної пелюстки довше переважає над зростанням бічних пелюсток.
оптимальний режим настає пізніше, тому що при цьому звуження головної пелюстки довше переважає над зростанням бічних пелюсток. ,
,
 і
і 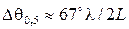 . При цьому відносний рівень першої бічної пелюстки
. При цьому відносний рівень першої бічної пелюстки  дБ.
дБ. може бути назване коефіцієнтом використання лінійної АР, який ураховує зниження КСД при нерівномірному амплітудному розподілі в порівнянні із синфазним рівно амплітудним збудженням. Так у синфазних решітках при косинусоідному амплітудному розподілі збудливих струмів
може бути назване коефіцієнтом використання лінійної АР, який ураховує зниження КСД при нерівномірному амплітудному розподілі в порівнянні із синфазним рівно амплітудним збудженням. Так у синфазних решітках при косинусоідному амплітудному розподілі збудливих струмів  . Відзначимо, що при спадаючому амплітудному розподілі також існує оптимальний режим осьового випромінювання. При цьому КСД виявляється ще більше, чим при рівно амплітудному.
. Відзначимо, що при спадаючому амплітудному розподілі також існує оптимальний режим осьового випромінювання. При цьому КСД виявляється ще більше, чим при рівно амплітудному. (крок може бути обраний рівним
(крок може бути обраний рівним  тільки для синфазних решіток).
тільки для синфазних решіток). , яка має тільки один головний максимум при будь-якім фазовім зсуві.
, яка має тільки один головний максимум при будь-якім фазовім зсуві.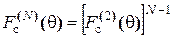 .
. ,
, – фазовий зсув струмів у крайніх елементах решітки, стосовно центрального елемента (максимальний фазовий зсув).
– фазовий зсув струмів у крайніх елементах решітки, стосовно центрального елемента (максимальний фазовий зсув).
 головна пелюстка сумарної ДС (пунктир) буде розширятися й при великих значеннях
головна пелюстка сумарної ДС (пунктир) буде розширятися й при великих значеннях  .
.
 головна пелюстка ДС буде усе більш відхилятися від нормалі до осі решітки, одночасно із цим відбувається збільшення РБП із боку, у який відбувається це відхилення.
головна пелюстка ДС буде усе більш відхилятися від нормалі до осі решітки, одночасно із цим відбувається збільшення РБП із боку, у який відбувається це відхилення. > kd одночасно відбуваються два процеси – звуження головної пелюстки й зростання відносного рівня бічних пелюсток. Однак через спадання амплітуди струмів до країв решітки фактор звуження головної пелюстки при зростанні (довше виявляє переважна дія. Для інших амплітудних розподілень, що більш різко спадають до країв, наприклад за законом "косинус у квадраті", ефект зростання КСД в оптимальному режимі виявляється ще сильніше.
> kd одночасно відбуваються два процеси – звуження головної пелюстки й зростання відносного рівня бічних пелюсток. Однак через спадання амплітуди струмів до країв решітки фактор звуження головної пелюстки при зростанні (довше виявляє переважна дія. Для інших амплітудних розподілень, що більш різко спадають до країв, наприклад за законом "косинус у квадраті", ефект зростання КСД в оптимальному режимі виявляється ще сильніше.


