
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент направленного действия. Максимальный кнд линейной решетки определяется из соотношенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где множитель системы определяется формулой
в которой нормирующий множитель
.
Максимальный КНД равноамплитудной линейной решетки в режиме нормального излучения при числе элементов
где
В оптимальном режиме максимальный КНД линейной решетки еще больше: При спадающем к краям решетки амплитудном распределении также существует оптимальный режим, причем оптимальное значение КНД больше, чем при равноамплитудном. Это объясняется тем, что спад амплитуды возбуждения к краям снижает уровень боковых лепестков, следовательно, с увеличением
2.3. Влияние амплитудного распределения на направленные свойства АР
При распределении амплитуды возбуждающих токов симметрично спадающем к краям решетки наблюдается расширение главного лепестка ее ДН при одновременном понижении уровня боковых лепестков и уменьшении КНД. Например, в синфазной решетке при косинусоидальном распределении амплитуды токов
направленные свойства определяются множителем системы
Ширину главного максимума ДН «по нулям» и по уровню половинной мощности в этом случае можно определить из соотношений
Отношение При необходимости еще большего снижения уровня боковых лепестков можно применить более резкое спадание амплитуды возбуждающих токов к краям решетки. Имеется возможность выбрать такой закон распределения амплитуд возбуждающих токов, что боковых лепестков вообще не будет. Таким свойством обладают решетки с биномиальным амплитудным распределением и расстоянием между элементами Соотношение амплитуд токов в элементах решетки определяется биномиальными коэффициентами, которые, например, можно взять из таблицы 2.2 (треугольник Паскаля). Номер строки в этой таблице на единицу меньше числа излучателей в решетке. Любую из этих решеток можно представить состоящей из двух решеток, стоящих в таблице строчкой выше, центры которых сдвинуты на расстояние равное шагу решетки. По теореме перемножения характеристика направленности (ХН) рассматриваемой решетки есть произведение ХН вышестоящей решетки на ХН направленности системы двух излучателей, расположенных на расстоянии Применяя терему перемножения и для вышестоящей решетки, приходим к выводу, что ХН любой решетки с биномиальным распределением амплитуд возбуждающих токов и шагом Причем показатель степени должен быть на единицу меньше числа элементов в рассматриваемой решетке
А так как ДН двухэлементной решетки при шаге
2.4. Влияние фазового распределения на направленные свойства АР
Отметив, что линейное распределения фазы было рассмотрено ранее, рассмотрим еще два случая функциональной зависимости фазы возбуждающих токов в элементах линейной эквидистантной решетки – квадратичное и кубическое распределения. В этих случаях вывод аналитических формул для характеристик направленности достаточно сложен, а сами эти формулы становятся весьма громоздкими. Здесь можно привести лишь элементарную трактовку качественных изменений происходящих в решетках с неравномерным фазовым распределением. Квадратичное фазовое распределение. Фаза возбуждающего тока пропорциональна второй степени номера элемента в решетке, т.е. фазовый множитель (см. формулу (2.4)) имеет вид
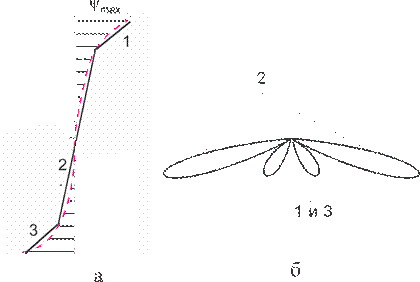
где В первом приближении квадратичное распределение фазы (пунктирная линия на рис. 1, а) можно аппроксимировать линейными распределениями на каждой половине решетки (сплошные линии).
Рисунок 1 - Иллюстрация влияния квадратичного фазового распределения
При этом каждую половину решетки можно рассматривать как решетку с линейным распределением фазы, главный лепесток ДН которой отклоняется в сторону запаздывания фазы (сплошные линии на рис. 1, б). По мере увеличения Кубическое фазовое распределение. В этом случае ф аза возбуждающего тока пропорциональна третьей степени номера элемента в решетке, т.е. фазовый множитель имеет вид
Кубическое распределение фазы (пунктирная линия на рис. 2.8,а) приближенно можно аппроксимировать тремя линейными распределениями (сплошные линии).
Рисунок 2 - Иллюстрация влияния кубичного фазового распределения
При этом каждую из трех частей решетки можно рассматривать как решетку с линейным распределением фазы, главный лепесток ДН которой отклоняется в сторону запаздывания фазы (сплошные линии на рис. 1, б). По мере увеличения При косинусоидальном амплитудном распределении, как и в равноамплитудных решётках, по мере роста y при y > kd одновременно происходят два процесса - сужение главного лепестка и возрастание относительного уровня боковых лепестков. Однако из-за спадания амплитуды токов к краям решётки фактор сужения главного лепестка при возрастании g дольше оказывает преобладающее действие. Для других амплитудных распределений, более резко спадающих к краям, например по закону "косинус в квадрате", эффект возрастания КНД в оптимальном режиме проявляется ещё сильнее. Таким образом, можно сделать выводы. Линейные решётки с равноамплитудным возбуждением имеют максимальное значение КНД по сравнению с другими типами распределений в режиме нормального излучения. В режиме осевого излучения больший КНД имеют решётки с неравномерным амплитудным распределением, спадающим к краям. Однако использование последнего преимущества связано с определёнными трудностями, обусловленными ростом "реактивности" антенны. Квадратичные и кубические фазовые ошибки приводят к снижению КНД. Степень снижения КНД зависит от значения ошибки, а также от типа амплитудного распределения. Если амплитудное распределение спадает к краям решётки, то влияние фазовых ошибок уменьшается, так как снижается вклад в результирующее поле от наиболее расфазированных крайних элементов.
3. Домашнее задание
|
||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 935; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.152.102 (0.008 с.) |


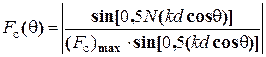 ,
, при
при  следует положить равным
следует положить равным 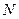 , а при
, а при  определить из выражения
определить из выражения
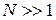 и шаге
и шаге  можно рассчитать по следующей приближенной формуле
можно рассчитать по следующей приближенной формуле
 - длина решетки, а в режиме осевого излучения (при
- длина решетки, а в режиме осевого излучения (при 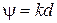 и шаге
и шаге  ) его можно рассчитать по формуле
) его можно рассчитать по формуле .
.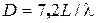 .
.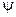 оптимальный режим наступает позже, так как при этом сужение главного лепестка дольше преобладает над ростом боковых лепестков.
оптимальный режим наступает позже, так как при этом сужение главного лепестка дольше преобладает над ростом боковых лепестков. ,
,
 и
и  . При этом относительный уровень первого бокового лепестка
. При этом относительный уровень первого бокового лепестка  дБ.
дБ. может быть названо коэффициентом использования линейной АР, который учитывает снижение КНД при неравномерном амплитудном распределении по сравнению с синфазным равноамплитудным возбуждением. Так в синфазных решетках при косинусоидальном амплитудном распределении возбуждающих токов
может быть названо коэффициентом использования линейной АР, который учитывает снижение КНД при неравномерном амплитудном распределении по сравнению с синфазным равноамплитудным возбуждением. Так в синфазных решетках при косинусоидальном амплитудном распределении возбуждающих токов  . Отметим, что при спадающем амплитудном распределении также существует оптимальный режим осевого излучения. При этом КНД оказывается еще больше, чем при равноамплитудном.
. Отметим, что при спадающем амплитудном распределении также существует оптимальный режим осевого излучения. При этом КНД оказывается еще больше, чем при равноамплитудном. (шаг может быть выбран равным
(шаг может быть выбран равным  только для синфазных решеток).
только для синфазных решеток). , которая имеет только один главный максимум при любом фазовом сдвиге.
, которая имеет только один главный максимум при любом фазовом сдвиге.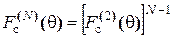 .
. ,
, – фазовый сдвиг токов в крайних элементах решетки, по отношению к центральному элементу (максимальный фазовый сдвиг).
– фазовый сдвиг токов в крайних элементах решетки, по отношению к центральному элементу (максимальный фазовый сдвиг).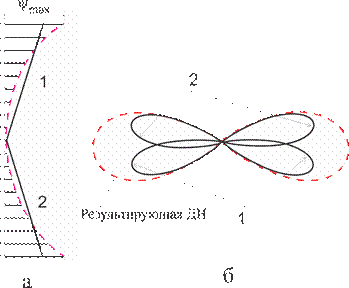
 главный лепесток суммарной ДН (пунктир) будет расширяться и при больших значениях
главный лепесток суммарной ДН (пунктир) будет расширяться и при больших значениях  .
.
 главный лепесток ДН будет все более отклоняться от нормали к оси решетки, одновременно с этим происходит увеличение УБЛ со стороны, в которую происходит это отклонение.
главный лепесток ДН будет все более отклоняться от нормали к оси решетки, одновременно с этим происходит увеличение УБЛ со стороны, в которую происходит это отклонение.


