
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидромеханический расчет спиральных камерСодержание книги Поиск на нашем сайте
Гидромеханический расчет спиральных камер производится с целью определения размеров входного и последующих сечений, обеспечивающих для заданных условий минимальные размеры камеры при наименьшем уровне гидравлических потерь. В основу расчета спиральных камер положены следующие условия: 1. В качестве расчетного принимается расход турбины Q, обеспечивающий получение ее номинальной мощности при расчетном напоре.
Во входном сечении спиральной камеры расчетный расход определяется равным
2. Вода подается равномерно по окружности направляющего аппарата, а следовательно, радиальная составляющая скорости υr имеет постоянное значение
3. Расход воды уменьшается по пути движения в спиральном канале в зависимости от φi
4. Окружная составляющая скорости υ и в любой точке спирального канала подчиняется закону
Расчет спиральных камер начинают с определения размеров входного сечения. Предварительные размеры входного сечения спиральных камер таврового сечения устанавливают в соответствии с рекомендациями пункта 7 (рис. 9). Площадь входного сечения определяют по зависимости
где υвх – средняя скорость потока во входном сечении спирального канала, которую выбирают по графику (рис. 10).
Рис. 10. График зависимости средней скорости спиральной камеры от напора турбины: 1 – в бетонной камере; 2 – в металлической камере
Значения углов охвата спирального канала φ 0 принимают по табл. 8. После установления размеров для выбранной формы входного сечения (рис. 8) выполняется проверка угла натекания потока δ сп по формуле:
где S 0 – интеграл входного сечения:
Интеграл входного сечения можно определить аналитическим путем по уравнению, полученному в результате интегрирования по участкам сечения
Представляя выражение (17) в формулу (16), определяют угол δ сп. Если он окажется меньше рекомендуемого (табл. 8), то его приводят в соответствие путем увеличения площади входного сечения. Из уравнений для δ сп и S 0 следует, что
Аналогичным образом можно получить значение Si и φi для любого сечения спирального канала. Для этого тавровое сечение разбивают на ряд участков, для которых становится известной зависимость b (r)(рис. 9). Для упрощения вычислений форму сечений назначают таким образом, чтобы вершины углов сечения лежали на прямых AB и CD (рис. 11). Зависимость между размером (Ri – ra) сечения и его высотами b 1 i и b 2 i задают в виде
где а 1 и а 2 – коэффициенты, а n1 и n 2 – показатели степени, принимаемые постоянными для данного спирального канала. Для спиральных каналов, развитых вверх n 1 = 2, n 2 = 0, а для сечений, развитых вниз n 1 = 0, n 2 = 2.
Рис. 11. К гидромеханическому расчету бетонной турбинной камеры
Для каналов с симметричной формой сечений принимают: · при угле φ 0 > 180° – n 1 = n 2 = 1, · при φ 0 ≤ 180° – n 1 = n 2 = 2. Коэффициенты а 1 и а 2 определяются по выбранным размерам входного сечения. Интеграл в любом сечении спирального канала На рис. 12 приведена конструкция металлической спиральной камеры круглого сечения.
Рис. 12. К гидромеханическому расчету металлической турбинной камеры
Для таких камер интеграл Si вычисляется по уравнению:
где ρi – радиус спирального канала:
rk – радиус сопряжения оболочки спирального канала:
Здесь Решение уравнений (18) и (21) является трудоемкой операцией, поэтому иногда используют приближенные решения, основанные на анализе результатов экспериментальных исследований и некоторых допущениях. Рассмотрим расчет бетонной спиральной камеры графоаналитическим способом на примере камеры симметричного очертания (рис. 13). Если определить площади в любом сечении спирального канала Si, то тогда можно найти значения Qi и φi, используя соотношения
Для этого входное сечение разбивают на ряд произвольных сечений с радиусом ri и строят зависимость
Рис. 13. К графоаналитическому расчету бетонной спиральной камеры
При приближенном аналитическом расчете металлической спиральной камеры круглого сечения значения интегралов S 0и Si определяют по зависимости
без учета площади
Рис. 14. Зависимости изменения угла охвата в спиральной камере
Подставляя значение интеграла (24) в выражение для φi, получим
где С – постоянная интегрированная, которую можно определить из (25) при известных значениях φ 0 (обычно принимают 345°) и радиусе входного сечения ρ 0. Радиус входного сечения определяют из выражения:
откуда
Среднюю скорость во входном сечении υс находят по графику (см. рис. 10). Из выражения (25) можно выразить радиус ρi в любой точке спирального канала
По вычисленным значениям φi и ρi ведется построение спиральной камеры в плане (см. рис. 12).
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.57 (0.006 с.) |

 , м3/с.
, м3/с.
 , м3/с.
, м3/с.
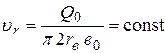 .
.
 , м3/с.
, м3/с.
 .
.
 , м2,
, м2,

 во входном сечении
во входном сечении ,
,
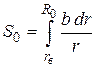 .
.
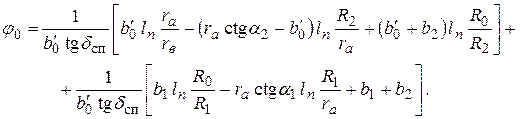
 ;
;  ,
,

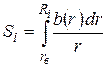 и соответствующее изменение угла охвата φi определяются по зависимостям (17) и (18) с учетом принятых соотношений для b 1 i и b 2 i (19).
и соответствующее изменение угла охвата φi определяются по зависимостям (17) и (18) с учетом принятых соотношений для b 1 i и b 2 i (19).
 ,
,
 ,
,
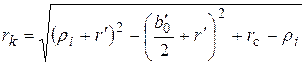 .
.
 = 0,12, а
= 0,12, а  = 0,695.
= 0,695. и
и  .
.
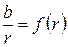 (см. рис. 13), на которой показаны графические значения интегралов S 0, S 1, S 2, … Sn. Зная значения Si, по условиям (23) определяют значения расходов и углов охвата в любой точке спирального канала и по ним строят зависимости Qi = f (ri) и φi = f (ri) (рис. 14). По значениям кривой φi = f (ri) строится очертание спирального канала в плане (см. рис. 11). При построении рекомендуется принимать значение радиусов ri для соответствующих значений Δ φ, равным 15 или 18°.
(см. рис. 13), на которой показаны графические значения интегралов S 0, S 1, S 2, … Sn. Зная значения Si, по условиям (23) определяют значения расходов и углов охвата в любой точке спирального канала и по ним строят зависимости Qi = f (ri) и φi = f (ri) (рис. 14). По значениям кривой φi = f (ri) строится очертание спирального канала в плане (см. рис. 11). При построении рекомендуется принимать значение радиусов ri для соответствующих значений Δ φ, равным 15 или 18°.

 , которая не оказывает существенного влияния на определение размеров входного сечения, а радиус rk принимается равным ra (см. рис. 12).
, которая не оказывает существенного влияния на определение размеров входного сечения, а радиус rk принимается равным ra (см. рис. 12).
 и расхода воды
и расхода воды 
 ,
,
 ,
,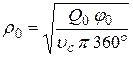 .
.
 .
.



