Некоторые понятия математики и логики, используемые в лингвистике

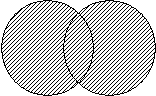
§ 179. В последние десятилетия в языкознании усилилось стремление к тому, чтобы лингвистические описания имели максимально точный, строгий и объективный характер. Описание языка обладает указанными признаками, если существуют определения лингвистических понятий, в принципе исключающие возможность различных толкований, а также имеются столь же точные, полные и недвусмысленные правила оперирования этими понятиями и приложения их к конкретному фактическому материалу (ср. § 197). Соблюдение изложенных требований делает весьма маловероятной ситуацию, при которой разные лингвисты, работающие с одним и тем же материалом, получают несовпадающие результаты[107]. Иначе говоря, результаты, полученные ученым, который использует точные методы исследования, должны быть воспроизводимыми: в рамках принятой системы понятий и методики они зависят лишь от объективных условий, т. е. от характера материала, поэтому другой исследователь на том же материале должен прийти к тем же выводам.

Вполне естественно, что в современных лингвистических работах, обнаруживающих стремление к точности анализа, нередко используются понятия и приемы логики и математики — наук, предоставляющих в распоряжение исследователя универсальный аппарат, который может быть использован для точного, свободного от субъективизма изучения и описания объектов самой разной природы. Не владея некоторыми элементарными понятиями из области логики и математики, иногда трудно следить за новейшей лингвистической литературой.

Необходимо сразу же сказать, впрочем, что использование специальных понятий математики в языкознании еще не есть математическое решение лингвистических проблем[108]. Гораздо чаще применение математических понятий реально служит скорее для уточнения, лучшего уяснения и более корректного изложения хода лингвистического анализа и его результатов, нежели для исследования, как такового. Думается, однако, что даже и эти возможности, которые дает нам математика, не следует игнорировать. /172//173/

Описанное выше положение во многом объясняется тем, что математика создавалась для изучения относительно простых объектов, которые более или менее легко поддаются формализации. Для анализа же столь сложных систем, как язык (или общество), «поведение» которых сравнительно слабо детерминировано, необходим, вероятно, особый математический и логический аппарат. Создание аппарата этого рода — дело будущего[109].

Особое место занимает в языкознании применение методов математической статистики. Без математико-статистической обработки данных невозможно обойтись в любом исследовании, оперирующем обширным фактическим материалом, который в принципе не может быть однородным и в котором можно обнаружить лишь статистические закономерности. Такая ситуация типична для экспериментальной фонетики, имеющей дело с результатами измерений параметров речи, для психолингвистических экспериментов, социолингвистических исследований и т. п. В этой небольшой книге практически невозможно изложить методику математико-статистической обработки опытных данных. Ниже мы остановимся лишь на разъяснении наиболее элементарных понятий неколичественной математики и логики.

§ 180. Одним из основных математических понятий является понятие множества. Определения множества не существует по той причине, что не существует более широкого понятия, частным случаем которого оно являлось бы. (Так, мы говорим: Млекопитающие — это животные, которые..., Звезды — это небесные тела, которые..., но для определения множества у нас нет слова, которое можно было бы употребить в соответствующем высказывании после слова это.)

Множество трактуют как совокупность предметов, объединенных каким-либо общим признаком, где слово «совокупность» просто синоним «множества», а не термин для более широкого понятия. Признак, объединяющий предметы в составе множества, может быть каким угодно. Например, все фонемы данного языка представляют собой некоторое множество, все словоформы данного текста образуют определенное множество, все тексты на русском языке составляют множество и т. д. и т. п.

Предметы, составляющие данное множество, называют его элементами. Запись A = {x, y,..., z} означает, что существует множество A, которое состоит из элементов x, y,...z.

Множество задают либо простым перечислением всех его элементов, либо путем указания на признак (или признаки) этих элементов. Например, мы можем задать множество A = {п, п’, б, б’, в, в’, м, м’, ф, ф’} путем перечисления всех его элементов (как это и сделано выше), но то же множество можно задать и путем указания на признак его элементов: A есть множество всех губных согласных русского языка.

Множество может состоять из одного-единственного элемента. Например, множество заднеязычных щелевых фонем русского языка состоит из одного элемента — фонемы х. /173//174/

Множество может быть пустым, т. е. не содержать ни одного элемента. Например, множество придыхательных русского языка является пустым[110]. Точно так же пустым является множество форм будущего времени совершенного вида 1‑го лица единственного числа глагола победить.

§ 180.1. Элементом множества может быть другое множество. В таких случаях говорят о подмножествах данного множества. Например, согласные составляют подмножество множества всех фонем, а губные согласные, в свою очередь, — подмножество множества согласных.

Принадлежность элемента множеству принято записывать так: xÎA (читается: «элемент x принадлежит множеству A»). Принадлежность подмножества записывается так: AÌM (читается: «множество A является подмножеством множества M»).

§ 180.2. У двух или более множеств могут быть общие элементы. Множество C, которое состоит из тех, и только тех элементов множеств A и B, которые принадлежат обоим этим множествам (A и B), называется произведением, или пересечением, множеств A и B. О множествах A и B в таком случае говорят, что они пересекаются. Например, множество всех губных согласных и множество всех звонких согласных русского языка пересекаются: в качестве их произведения выступает множество C = {б, б’, в, в’}.

Суммой, или объединением, множеств A и B называется множество C, которое включает все элементы A и все элементы B, и никакие другие элементы в множество C не входят. Например, сложение множества гласных и множества согласных дает сумму — множество всех фонем данного языка[111].

Множества A и B, в сумме дающие C, могут одновременно пересекаться. Чтобы учесть и этот случай, говорят, что C, т. е. объединение множеств A и B, есть множество всех тех элементов, каждый из которых принадлежит хотя бы одному из множеств-слагаемых, т. е. A или B. Например, если мы объединим множество A глухих согласных русского языка и множество B переднеязычных русских согласных, то часть элементов множества-суммы C будет принадлежать одновременно и A, и B (т, т’, ц, с, с’), часть же — только A (п, п’, ф, ф’, ш, ч, к, к’, х, х’) или только B (д, д’, з, з’, н, н’, л, л’).

§ 180.3. Разбиение множеств на непересекающиеся подмножества есть не что иное как классификация, которая занимает столь заметное место в лингвистике, во всяком случае при исследовательском подходе.

При классификации элементы относят к одному и тому же подмножеству на основании того, что все они обладают каким-либо определенным признаком, которого лишены элементы всех других подмножеств. Более точно это выглядит следующим образом. Обычно в качестве основания классификации выбирают признак, принимающий несколько значений, например, признак подъема для гласных, который принимает, допустим, три значения: верхний подъем, средний подъем, нижний подъем. Сколько значений принимает признак — столько подмножеств, или классов, выделяется. Например, а относится к гласным нижнего подъема, э, о — к гласным среднего подъема, и, у, ы — /174//175/ к гласным верхнего подъема. Получаем в результате три класса (подмножества) гласных.

§ 180.4. Элементы каждого класса (подмножества), полученные в результате классификации, находятся в отношении эквивалентности друг к другу. Иначе говоря, все они эквивалентны, или неразличимы с точки зрения данного признака. Элементы, находящиеся в отношении эквивалентности, характеризуются следующим: каждый элемент эквивалентен сам себе, что называется рефлексивностью; если элемент x эквивалентен элементу y, то элемент y эквивалентен элементу x, что называется симметричностью; если элемент x эквивалентен элементу y, а элемент y эквивалентен z, то элемент x эквивалентен z, что называется транзитивностью. Из наличия рефлексивности, симметричности и транзитивности соответственно следует эквивалентность.

Описанные условия очень важны. Необходимо также постоянно помнить, по какому признаку определяется отношение эквивалентности. Например, согласная /s/ эквивалентна согласной /z/ по месту и способу образования, а согласной /t/ — по месту образования и глухости. Разумеется, из этого не следует транзитивности с точки зрения всех признаков и не следует, что /s/, опять-таки с точки зрения всех признаков, эквивалентна /t/, хотя и можно, безусловно, сказать, что все три фонемы эквивалентны по месту образования (т. е. все они являются зубными, или переднеязычными).

§ 180.5. Кроме сложения и умножения множеств говорят также о вычитании множеств, результатом которого является их разность. Разностью множеств A и B называют множество C = A – B, в которое входят все элементы множества A, не принадлежащие B. В том случае, когда B является частью (подмножеством) множества A, разность A и B называют дополнением к множеству B в A.

Это важное для лингвистики понятие. Если рассматривать множество всех контекстов (окружений), в которых находится данная фонема или морфема, т. е. их полную дистрибуцию, то можно сказать, что подмножества контекстов, в которых встречаются несвободные варианты фонемы или морфемы, являются дополнениями друг к другу. Именно на этом и основано, по существу, понятие дополнительной дистрибуции.

§ 180.6. Сложение, умножение и вычитание множеств иллюстрируют обычно схемами, которые мы приводим ниже (см. рис. 1, 2, 3).

A C B	C   A B	C   A B
Рис. 1. A Ç B.	Рис. 2. A È B.	Рис. 1. A – B.

На рис. 1 показано пересечение множества A и B (символически A Ç B), их произведение — множество C (заштриховано). На рис. 2 показано сложение, или объединение множеств A и B (символически A È B), их сумма — множество C (заштриховано). На рис. 3 показано вычитание множеств A и B (символически A – B), их разность — множество C (заштриховано). /175//176/

§ 181. Операции, аналогичные умножению и сложению в теории множеств, в логике совершаются по отношению к высказываниям. Высказыванием называют некоторое предложение, которое может быть истинно или ложно; при этом не интересуются, во-первых, структурой высказывания, оно выступает как нечто цельное, и, во-вторых, тем, истинно или ложно данное высказывание в действительности. В логике занимаются только операциями над высказываниями, которые из истинных высказываний получают истинные, из истинных — ложные и т. д.

Над высказываниями можно осуществлять следующие операции:

1) отрицание: если высказывание X истинно, то его отрицание X–(«не-Х») ложно, и наоборот; X–по отношению к высказыванию X аналогично дополнению A — B по отношению к множеству B в A при отрицании множеств;

2) конъюнкция — отношение «и», объединение двух высказываний (аналогичное пересечению множеств): если высказывания X и Y одновременно истинны, то истинна и их конъюнкция X Ù Y («X и Y»).

3) дизъюнкция — отношение «или» («X или Y»): высказывание X Ú Y истинно, если хотя бы одно из высказываний истинно (эта операция аналогична сложению множеств); дизъюнкция может быть строгой (сильной) и слабой: первый тип представлен тогда, когда имеется в виду исключающее «или», т. е. «или X, или Y, но не оба одновременно», второй тип соответствует включающему «или» («и/или»), т. е. «или X, или Y, или оба одновременно»;

4) импликация — отношение «если..., то...»: высказывание X → Y истинно всегда, кроме того случая, когда X истинно, а Y ложно;

5) материальная эквивалентность — отношение «если, и только если»: сложное высказывание X →← Y ложно только тогда, когда X истинно, а Y ложно, или наоборот.

Все указанные операции также играют важнейшую роль в лингвистическом описании. Так, на операции отрицания построены все классификации, в основании которых лежат привативные оппозиции (см. § 47). Например, глухие представляют собой не что иное, как не-звонкие, т. е. результат применения операции отрицания к «звонкости».

На операции конъюнкции, по существу, основаны синтагматические связи, а не операции дизъюнкции — парадигматические.

Проиллюстрируем применение понятий строгой и слабой дизъюнкции. Возьмем высказывание X Ú Y, где X представляет собой высказывание «фонемы дифференцируют означающие морфем», а Y — «фонемы дифференцируют означающие слов». При строгой дизъюнкции высказывание X Ú Y окажется ложным, так как невозможно, чтобы фонемы дифференцировали, скажем, два слова, не дифференцируя одновременно хотя бы часть морфем, входящих в эти слова. При слабой дизъюнкции, однако, то же высказывание окажется истинным, но оно будет оставаться таковым и тогда, когда X ложно, а Y истинно, что с лингвистической точки зрения неприемлемо (слова опять-таки не могут дифференцироваться, если все их морфемы идентичны; разумеется, здесь в принципе не должна учитываться омонимия).

Из изложенного выше должно быть ясно, что традиционное высказывание «фонемы дифференцируют означающие морфем или слов» логически непра-/176//177/вомерно (это свойство фонем относится непосредственно только к морфемам).

Любопытно истолкование некоторых фактов грамматики изолирующих (также некоторых агглютинативных) языков в свете логических положений об импликации и материальной эквивалентности. Известно, что в языках типа русского употребление определенных показателей для выражения соответствующего грамматического значения обязательно: если нужно выразить, например, значение множественности, то употребляются окончания ‑ы, ‑и, ‑а и др.; если же употреблены указанные показатели, то словоформы передают значение множественности. Иначе говоря, употребление показателей и выражение значения множественности находятся в отношении материальной эквивалентности.

В отличие от этого в таких языках, как бирманский, тюркские и ряд других, употребление показателей множественного числа передает значение множественности, но из их неупотребления не следует значение единичности, например: бирм. са² оу⁴, турецк. китаб (без показателя множественного числа) могут передавать и значение «книга», и значение «книги». Иначе говоря, между употреблением показателей множественного числа и значением множественности существует отношение импликации: как было сказано выше, из ложности X в высказывании X → Y не следует ложность Y, т. е. из неупотребления показателя множественного числа не следует отсутствие значения множественности.

§ 182. В логике и математике очень важную роль играет понятие исчисления. Об исчислении говорят тогда, когда имеется точно определенный, количественно и качественно, алфавит — набор элементов, символов и имеются правила образования, или формационные правила, по которым из элементов данного алфавита можно построить формулы, или выражения. Правила должны перечислять абсолютно все возможные операции с символами, и только их. Выражения, полученные посредством применения правил, называются правильно построенными формулами (ппф), и они принимаются в качестве аксиом.

Примером могут служить цифры (алфавит) и арифметические операции с ними (формациоиные правила).

Обычно наряду с этим имеются также правила преобразования, или трансформационные правила, или правила вывода. По этим правилам, которые также носят точный и исчерпывающий характер, можно из аксиом построить новые выражения, допустимые в данной системе.

Такие системы называются формальными системами, исчислениями, или формализмами.

Если символы и выражения исчисления имеют определенную смысловую интерпретацию, то говорят, что исчисление является семантически интерпретированным. Интерпретация указывает, какие объекты, свойства, процессы описывает данное исчисление. Например, дифференциальные уравнения соответствующего вида описывают поведение механических или электрических колебательных систем, следовательно, этот фрагмент дифференциального исчисления семантически интерпретирован.

Исчисление, обладающее семантической интерпретацией, называют формальным (формализованным) языком. /177//178/

Легко видеть, что именно к идеям теории формальных систем восходят представления трансформационно-порождающей грамматики. Можно сказать, что в трансформационно-порождающей лингвистике грамматика предстает в виде формальной системы, алфавит которой — символы S, NP, VP, N, V и т. д., а формационные правила — правила подстановки. Ядерные предложения в общем аналогичны аксиомам (ппф), в качестве трансформационных правил выступают, естественно, трансформации. Каждое предложение мыслится как объект, который можно получить путем применения формационных и трансформационных правил к исходному алфавиту.

В полном согласии с представлениями, развиваемыми теорией исчислений, семантика в трансформационно-порождающей грамматике рассматривается как интерпретация символов и выражений формальной (синтаксической) системы, а понятие «язык» используется для обозначения совокупности правильно построенных предложений.

Предметный указатель*

Акт речевой (речевое действие) 5

Актант семантический см. партиципант

Актант синтаксический 100.1–100.2

Актуальное членение предложения 96.1

Алгоритм 152.2

Алломорф 55

Аллофон 41

Архифонема 48.6

Аффикс 59.2

Аффикс агглютинативный 59.2, 59.3

Аффикс флективный 59.2

Базис предложения 118.2

Валентность синтаксическая 95.1

Варьирование свободное 41.1, 55

Вершина синтаксического дерева см. дерева синтаксического вершина

Вида категория 82–82.5

Времена абсолютные 83.1–83.3

Времена относительные 83.1–83.3

Времени категория 83–84

Врожденность языковых структур 154–155

Гиперфонема 48.2 (прим.)

Глоттохронология 142–143

Голофраза 156.3

Грамматика зависимостей 101

Грамматика непосредственно составляющих 102–102.4, 105

Грамматика падежная (по Филлмору) 126

Грамматика Теньера 100–100.3

Грамматика членов предложения 96–97.99

Граммема 70

Данное (в актуальном членении предложения) см. тема (в актуальном членении предложения)

Двойное членение в языке 18, 19

Дерева синтаксического вершина 98

Дерева синтаксического ветви 98

Дерева синтаксического узлы 98

Дерево синтаксическое 98

Деривация 68.3, 108

Деривация в синтаксисе 108

Детерминанта 149

Деятельности мотив 164.1, 166.1–166.2

Деятельности уровень ведущий 164.1

Деятельности уровень фоновый 164.1

Деятельность 164.1

Деятельность речевая см. речевая деятельность

Диатеза 136

Дизъюнкция 181

Дистрибуция 41.1

Дистрибуция дополнительная в морфологии 55

Дистрибуция дополнительная в фонологии 41.1

Дополнение в логике 180.5

Дополнение как член предложения 97, 100.3

Единица решения при восприятии 172, 173

Залога категория 85–87

Знак 14

Знак абстрактный 16

Знак конкретный 16

Знака денотат 16

Знака десигнат см. знака означаемое

Знака десигнатор см. знака означающее

Знака означаемое 14

Знака означающее 14

Знака референт см. знака денотат

Знаков прагматика 15

Знаков синтактика 15

Значение (в отличие от смысла) 166.3

Значение второстепенное 74.4

Значение грамматическое 57–57.3

Значение инвариантное 74–74.4

Значение лексическое 57–57.3

Значение общее см. значение инвариантное

Значение основное 74.4

Избыточность речи 175, 177, 178

Импликация 181 /179//180/

Имя (в грамматике) 78

Имя (в семантике) 78

Инициаль 50

Интериоризация 166.8

Интонация 51.2

Исчисление 182

Категория классифицирующая 69, 81

Категория лексико-грамматическая см. категория классифицирующая

Категория морфологическая 69, 82–93

Категория общая 70

Категория семантическая 28

Категория формообразующая 69, 71, 73

Категория частная 70

Классификации признаки 75–78, 180.3

Классификация 180.3

Классификация слов 53 (прим.), 76–80, 133

Компетенция (по Хомскому) 114

Компонент грамматики семантический 118

Компонент грамматики синтаксический 118

Компонент грамматики фонологический 118

Конверсия 68.3

Конструкция номинативная 146.3

Конструкция синтаксическая 95

Конструкция эргативная 146.3

Контраст слоговой 174

Конъюнкция 181

Корень 58

Корреляты дифференциальных признаков фонемы 44, 44.1, 46

Корреляты лексические 134

Лексика 57–57.3

Лексикон см. словарь

Лексема 68

Лингвистика дескриптивная 39, 112

Множество 180

Модели аналитические 32

Модели восприятия речи см. модели аналитические

Модели исследовательские 33, 35, 37

Модели нейролингвистические 34

Модели порождающие 32

Модели порождения речи см. модели порождающие

Модели психолингвистические 34, 152.2–152.3

Модели речевой деятельности 32

Модели собственно лингвистические 34

Моделирование в лингвистике 32, 36–38

Модель 30, 31

Модус (по Филлмору) 126

Мора 146.1 (прим. 1)

Морф 55

Морфема 54

Морфема грамматическая см. морфема служебная

Морфема знаменательная 57–58

Морфема лексическая см. морфема знаменательная

Морфема полуслужебная 58

Морфема служебная 57–58

Морфемы вариант см. алломорф

Морфемы основной вариант 56

Морфонология 56

Мотивация (в речевой деятельности) см. деятельности мотив

Нейролингвистика 6

Нейтрализация 48.6, 71

Новое (при актуальном членении предложения) см. рема

Нулевой показатель 72.3

Образ результата 164.4, 166.6, 176

Обстоятельство 100.3

Объект 130

Оппозиции маркированный член 47

Оппозиции немаркированный член 47

Оппозиция 47

Оппозиция в морфологии 69

Оппозиция в фонологии 47

Оппозиция привативная 47, 48.3

Оппозиция пропорциональная 47

Определение 95.2, 100.3

Падеж 88

Падеж глубинный 126

Падежа адвербиальное употребление 92

Падежа дифференциальные признаки 93

Падежа категория 88–92

Падежа синтаксическое употребление 92

Парадигма 69, 89–91

Парадигма синтаксическая 107

Парадигматические отношения 13, 69, 107

Параметры лексические 134.2–134.4

Партиципант 130

План выражения 21, 26

План содержания 21

Подклассы слов 80

Подлежащее 96–96.2, 100.3

Подсистема языка 9

Позиция сильная 48

Позиция слабая 48 /180//181/

Позиция фонологическая 48

Показатель непосредственно составляющих 117

Показатель непосредственно составляющих базовый 118.2

Показатель непосредственно составляющих обобщенный 119

Показатель трансформационный 118.3

Правило контекстно-свободное 123 (прим. 10)

Правило контекстно-связанное 123 (прим. 10)

Правило перифразирования 109

Правило подстановки 118.1

Правило фонологическое 123

Праформа 141

Праязык см. язык-основа

Предикат 126, 132.3

Предложение включающее 103

Предложение производное 113

Предложение членное 103 (прим.)

Предложение ядерное 113, 118.2

Предложения линейная структура 102.2

Пропозиционирование 166.4, 167

Пропозиция (по Филлмору) 126

Просодические средства в фонологии 51

Рема 96.1

Речевая деятельность 5, 32 (прим.)

Речь 5

Речь внутренняя 4.2, 166.8

Роль семантическая см. партиципант

Связь взаимоподчинительная 97

Связь подчинительная 97

Связь синтаксическая 95.1

Сегмент минимальный в фонологии 41

Сегментация в морфологии 54

Сегментация в фонологии 39–40

Семиотика 14

Сепира — Уорфа гипотеза 4.1

Синтагматические отношения 13

Синтаксическое описание (в трансформационно-порождающей грамматике) 117

Сема см. смысл элементарный

Сирконстант 100.1

Система 8–9

Система фонем 43

Система функциональная 8

Система языка 5–10

Ситуация (в семантике) 130

Словарь 119, 121, 162

Словарь идеографический 133

Словарь идеологический см. словарь идеографический

Словарь толковый 136

Слова выделение 60–67

Слова цельнооформленность 62

Слово аналитическое 64

Слово графическое 61

Слово производное 68.3

Слово синтетическое 64

Слово служебное 59.1

Слово фонетическое 61

Словообразование 53 (прим.), 68–68.4

Словосочетания раздельноформленность 62

Словоформа 68, 72

Смысл 32, 161, 168, 178

Смысл (в отличие от значения) 166.3

Смысл элементарный 132–133, 135

Составляющая см. грамматика непосредственно составляющих

Составляющая глагольная 118.2

Составляющая именная 118.2

Способа действия категория 82–82.5

Структура 11–13

Структура глубинная 116–117, 118.3, 119–120, 125, 129

Структура поверхностная 116–117

Структура семантическая 126, 130, 166.4

Структура синтаксическая 94–95

Субкомпонент базовый (в трансформационно-порождающей грамматике) 118.1

Субкомпонент трансформационный 118.1

Субъект 130

Супрасегментные средства в фонологии см. просодические средства в фонологии

Таксономические единицы в синтаксисе 95.2

Текст 5, 32

Тема (при актуальном членении предложения) 96.1

Типология квантитативная 146.2

Типология классификационная 145

Типология контенсивная 147

Типология морфологическая 144, 146.2

Типология синтаксическая 146.3

Типология фонологическая 146.1

Типология характерологическая 145

Тон см. языки тональные

Трансформация 113, 118.2

Трансформация обобщенная 118.2

Трансформация одинарная см. трансформация сингулярная

Трансформация сингулярная 118.2

Ударение 51.1

Универсалии 149

Употребление (по Хомскому) 114

Управление 97 /181//182/

Уровень морфем 23.2, 54–59.4

Уровень морфологический 27, 52–93

Уровень предложений 23.1

Уровень семантики 28, 161, 124–135

Уровень синтаксический 27, 94–110

Уровень слова 23.2, 60–81

Уровень фонологический 23, 23.2, 39–51

Уровни речевой деятельности 23–28, 165–169, 178

Уровни системы языка 23–28

Участник ситуации см. партиципант

Финаль 50

Фон см. сегмент минимальный в фонологии

Фонема 39, 42

Фонема в разных фонологических школах 41.2, 45, 48–49, 122

Фонема сильная 48.4

Фонема слабая 48.4

Фонемный ряд 48.4

Фонемы вариант см. аллофон

Фонемы признаки 43–46, 163

Фонемы признаки бинарные см. фонемы признаки двоичные

Фонемы признаки двоичные 44–44.3

Фонология дихотомическая 44–44.3

Фонология порождающая 121–123

Форма слова аналитическая 72.1

Форма слова синтетическая 72.1

Форма слова сложная см. форма слова аналитическая

Формообразование 68

Фузия 59.2

Функциональные единицы в синтаксисе 95.2

Функция коммуникативная языка 1–3

Функция лексическая 134

Функция отражательная языка 2, 3

Функция синтаксическая 95.2

Цепочка базовая 118.2

Цепочка терминальная 102

Части речи 75–79

Чередование фонетическое живое (автоматическое) 41.2

Чередование фонетическое историческое 41.2

Члены предложения 96–97, 100.4

Эвристика 152.2, 156.2–156.3, 169, 172, 178

Эквивалентность 180.4

Эквивалентность материальная 181

Язык (в отличие от речи) 5, 6

Язык-основа 137

Язык-эталон 150

Язык в психолингвистическом смысле 6, 7

Язык в узколингвистическом смысле 6

Язык и мышление 2–4

Языки агглютинативные 144

Языки аналитические 144

Языки инкорпорирующие 144

Языки морные 146.1

Языки моросчитающие 146.1

Языки силлабные 146.1

Языки слоговые 49–50, 146.1

Языки слогосчитающие 146.-

Языки полисинтетические см. языки инкорпорирующие

Языки тональные 51.1

Языки флективные 144 /182//183/

 

Содержание

Предисловие. 3

Язык как важнейшее средство общения и как непосредственная действительность мысли. 5

Язык, речь, речевая деятельность. 10

Соотношение категорий языка, речи и речевой деятельности. 10

Языковая система. Структура языка. 12

Язык как система знаков. 16

Двойное членение в языке. План выражения и план содержания. 18

Уровни языка и речевой деятельности. 20

Основные модели лингвистического описания. 26

Фонология. 31

Морфология. 49

Предмет морфологии. 49

Уровень морфем. 50

Уровень слов. 57

Критерии выделения слова. 57

Словообразование и формообразование. 62

Формообразующие и классифицирующие категории. Части речи. Подклассы слов. 65

Важнейшие морфологические категории. 73

Синтаксис. 86

Структура предложения. 86

Парадигматические отношения в синтаксисе. 98

Трансформационно-порождающая грамматика. 101

Основные принципы генеративного синтаксиса. 101

Словарь и фонология в порождающей грамматике. 110

Семантика. 114

Порождающая семантика. 114

Семантика синтаксиса и семантика словаря. 118

Генетическое изучение языков. 126

Типологическое изучение языков. 130

О психолингвистике. 139

Вводные замечания. 139

Усвоение языка. Структура языка. 141

Порождение речи. 149

Восприятие речи. 156

Приложение. Некоторые понятия математики и логики, используемые в лингвистике 166

Предметный указатель. 172

 

 

 

Вадим Борисович Касевич

 

Элементы
общей
лингвистики

 

Утверждено к печати
Восточным факультетом
Ленинградского государственного
университета

 

Редактор Е. К. Борисова

Младший редактор Н. И. Платонова

Художник М. М. Мержеевский

Художественный редактор И. Р. Бескин

Технический редактор З. С. Теплякова

 

Корректор М. З. Шафранская

 

Сдано в набор 25/II 1977 г.

Подписано к печати 15/VII 1977 г.

А-02905. Формат 60×90¹/₁₆. Бум. № 1

Печ. л. 11,5. Уч.‑изд. л. 11,99

Тираж 6300 экз. Изд. № 4074. Зак. № 125

Цена 80 коп.

 

Главная редакция восточной литературы

издательства «Наука»

Москва К‑45, ул. Жданова, 12/1

 

3‑я типография издательства «Наука»

Москва Б‑143, Открытое шоссе, 28

 

[1] Термин «грамматика» употреблен здесь в самом широком смысле — как синоним описания языка.

[2] «Язык есть практическое,...действительное сознание», — пишут К. Маркс и Ф. Энгельс в «Немецкой идеологии» (Сочинения. Изд. 2, т. 3, с. 29).

[3] Недавно К. Г. Крушельницкая показала, что принятый в нашей литературе перевод высказывания К. Маркса относительно сущности языка не вполне точен: в действительности Маркс утверждает, что «непосредственной действительностью мысли является язык». Это существенно меняет дело, ибо в таком случае формулировка Маркса не содержит определения основной функции языка, а указывает на форму существования мысли.

[4] К такому выводу склонялся в особенности Б. Уорф.

[5] Как можно видеть, коммуникативная функция и в этом плане выступает как первичная.

[6] Эта автономия подтверждается также теми случаями патологии, когда при крайне низком уровне интеллектуальных возможностей (врожденном слабоумии и т. п.) больные тем не менее в достаточной мере овладевают языком. Такие факты свидетельствуют, что способность к овладению языком в общем не зависит от умственных способностей, как таковых.

[7] Подробнее о внутренней речи см. § 166.8.

[8] Как говорят, шахматные фигуры могут быть сделаны из чего угодно, при этом король останется королем, а пешка пешкой, т. е. отношения сохраняются. Однако шахматы не могут быть из воды или газа.

[9] Некоторых оговорок требуют знаки, относящиеся к единичным объектам, например Наполеон.

[10] Точнее, Ельмслев говорил в этом случае о «фигурах выражения», в отличие от «фигур содержания», семантических единиц (об этом см. § 28 и др.).

[11] Разумеется, членить на элементы значения нельзя, поскольку значение нематериально.

[12] Не случайно школьные грамматики определяют предложение как единицу, «выражающую законченную мысль».

[13] Строго говоря, frieden — двуморфемная единица (fried‑en), но от этого мы здесь можем отвлечься.

[14] О взаимодействии уровней речевой деятельности с психолингвистической точки зрения см. § 166 и сл.

[15] Компоненты плана содержания, имеющие соответствия в плане выражения и взятые как особые единицы, Л. Ельмслев называл «фигурами содержания».

[16] Если не учитывать естественных моделей, которые «стихийно» создаются мозгом, психикой человека при отображении внешней действительности (см. § 4.1).

[17] Функционирование такой действующей модели также можно назвать речевой деятельностью.

[18] В отличие от ряда лингвистов, мы понимаем под текстом не совокупность означающих, а определенным образом организованную последовательность двусторонних знаков (конкретных, когда рассматривается данный текст, а не абстрактная модель текста).

[19] Подробнее об этом см. главу «О психолингвистике».

[20] Два или более сегментов как бы «сплавляются» в фонетически единое целое.

[21] Для немецкого примера более адекватной была бы транскрипция [ae9].

[22] Малое надписное [ⁱ] указывает на особое качество гласного, вызванное наличием i‑образного перехода под влиянием соседнего мягкого.

[23] В русском языке возможно [g] перед [e], например, гэ — название буквы.

[24] Логически правильнее говорить не о признаке, например «смычная», а о признаке «смычность/щелинность» (или же, скажем, признаке «тип преграды»), который принимает два значения: «смычная» и «щелинная» («щелевая»).

[25] Можно, однако, заметить, что их выделение из класса согласных выглядит не вполне убедительно.

[26] Можно привести такую аналогию: признак деления на расы можно разбить на два двоичных «черный/нечерный» и «белый/небелый», однако сомнительно, чтобы это было оправдано с точки зрения антропологии.

[27] Вспомним, что в старых русских грамматиках твердые назывались «дебелыми», а, в соответствии с древнеиндийской традицией, ретрофлексные называются «церебральными», т. е. «мозговыми», «головными».

[28] Для тех случаев, когда невозможно перевести сегмент в сильную позицию ввиду отсутствия чередования, вводится понятие гиперфонемы — сложной единицы, объединяющей две или более фонемы, которые не противопоставлены в данной позиции и выбор между которыми невозможен. Например, первая гласная в слове стакан предатавляет гиперфонему /o/a/: это не /e/, и не /u/, которые могут встречаться в данной позиции, но нельзя определить, /o/ это или /a/, поскольку невозможно перевести данный гласный в сильную позицию.

[29] Само тождество морфемы в плане выражения определяется при этом живыми фонетическими чередованиями (см. § 41.2).

[30] Здесь следует отметить, что концепция Р. И. Аванесова положена в основу описания фонетики в последней академической «Грамматике современного русского литературного языка» (М., 1970).

[31] Для единообразия мы используем косые скобки не только для транскрибирования «сильных» фонем, но также при записи «слабых» фонем и фонемных рядов (Р. И. Аванесов для всех видов транскрипции использует квадратные скобки).

[32] Аналогичным образом конечный гласный в слове рóга — это слабая фонема /ъ/, не эквивалентная ударной /а/.

[33] Тождество морфемы, как и в учении Московской фон