
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опір зв’язних грунтів зсуву. Закон кулона для зв’язних грунтівСодержание книги
Поиск на нашем сайте Грунты в основании сооружений, а также при неодинаковых отметках их поверхности испытывают воздействие не только нормальных, но и касательных напряжений. Когда касательные напряжения по какой-либо поверхности в грунте достигают его предельного сопротивления, происходит сдвиг одной части массива грунта по другой.
В какой-то момент верхнее кольцо начинает двигаться по плоскости сдвига и возникает нормальное напряжение и касательное напряжение:
В связных грунтах:
Закон Кулона для глинистых грунтов: предельное сопротивление связного грунта сдвигу, есть функция первой степени от нормального давления состоящего из 2-х частей: прямопропорциональной давлению и независимой от него. Где
Ф – угол внутреннего трения грунта С – удельное сцепление грунта Для связных грунтов (пылевато-глинистые грунты) прямая σ – τ не проходит через начало координат, а отсекает отрезок c на оси τ, так как в связных грунтах, обладающих сцеплением между частицами, при отсутствии нормального давления (σ = 0) сопротивление грунта сдвигу больше нуля, что обусловливается силами сцепления. Таким образом, сопротивление связного грунта сдвигу складывается из сопротивления трения, пропорционального нормальному давлению, плюс сцепление, не зависящее от давления. 33. Графічна інтерпретація теорії Кулона-Мора. Кругові діаграми граничних напружень. Різні випадки діаграм граничних напружень при зсуві (для зв`язних та сипучих грунтів) Закон прочности Кулона – Мора устанавливает условия, при которых грунт деформируется без увеличения напряжений за счет изменения формы. При этом его объемная деформація предполагается неизменной.
(Известно, что угол трения aльфа между касательными и горизонтальными напряжениями может быть и меньшим угла фи и возрастание угла a, происходящее в процессе осадок грунта в точке М, иллюстрируется перемещением точки Е по дуге круга в точку А – см. рис. 1,б). 34. Определение показателей прочности грунта в приборе одноосного сжатия.
максимальное сдвигающее напряжение будет при sin2 35.Определение показателей прочности грунтов в стабилометре.
нормальные:
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 К грунту прикладывают 2 вида нагрузок: 1.нормальную сжимающую нагрузку N 2. сдвигающую касательную к поверхности среза нагрузку Т.
К грунту прикладывают 2 вида нагрузок: 1.нормальную сжимающую нагрузку N 2. сдвигающую касательную к поверхности среза нагрузку Т.

 y – угол внутреннего трения, с – величина, характеризующая силы сцепления, Р
y – угол внутреннего трения, с – величина, характеризующая силы сцепления, Р 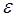 - давление связности.
- давление связности.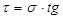 Ф+С
Ф+С -давление, которое срезает образец грунта
-давление, которое срезает образец грунта -нормальное давление на образец грунта
-нормальное давление на образец грунта


 Возможно лишь для тугопластичных и твердых глинистых грунтов.
Возможно лишь для тугопластичных и твердых глинистых грунтов. При испытании на простое одноосное сжатие образцов грунта увеличивают сжимающую нагрузку до тех пор, пока не произойдет разрушения образца или не возникнут прогрессивно возрастающие его деформации. Величину разрушающей нагрузки относят к еденице площади поперечного сечения образца, принимая распределение давлений равномерным, что,, однако, дает несколько заниженные значения сопротивлений, вследствии неучета неравномерности распределения давлений по краевым поверхностям образца. Если выделить по оси образца бесконечно малый элемент (рис. 2.19 а), то треугольная призмочка с углом
При испытании на простое одноосное сжатие образцов грунта увеличивают сжимающую нагрузку до тех пор, пока не произойдет разрушения образца или не возникнут прогрессивно возрастающие его деформации. Величину разрушающей нагрузки относят к еденице площади поперечного сечения образца, принимая распределение давлений равномерным, что,, однако, дает несколько заниженные значения сопротивлений, вследствии неучета неравномерности распределения давлений по краевым поверхностям образца. Если выделить по оси образца бесконечно малый элемент (рис. 2.19 а), то треугольная призмочка с углом  к оси давлений будет испытывать лишь напряжения показанные на рис 2.19б. Проектируя все силы на направление наклонной грани призмочки, получим
к оси давлений будет испытывать лишь напряжения показанные на рис 2.19б. Проектируя все силы на направление наклонной грани призмочки, получим 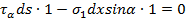
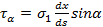 , или
, или 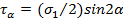 ;
;
 или, полагая
или, полагая  получим
получим  . Кривая придельных напряжений для рассматриваемого случая рис. 2.20
. Кривая придельных напряжений для рассматриваемого случая рис. 2.20 Результаты испытания дают возможность определить значение эффективных напряжений в момент разрушения образца. Кроме того по данным испытаний определяют: значения относительной продольной деформации:
Результаты испытания дают возможность определить значение эффективных напряжений в момент разрушения образца. Кроме того по данным испытаний определяют: значения относительной продольной деформации:  (
( –осадка для любой i-й ступени нагрузки; h – первоначальная высота образца грунта) и относительной обїемной деформации
–осадка для любой i-й ступени нагрузки; h – первоначальная высота образца грунта) и относительной обїемной деформации  изменение обїема образца, V – первоначальный объем). Результаты испытаний на трехосное сжатие дают возможность применить для оценки прочности грунтов, не только теорию прочности Мора, базирующуюся на законе Кулона, но и октаэдрическую теорию прочности, учитывающую пространственное напряженное состояние грунтов по октаэдрическим площадкам, равнонаклоненным к плоскостям главных напряжений. Нормальные и касательные напряжения на эти площадки, по решениям общей механики сплошных сред, будут равны:
изменение обїема образца, V – первоначальный объем). Результаты испытаний на трехосное сжатие дают возможность применить для оценки прочности грунтов, не только теорию прочности Мора, базирующуюся на законе Кулона, но и октаэдрическую теорию прочности, учитывающую пространственное напряженное состояние грунтов по октаэдрическим площадкам, равнонаклоненным к плоскостям главных напряжений. Нормальные и касательные напряжения на эти площадки, по решениям общей механики сплошных сред, будут равны: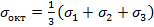 ; касательные:
; касательные: 



