
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование рациональных функцийСодержание книги
Поиск на нашем сайте
Частное от деления двух многочленов называют рациональной функцией или просто рациональной дробью, которая обычно обозначается R(x). Согласно определению R(x)= где Pm(x)-многочлен степени m, а Qn(x) - многочлен степени n. При этом дробь называется правильной, если m < n и неправильной, если m ≥ n. Всякую неправильную дробь можно представить в виде суммы многочлена (целой части дроби) и правильной рациональной дроби, разделив числитель на знаменатель, т.е. в виде R(x)= где Lr(x)- многочлен степени r = m-n (частное от деления), рk(х)- многочлен степени k<n (остаток от деления). Пример 1. Представить неправильную дробь R(x)= x3+5x-4 |x-1 x3-x 2 x2+x+6 x2+5x x2-x 6x-4 6x-6 Следовательно, R(x)= Всякую правильную дробь можно представить в виде суммы, так называемых, простейших дробей, указанных ниже четырёх видов: 1. 1. =
+ (N- Рассмотрим теперь разложение правильной рациональной дроби на простейшие. Вспомним, что, согласно теореме Гаусса, количество корней всякого многочлена равно показателю его наивысшей степени и многочлен можно, по теореме Безу, Qn(x)=Aoxn+A1xn-1+A2xn-2+…+An-1x+An=Ao(x-x1)(x-x2)…(x-xn), (3) где х1, х2, …, xn - корни многочлена среди которых могут быть кратные и комплексные, а каждому комплексному корню соответствует сопряжённый ему, тогда каждой паре комплексно спряжённых корней xj,, xj+1 в разложении (3) будет отвечать квадратный трёхчлен x2+pjx+qj c отрицательным дискриминантом. Если некоторый корень, например, xi повторяется k раз, то в разложение (3) войдёт множитель (x-xi)k, а если комплексный корень, например, xl повторяется r раз то в разложение (3) войдёт множитель (x2+plx+ql)r. Перепишем разложение (3) с учётом сказанного.
Qn(x)=Aoxn+A1xn-1+…+An-1x+An=Ao(x-x1)…(x-xi)k…(x2+pjx+qj) …(x2+plx+ql)r…(x-xn). (4) Если знаменатель правильной дроби (2) разложен на множители вида (4), то её можно представить в виде суммы простейших дробей, при этом каждому простому множителю вида (х-х1) соответствует простейшая дробь вида 1. Пример 2. Разложить правильную дробь Решение: Знаменатель дроби разложим на множители. x4+x3+x+1=x3(x+1)+x+1=(x+1)(x3+1)=(x+1)2(x2-x+1) и дробь представим в виде суммы простейших дробей с неопределёнными коэффициентами
3x2+4x-2=Ax2-Ax+A+Bx3+B+Cx3+2Cx2+Cx+Dx2+2Dx+D. Многочлены равны, следовательно, равны коэффициенты при одинаковых степенях. Приравняем их. При: х3 В+C=0, x2 A+2C+D=3, x -A+C+2D=4, x0 A+B+D = -2. Получили систему четырёх уравнений с четырьмя неизвестными. Из первого уравнения В=-С. Подставим в четвёртое получим систему трёх уравнений.
Решив систему получим: A=-1, B=-5/3, C=5/3 D=2/3, следовательно имеем искомое разложение.
Пример 3. Разложить правильную дробь Решение: Найдём корни знаменателя, разложим знаменатель на множители, приведём дроби к общему знаменателю и приравняем числители.
= Найдём неизвестные коэффициенты другим методом, который называется методом произвольных значений х. Этим методом удобно пользоваться, когда корни многочлена вещественные и различные. Дадим значения переменной х равные корням многочлена знаменателя и подставим их в последнее равенство получим: при х=0 A=2/3, при х=2 получаем В=-4, при х=3 – С=13/3. Искомое решение примет вид: В=-4 и при х=3 – С=13/3. Искомое разложение примет вид
На основании выше изложенного составим алгоритм нахождения интеграла от рациональной дроби. 1) Если дробь не правильная то надо выделить у неё целую часть, разделив числитель на знаменатель или другим методом и представить дробь в виде суммы многочлена и правильной дроби. 2) Разложить многочлен знаменателя на множители. 3) В соответствии с множителями знаменателя правильную дробь представить в виде суммы простейших дробей с неопределёнными коэффициентами. 4) Найти коэффициенты простейших дробей одним из выше указанных способов. 5) Проинтегрировать многочлен (целую часть дроби) и простейшие дроби. Пример 4. Найти
= = А(x+2)+B(x-1)(x+2)+C(x-1)2=2. Найдём коэффициенты методом произвольных значений х. Дадим значения переменной х равные -2; 1, получим: С=2/9, А=2/3, при х=0 получаем 2А-2В-С=2, 4/3-2В-2/9=2 отсюда В=4/9. Получаем:
Найдём окончательное выражение интеграла.
-
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.18.97 (0.01 с.) |

 , (1)
, (1) , (2)
, (2) в виде сум- мы многочлена и правильной дроби. Решение. Разделим числитель на знаменатель.
в виде сум- мы многочлена и правильной дроби. Решение. Разделим числитель на знаменатель. .
. ; 11.
; 11.  ; 111.
; 111.  ; 1V.
; 1V.  , где n=2,3,…, и квадратный трёхчлен x2+px+q имеет отрицательный дискриминант. Рас-смотрим интегрирование первых трёх видов простейших дробей.
, где n=2,3,…, и квадратный трёхчлен x2+px+q имеет отрицательный дискриминант. Рас-смотрим интегрирование первых трёх видов простейших дробей. =Aln(x-a)+C. 11.
=Aln(x-a)+C. 11. 
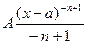 +C=
+C= +C. 111.
+C. 111.  dx. В данном интеграле в началевыделим в числителе производную знаменателя, т.е. выражение 2х+p, затем разделим числитель на знаменатель, почленно, получим два интеграла. В первом интеграле 2х+p подведём под знак интеграла, получим табличный интеграл 11. таблицы 2. Во втором интеграле выделим в знаменателе полный квадрат суммы вида x2+px+q=x2+px+
dx. В данном интеграле в началевыделим в числителе производную знаменателя, т.е. выражение 2х+p, затем разделим числитель на знаменатель, почленно, получим два интеграла. В первом интеграле 2х+p подведём под знак интеграла, получим табличный интеграл 11. таблицы 2. Во втором интеграле выделим в знаменателе полный квадрат суммы вида x2+px+q=x2+px+  -
-  )2+q-
)2+q-  , сделаем замену выражений, x+
, сделаем замену выражений, x+ 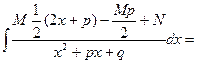

 +
+ )
)  =
=  + (N- -
+ (N- -  = =
= = 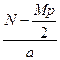 arctg
arctg  +C=
+C= 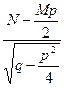 arctg
arctg  +C.
+C. разложить на множители следующим образом:
разложить на множители следующим образом: , множителю вида (x-xi)k - сумма простейших дробей вида
, множителю вида (x-xi)k - сумма простейших дробей вида  +
+ 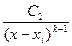 + …+
+ …+  , множителю x2+pjx+qj дробь вида
, множителю x2+pjx+qj дробь вида  ,а каждому множителю вида (x2+plx+ql)r –сумма дробей
,а каждому множителю вида (x2+plx+ql)r –сумма дробей 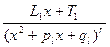 +
+  +…+
+…+  . Рассмотрим разложение правильной дроби на простейшие в примерах.
. Рассмотрим разложение правильной дроби на простейшие в примерах. на простейшие.
на простейшие. =
=  +
+  +
+  Коэффициенты A,B,C,D найдём методом сравнения коэффициентов при одинаковых степенях. Приведём дроби к общему знаменателю.
Коэффициенты A,B,C,D найдём методом сравнения коэффициентов при одинаковых степенях. Приведём дроби к общему знаменателю. . Дроби равны, знаме-натели равны, следовательно, равны и числители. Приравняем числители и одновременно раскроем скобки.
. Дроби равны, знаме-натели равны, следовательно, равны и числители. Приравняем числители и одновременно раскроем скобки.
 +
+  +
+  .
. на простейшие.
на простейшие. =
=  =
= . x2+4=A(x-2)(x-3)+Bx(x-3)+Cx(x-2).
. x2+4=A(x-2)(x-3)+Bx(x-3)+Cx(x-2). .
. . Решение. Под знаком интеграла дробь неправильная. Запишем отдельно дробь. В числителе выделим знаменатель и почленно разделим.
. Решение. Под знаком интеграла дробь неправильная. Запишем отдельно дробь. В числителе выделим знаменатель и почленно разделим. =
=  =1-
=1-  . Целая часть многочлена равна единице. Полученную правильную дробь разложим на простейшие.
. Целая часть многочлена равна единице. Полученную правильную дробь разложим на простейшие.  =
=  =
= 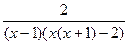 =
= =
=  =
=  =
=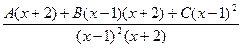 . Приравняем числители.
. Приравняем числители. =1-
=1-  .
. =x+
=x+  -
-  ln|x-1|-
ln|x-1|- ln|x+2|+C.
ln|x+2|+C.


