
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания для выполнения семестровой работыСодержание книги
Поиск на нашем сайте
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра высшей математики НЕОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ Методические указания для выполнения семестровой работы
Волгоград 2011
УДК
Рецензент
А.Е. Годенко
Издаётся по решению редакционно-издательского отдела Волгоградского государственного технического университета.
Неопределённые интегралы: Методические указания для выполнения семестровой работы / сост. В.И.Шушков, В.Н.Поляков.
Волгоград: ИУНЛ ВолгГТУ, 2011.-23с. В пособии представлены рекомендации по изучению темы «Неопределённый интеграл». Изложен в кратком виде теоретический материал, необходимый для нахождения интегралов. Показаны разные методы нахождения интегралов. Дано много решённых примеров нахождения интегралов от различных классов функций. Рассмотрены решения одних и тех же интегралов различными методами. Предназначено для студентов первого курса всех специальностей и всех форм обучения. ©Волгоградский государственный Технический университет 2011.
или подготовка к восприятию интегралов Прежде чем приступить к изучению интегрального исчисления, необходимо повторить дифференциальное исчисление, ибо действие интегрирования является обратным по отношению к операции дифференцирования, а обратные действия являются более сложными. Так, например, извлечение корня (обратное действие по отношению к возведению в степень) более сложное действие, чем возведение в степень, действия с обратными тригонометрическими функциями также являются более сложными, чем действия с тригонометрическими функциями и т.д. При интегрировании особо часто будем пользоваться понятием дифференциала функции, поэтому вспомним о том, что дифференциалом функции называется произведение производной функции на дифференциал аргумента, т.е. дифференциал функции y=f(x) определяется формулой dy=f′(x)dx (1) если у=f(x) сложная функция вида y=f(u(x)), то согласно свойству инвариантности дифференциала (1) можно записать в виде dy=f′(u)du (2) Вспомним дифференциалы основных элементарных функций:
Таблица 1 ТАБЛИЦА ДИФФЕРЕНЦИАЛОВ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНЦИЙ 1. d(um)=mum-1du. V1. d(ctgu)=- 11. d(lnu)= (11)*. d(log a u)= 111. d(sinu)=cosu du V111. d(arctgu)= 1V. d(cosu)=-sinudu (V111)*. d(arcctgu)= - V. d(tgu)= Но в интегральном исчислении чаще всего нам надо будет читать эти формулы справа налево. При этом будет искать такую функцию f(x), дифференциалом которой является выражение вида ψ(x)dx, т.е. чтобы соблюдалось равенство ψ(x)dx=df(x), а это уже действия обратные по отношению к нахождению дифференциала функции и они сложнее. Поэтому потренируемся выполнять такие действия на примерах. Пример 1. Найти такие функции, дифференциалы которых описываются следующими выражениями: а) x2dx; b) sin(2x)dx; c) sin(x)cos(x)dx; d) g) Решение: а) x2dx; замечаем, что по формуле (1) d(x3)=3x2dx, следовательно, x2dx= d( b) sin(2x)dx; подведём число 2 под знак дифференциала и, соответственно разделим на 2, получим sin(2x)dx= =- c) sin(x)cos(x)dx; решим этот пример различными способами. В начале представим произведение sin(x)cos(x) по формуле двойного угла для синуса - получим sin(x)cos(x)dx= ла cos(x) получим sin(x)cos(x)dx= sin(x)dsin(x)= =- d) e) f) Мы привели решение без пояснений оно на начальном этапе похоже на решение в предыдущем примере, лишь в конце воспользовались формулой 11. табл.1. g) =(-2(cosx)(sinx)+cosx)dx=(cosx-sin2x)dx, следовательно, в числителе стоит дифференциал знаменателя, тогда имеем h) =dln(5+3lnx). Здесь u=5+3lnx. t) Попробуйте самостоятельно ответить на вопрос дифференциалы, 1) 7) Правильность решения проверьте дифференцированием.
§2 Первообразная функция и неопределённый интеграл Потренировались немного, а теперь пeрейдём непосредственно к неопределённым интегралам. Во-первых, вспомним, что неопределённый интеграл от функции f(x) есть совокупность первообразных этой функции, а первообразной функции f(x) называется такая функция F(x) производная которой равна f(x), т.е. выполняется условие F′(x)= f(x). Это определение неопределённого интеграла. И ещё вспомним, что функция f(x) имеет множество первообразных, и все они отличаются друг от друга на постоянное слагаемое (теорема 1), поэтому в определении и фигурирует слово «совокупность». В справедливости теоремы мы уже убедились, решив пример 1с) на стр.5. Перейдём теперь к теоремам, которые непосредственно указывают на взаимную обратимость действий интегрирования и дифференцирования. Теорема 2. Интеграл от дифференциала функции F(x) равен дифференцируемой функции F(x) плюс произвольная постоянная. Или-в символической записи теорема записывается так:
Очень полезная теорема. С помощью этой теоремы можно находить некоторые интегралы методом подведения под знак дифференциала. Далее мы в этом убедимся на примерах. Теорема 3. Производная от интеграла по переменной интегрирования равна интегрируемой функции. В символической записи терема примет вид:
Эта теорема позволяет нам проверять правильность нахождения интегралов, т.е. нахождения первообразных. Осталось вспомнить свойства интегралов, которые определяются следующими двумя теоремами: Теорема 4. Интеграл от суммы функций равен сумме интегралов от слагаемых. Или в символах:
ТАБЛИЦА ИНТЕГРАЛОВ Таблица 2 1. 11. 111. 1V. V. V1. V11. (V11.)* V111. (V111.)* Здесь переменная u может быть независимой переменной или некоторой функцией от другой переменной, например, u=u(x). Формулы 1.-Х1V. непосредственно следуют после применения теоремы (2) к аналогичным номерам таблицы 1. При применении табличных интегралов иногда бывает полезной формула Метод замены переменной. Если в Пример 1. Найти Пример 2. Найти В некоторых интеграла лучше найти такую функцию t=t(x), чтобы под знаком интеграла было выражение Пример 3. Найти Успех при интегрировании методом замены переменной во многом зависит от того, насколько мы удачно выбрали функцию.
Интегрирование по частям. Если функции u=u(x) и v=v(x) имеют непрерывные производные, то справедлива формула
которая называется формулой интегрирования по частям. При этом в левом интеграле за u и v выбираются такие функции, чтобы в правой части получился интеграл, либо табличный, либо более простой, чем в левой части. С помощью этой формулы находятся, например, интегралы вида: 1. 11. 111. . Найти следующие интегралы: Пример 1. Найти В правой части получили интеграл опять вида 1., но степень многочлена уменьшилась. Применим к нему опять формулу интегрирования по частям полагая за u=2x+3 за dv=cos - =-2(x2+3x)cos +16cos Пример 2. Найти
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра высшей математики НЕОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ Методические указания для выполнения семестровой работы
Волгоград 2011
УДК
Рецензент
А.Е. Годенко
Издаётся по решению редакционно-издательского отдела Волгоградского государственного технического университета.
Неопределённые интегралы: Методические указания для выполнения семестровой работы / сост. В.И.Шушков, В.Н.Поляков.
Волгоград: ИУНЛ ВолгГТУ, 2011.-23с. В пособии представлены рекомендации по изучению темы «Неопределённый интеграл». Изложен в кратком виде теоретический материал, необходимый для нахождения интегралов. Показаны разные методы нахождения интегралов. Дано много решённых примеров нахождения интегралов от различных классов функций. Рассмотрены решения одних и тех же интегралов различными методами. Предназначено для студентов первого курса всех специальностей и всех форм обучения. ©Волгоградский государственный Технический университет 2011.
или подготовка к восприятию интегралов Прежде чем приступить к изучению интегрального исчисления, необходимо повторить дифференциальное исчисление, ибо действие интегрирования является обратным по отношению к операции дифференцирования, а обратные действия являются более сложными. Так, например, извлечение корня (обратное действие по отношению к возведению в степень) более сложное действие, чем возведение в степень, действия с обратными тригонометрическими функциями также являются более сложными, чем действия с тригонометрическими функциями и т.д. При интегрировании особо часто будем пользоваться понятием дифференциала функции, поэтому вспомним о том, что дифференциалом функции называется произведение производной функции на дифференциал аргумента, т.е. дифференциал функции y=f(x) определяется формулой dy=f′(x)dx (1) если у=f(x) сложная функция вида y=f(u(x)), то согласно свойству инвариантности дифференциала (1) можно записать в виде dy=f′(u)du (2) Вспомним дифференциалы основных элементарных функций:
Таблица 1 ТАБЛИЦА ДИФФЕРЕНЦИАЛОВ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНЦИЙ 1. d(um)=mum-1du. V1. d(ctgu)=- 11. d(lnu)= (11)*. d(log a u)= 111. d(sinu)=cosu du V111. d(arctgu)= 1V. d(cosu)=-sinudu (V111)*. d(arcctgu)= - V. d(tgu)= Но в интегральном исчислении чаще всего нам надо будет читать эти формулы справа налево. При этом будет искать такую функцию f(x), дифференциалом которой является выражение вида ψ(x)dx, т.е. чтобы соблюдалось равенство ψ(x)dx=df(x), а это уже действия обратные по отношению к нахождению дифференциала функции и они сложнее. Поэтому потренируемся выполнять такие действия на примерах. Пример 1. Найти такие функции, дифференциалы которых описываются следующими выражениями: а) x2dx; b) sin(2x)dx; c) sin(x)cos(x)dx; d) g) Решение: а) x2dx; замечаем, что по формуле (1) d(x3)=3x2dx, следовательно, x2dx= d( b) sin(2x)dx; подведём число 2 под знак дифференциала и, соответственно разделим на 2, получим sin(2x)dx= =- c) sin(x)cos(x)dx; решим этот пример различными способами. В начале представим произведение sin(x)cos(x) по формуле двойного угла для синуса - получим sin(x)cos(x)dx= ла cos(x) получим sin(x)cos(x)dx= sin(x)dsin(x)= =- d) e) f) Мы привели решение без пояснений оно на начальном этапе похоже на решение в предыдущем примере, лишь в конце воспользовались формулой 11. табл.1. g) =(-2(cosx)(sinx)+cosx)dx=(cosx-sin2x)dx, следовательно, в числителе стоит дифференциал знаменателя, тогда имеем h) =dln(5+3lnx). Здесь u=5+3lnx. t) Попробуйте самостоятельно ответить на вопрос дифференциалы, 1) 7) Правильность решения проверьте дифференцированием.
§2 Первообразная функция и неопределённый интеграл Потренировались немного, а теперь пeрейдём непосредственно к неопределённым интегралам. Во-первых, вспомним, что неопределённый интеграл от функции f(x) есть совокупность первообразных этой функции, а первообразной функции f(x) называется такая функция F(x) производная которой равна f(x), т.е. выполняется условие F′(x)= f(x). Это определение неопределённого интеграла. И ещё вспомним, что функция f(x) имеет множество первообразных, и все они отличаются друг от друга на постоянное слагаемое (теорема 1), поэтому в определении и фигурирует слово «совокупность». В справедливости теоремы мы уже убедились, решив пример 1с) на стр.5. Перейдём теперь к теоремам, которые непосредственно указывают на взаимную обратимость действий интегрирования и дифференцирования. Теорема 2. Интеграл от дифференциала функции F(x) равен дифференцируемой функции F(x) плюс произвольная постоянная. Или-в символической записи теорема записывается так:
Очень полезная теорема. С помощью этой теоремы можно находить некоторые интегралы методом подведения под знак дифференциала. Далее мы в этом убедимся на примерах. Теорема 3. Производная от интеграла по переменной интегрирования равна интегрируемой функции. В символической записи терема примет вид:
Эта теорема позволяет нам проверять правильность нахождения интегралов, т.е. нахождения первообразных. Осталось вспомнить свойства интегралов, которые определяются следующими двумя теоремами: Теорема 4. Интеграл от суммы функций равен сумме интегралов от слагаемых. Или в символах:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.119 (0.016 с.) |


 1X. d(еu)= еu du
1X. d(еu)= еu du . V11. d(arcsinu)=
. V11. d(arcsinu)=  X. d(shu)=chudu
X. d(shu)=chudu . (V11)*. d(arccosu)=-
. (V11)*. d(arccosu)=-  X1. d(chu)=shudu
X1. d(chu)=shudu X11. d(thu)=
X11. d(thu)= 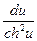
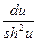
 1X. d(аu )= аu ln а du X1V.
1X. d(аu )= аu ln а du X1V. 
 ; e)
; e)  ; f)
; f)  ;
; ; h)
; h) 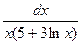 , t)
, t) 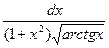 .
. x3);
x3); sin(2x)d(2x)=
sin(2x)d(2x)= dcos(2x). Т.е. мы пришли к предыдущему примеру. Подведём теперь под знак дифференциа-
dcos(2x). Т.е. мы пришли к предыдущему примеру. Подведём теперь под знак дифференциа-
 =-
=-  . Здесь мы воспользовались формулой X1V. табл. 1 при этом учли, что u=(1-x2).
. Здесь мы воспользовались формулой X1V. табл. 1 при этом учли, что u=(1-x2). =d(arcsinx), получим
=d(arcsinx), получим  =dln(arcsinx). В этом примере сработала формула X1. табл.1, где u=(arcsinx).
=dln(arcsinx). В этом примере сработала формула X1. табл.1, где u=(arcsinx). =(arcsin-2x)d(arcsinx)=-d(arcsinx)-1=-d
=(arcsin-2x)d(arcsinx)=-d(arcsinx)-1=-d  .
. =dln(cos2x+sinx). (u=cos2x+sinx, формула 11. табл.1).
=dln(cos2x+sinx). (u=cos2x+sinx, формула 11. табл.1). , следовательно,
, следовательно,  =
=  =
= =2
=2 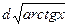 .
.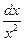 ; 2) tgxdx; 3) ctgxdx; 4)
; 2) tgxdx; 3) ctgxdx; 4)  ; 5) xsin(x2)dx; 6)
; 5) xsin(x2)dx; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  .
.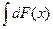 = F(x)+С. (3)
= F(x)+С. (3) . (4)
. (4) . (5)
. (5) , m# -1. 1X.
, m# -1. 1X.  .
. (1X.)*
(1X.)* 
 X.
X. 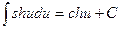




 Х111.
Х111. 
 = -arccosu+C X1V.
= -arccosu+C X1V. 
 XV.
XV. 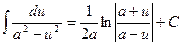
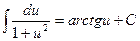 =- arcctgu+C XV1.
=- arcctgu+C XV1. 
 = -
= - 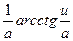 +C
+C . (7)
. (7) можно найти такую функцию x=x(t) и dx=
можно найти такую функцию x=x(t) и dx= 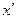 (t)dt, что после замены переменной
(t)dt, что после замены переменной  в правой части получаем более простой интеграл или табличный, то имеет смысл воспользоваться такой заменой.
в правой части получаем более простой интеграл или табличный, то имеет смысл воспользоваться такой заменой.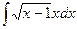 . Решение. Положим x=t2+1, тогда dx=2tdt, x-1=t2
. Решение. Положим x=t2+1, тогда dx=2tdt, x-1=t2  =t. Получаем
=t. Получаем  +С. Перейдём к старой переменной х. Имеем t=
+С. Перейдём к старой переменной х. Имеем t=  +С.
+С. . Решение. Пусть x=asint, тогда dx=acostdt,
. Решение. Пусть x=asint, тогда dx=acostdt,  =
=  . Эта подстановка позволяет нам освободиться от корня. Получаем
. Эта подстановка позволяет нам освободиться от корня. Получаем 
 =
=  Здесь мы воспользовались формулой понижения для косинуса: cos2t=
Здесь мы воспользовались формулой понижения для косинуса: cos2t=  , t=arcsin
, t=arcsin 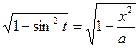 , sin2t=2
, sin2t=2  =2
=2 
 =
=  (arcsin
(arcsin  +
+ 
 )+C.
)+C. .
. . Решение. Возьмём функцию t=sinx, dt=cosxdx. Выполним замену переменной, получим
. Решение. Возьмём функцию t=sinx, dt=cosxdx. Выполним замену переменной, получим 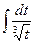 =
= 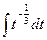 =
= 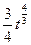 +С. Выполним обратную замену, получим
+С. Выполним обратную замену, получим 
 , (8)
, (8) emxdx,
emxdx, 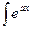 cos(bx)dx,
cos(bx)dx,  . Решение. Интеграл 1. вида, следовательно, u=x2+3x, dv=sin
. Решение. Интеграл 1. вида, следовательно, u=x2+3x, dv=sin  dx, тогда du=(2x+3)dx, v= -2 cos
dx, тогда du=(2x+3)dx, v= -2 cos  .
. ). К последнему интегралу применим формулы (6), (7) и 1. таблицы 2. Получим окончательный результат
). К последнему интегралу применим формулы (6), (7) и 1. таблицы 2. Получим окончательный результат  . Решение. Имеем интеграл вида 11., поэтому положим u=arcsinx, dv=xdx, тогда du=
. Решение. Имеем интеграл вида 11., поэтому положим u=arcsinx, dv=xdx, тогда du=  по формуле (8) по-лучим:
по формуле (8) по-лучим: 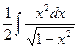 .(*) Найдём последний интеграл отдельно. К нему можно также применить формулу интегрирования по частям, хотя он и не похож ни на один из трёх видов интегралов, указанных выше. Положим за u=x, а за dv=
.(*) Найдём последний интеграл отдельно. К нему можно также применить формулу интегрирования по частям, хотя он и не похож ни на один из трёх видов интегралов, указанных выше. Положим за u=x, а за dv=  =-
=- 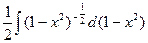 =-
=-  =x
=x  dx. Под знаком интеграла, в правой части равенства, умножим и разделим на
dx. Под знаком интеграла, в правой части равенства, умножим и разделим на 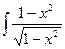 dx= -x
dx= -x  -
-  . Решение. Интеграл вида 111.. Полагая u=e3x, dv=cos
. Решение. Интеграл вида 111.. Полагая u=e3x, dv=cos 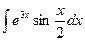 . В правой части интеграл того же вида. Положим опять u=e3x, за dv=sin
. В правой части интеграл того же вида. Положим опять u=e3x, за dv=sin  e3x(sin
e3x(sin 


