
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Барометрична формула. Розподіл Максвелла- Больцмана.Содержание книги
Поиск на нашем сайте
Рівняння, що дає змогу визначити зміну тиску повітря з висотою, називають барометричною формулою.
Це рівняння називають барометричною формулою. Вона досить точно справджується для невеликих висот (кілька кілометрів). Барометрична формула показує, що з висотою тиск експоненціально спадає і тим швидше, чим більша молярна маса газу або нижча температура. З формули також видно, що зменшення тиску залежить від прискорення вільного падіння. Розпо́діл Ма́ксвелла-Бо́льцмана визначає ймовірність того, що частинка ідеального газу перебуває в стані з певною енергією. Ймовірність того, що частинка перебуває в стані з енергією εk згідно з розподілом Больцмана визначається формулою:
де μ – хімічний потенціал, T — температура, kB — стала Больцмана.
де N — число частинок. Розподіл Больцмана справедливий тільки в тих випадках, коли температурах.
Середня довжина вільного пробігу молекул Число зіткнень. Ефективний діаметр. Довжиною вільного пробігу молекули називається відстань, яку молекула пролітає за час руху від одного стикання до іншого. Ці відстані можуть бути різними. Тому в кінетичній теорії вводять поняття середньої довжини вільного пробігу молекул. Величина є характеристикою усієї сукупності молекул газу за певних значень тиску та температури. Із збільшенням температури збільшується середня довжина вільного пробігу молекул. Це відбувається за рахунок зміни величини , яку можна розглядати як деякий ефективний діаметр молекули який зменшується із збільшенням температури. Відстань, на якій одна молекула відчуває іншу зменшується, отже звільняється місце для вільного пробігу. Середня довжина вільного пробігу визначається як відношення довжини шляху, пройденого молекулою, (у нашому випадку , до кількості зіткнень
Внутрішнє тертя (в’язкість) у газах. В'язкість або внутрішнє тертя — властивість текучих тіл (рідин і газів) чинити опір переміщенню однієї їх частини відносно іншої. Одиниця вимірювання — пуаз. молекул, а їх взаємним притяганням. Доказом цього є те, що із збільшенням температури, як відомо, обмін молекул зростає і тертя в газах зростає, а в рідинах спадає у зв'язку із послабленням міжмолекулярного притягання. характеризується коефіцієнтом пропорційності η між напруженням зсуву τ і градієнтом швидкості руху шарів динамічною в'язкістю або абсолютною в'язкістю. Одиниця вимірювання коефіцієнта динамічної в'язкості — Паc, Пуаз (0,1Па·с) .Кількісно коефіцієнт динамічної в'язкості дорівнює силі F, яку треба прикласти до одиниці площі зсувної поверхні шару S, щоб підтримати в цьому шарі ламінарну течію із сталою одиничною швидкістю відносного зсуву. в'язкість ν, що є відношенням коефіцієнта динамічної в'язкості до густини речовини зсуву (неньютонівські середовища; їхня в'язкість охоплює і так звану структурну в'язкість). Теплопровідність газів. Теплопровідність - це молекулярне переннесення енергії в суцільному середовищі,зумовлене градієнтом температури.Теплопровідність - один з видів теплопереносу поряд з конвективним теплообміном ітепловим випромінюванням. Розрізняють: згідно з яким густина теплового потоку пропорційна градієнту температури Jq(вектор) = - k grad T, деk- коеф. Теплопровідності ,Вт\(м*К); Коеф.теплопровідності - це фізичний параметр, який характеризує інтенсивність теплопровідності в речовині і чисельно дорівнює густині теплового потоку внаслідок теплопровідності при градієнті температури,що дорівнює одиниці.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.250 (0.008 с.) |

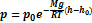
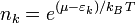 ,
,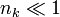 . Ця умова реалізується при високих
. Ця умова реалізується при високих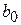
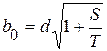 ,
,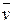 )
)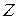 , що відбулися на цьому шляху
, що відбулися на цьому шляху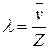 ,
,


