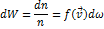Закон Авогадро. Рівняння Клайперона-Менделєєва.

Зако́н А́вогадро — однакові об'єми будь-яких газів при

однаковому тиску і температурі містять однакову кількість

молекул. Цей закон був відкритий італійським фізиком

Амедео Авогадро в 1811 році.

Наслідок закону Авогадро: однакові кількості молекул

різних газів при однаковій температурі і однаковому тиску

займають однакові об'єми. Так як 1 моль будь-яких газів

містить однакову кількість молекул — 6,02 • 10²³, це число

називають сталою Авогадро і позначають N_A.

Об'єм, який займає один моль будь-якого газу при нормальних

умовах, називається молярним об'ємом (позначається V_m).

Нормальними (скорочено н. у.) називаються такі умови, коли

температура дорівнює 0 °C, а тиск 1 ат., або 760 мм рт. ст.

Молярний об'єм усіх газів незалежно від їх маси

однаковий і дорівнює 22,4 дм³ (22,4 л).

Рівняння стáну ідеального газу(Клапейрона-Менделеєва) —

формула, що встановлює залежність між тиском, молярним

об'ємом і абсолютною температурою класичного ідеального

газу. Рівняння має вигляд:

Швидкості газових молекул та іх вимірювання.

Середня, середня квадратична та найбільш імовірна швидкості.

Явища молекулярної фізики визначаються у великій мірі

швидко­стями руху молекул. Швидкості газових молекул внаслідок

їхнього хаотичного руху відрізняються як за величиною, так і за

напрямом. Швидкість даної молекули газу в даний момент часу є

величина випадкова. У молеку­лярно-кінетичній теорії газів користуються

поняттями середньої <v>, середньої квадратичної <vкв. >

та найбільш імовірної (vн) швидкостей. Ці швидкості задаються

для рівноважних станів газу.

Се­редня (або середньоарифметична) швидкість визначається

рівнянням

Середня квад­ратична швидкість визначається з рівняння

За цією формулою можна обчислити також швидкість броунівських

частинок. Звичайно, при цьому т₀ — маса броунівської частинки. Цьому

виразу можна надати більш зручного вигляду, помножив­ши чисельник

і знаменник під коренем на число Авогадро. Врахову­ючи, що kNA=R та

m0NA=M, <vкв>=кор.кв.(3RT/M). Середню квадратичну швидкість

називають ще тепловою. тепловий рух досить інтенсивний для молекул,

помітний для мікроскопічних частинок, які здійснюють броунівський рух,

і зовсім непомітний для тіл великої ма­си.

 

Функція розподілу молекул за швидкостями. Розподіл Максвелла.

У стані статистичної рівноваги в ідеальному газі, яка настає внаслідок

зіткнень молекул між собою, встановлюється розподіл мо­лекул за

швидкостями, що не змінюється з часом. Визначити, яким буде

цей розподіл — одна із задач статистичної фізики.

Величину f(v) називають функцією розподілу молекул за швид­костями,

або інакше, густиною ймовірності розподілу швидкісних то­чок молекул

у просторі швидкостей. Функція f(v) описує лише ймовірний розподіл

молекул за швид­костями і змінюється неперервно зі зміною v. Функція

розподілу може стосуватися довільної неперервно змінної випадкової

величини: швидкості, координати, імпульсу, моменту кількості руху,

енергії тощо.

Формулу Максвелла, що визначає відносну кількість молекул,

швидкості яких лежать у межах v I v+dv, запишемо так:

Розподіл Максвелла має фундаментальне значення для молеку­лярної

теорії газів. Загальну теорію статистичних властивостей фізичних

систем розвинули Больцман та Гіббс. Розподіл Максвелла — це

перший приклад статистичного закону в науці. Дж. Максвелл

усвідомив, що випадковий рух окремих моле­кул підпорядкований

певному статистичному закону. Крива розподілу Максвелла вказує

на те, що в газі найбільша ча­стина молекул рухається з швидкостями,

значення яких близькі до vн. У законі Максвелла функція розподілу

залежить від при­роди газу та його температури. Розподіл Максвелла

передбачає, що на молекули газу не діють зовнішні сили. Тому молекули

рівномірно розподілені в певному об’ємі. Фактично молекули газів

перебувають під дією поля тяжіння.