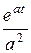Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории операционного исчисления
Элементы теории операционного исчисления ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Пусть функция f (t)обладает следующими свойствами: 10 f (t) Такие функции наз. изображаемыми по Лапласу или оригиналами. Запишем интеграл
где p = s + iq - комплексная переменная. При s Смысл преобразования – многим операциям над оригиналами соответствуют более простые операции над изображениями. Например, решение дифференциальных и интегральных уравнений может существенно упроститься. Нахождение изображений
Пр.1 Re p > 0 Пр.2 Re p > a = s 0
Свойство линейности. Т.к. интеграл от суммы функций равен сумме интегра-лов, то линейной комбинации оригиналов соответствует линейная комбина-ция изображений. С 1 f 1(t) + С 2 f 2(t) =: С 1 F 1(p) + С 2 F 2(p) Из формулы Эйлера eit = cos t + i sin t имеем соs t = ½(eit + e-it), sin t = ½ i (eit - e-it) и для оригиналов этих функций вычислим изображения Пр.3 f (t) = cos t = ½(eit + e-it) =: ½ [ Пр.4 f (t) = sin t = ½ i (eit - e-it) =: 1/2 i [ Пр.5 f (t) = t =: t 4 =: Теоремы подобия, смещения, запаздывания Теорема подобия. Дополнительное умножение аргумента t в оригинале на число а f (аt) =: Доказательство. f (аt) =: = Пр.6 sin at =: Теорема смещения. Переход в изображении от p к (p + z), где z комплексное число, причем Re (p + z) > s 0, приводит к дополнительному умножению оригинала на экспоненту e-zt F (p + z) =: e-zt f (t) (3) Доказательство. e-zt f (t) =: Пр.7 ezt sin at =: Теорема запаздывания. Уменьшение параметра t в оригинале на величину f (t - Доказательство. f (t - + Первый интеграл равен 0, т.к. f (t -
Пр.8
Поиск изображения по графику оригинала Пр.9 По данному графику оригинала найти изображение.
Построим аналитическое выражение для данной функции, на основе общего уравнения прямой, проходящей через две точки (t 1, y 1), (t 2, y 2)
Решение. Функцию на интервале [0, a] описывает разность двух единичных функций f (t) = Представим f (t) в виде суммы слагаемых двух типов f (t) = + С помощью соотношений Пр.8 совершим переход к искомому изображению F (t) =:
Таблица изображений
Свертка функций Опр. Сверткой функций f 1(t) и f 2(t) наз. интеграл от произведения этих функций Теорема о свертке Изображение свертки двух оригиналов равно произведению их изображений, т.е. если f 1(t) =: F 1(p), f 2(t) =: F 2(p), то
f 1(t)* f 2(t) =: F 1(p) F 2(p)(14)
Доказательство.Обе части формулы преобразований Лапласа F 1(p) =
Пр.18 Найти оригинал изображения F (p) = Решение 1. Имеем произведение изображений двух функций t и eat. Поэтому оригинал равен свертке этих функций f (t) = t* eat = J 1 = t =
Решение 2. Представим изображение в виде суммы простейших дробей: F (p) = p 2 | A + C = 0 A = - 1/ a 2 p 1 | - aA + B = 0 p 0 | - aB = 1 C = 1/ a 2 f (t) = -
Элементы теории операционного исчисления ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Пусть функция f (t)обладает следующими свойствами: 10 f (t) Такие функции наз. изображаемыми по Лапласу или оригиналами. Запишем интеграл
где p = s + iq - комплексная переменная. При s Смысл преобразования – многим операциям над оригиналами соответствуют более простые операции над изображениями. Например, решение дифференциальных и интегральных уравнений может существенно упроститься. Нахождение изображений
Пр.1 Re p > 0 Пр.2 Re p > a = s 0
Свойство линейности. Т.к. интеграл от суммы функций равен сумме интегра-лов, то линейной комбинации оригиналов соответствует линейная комбина-ция изображений. С 1 f 1(t) + С 2 f 2(t) =: С 1 F 1(p) + С 2 F 2(p) Из формулы Эйлера eit = cos t + i sin t имеем соs t = ½(eit + e-it), sin t = ½ i (eit - e-it) и для оригиналов этих функций вычислим изображения Пр.3 f (t) = cos t = ½(eit + e-it) =: ½ [ Пр.4 f (t) = sin t = ½ i (eit - e-it) =: 1/2 i [ Пр.5 f (t) = t =: t 4 =:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |
 0при t < 0; 20 | f (t)| < M
0при t < 0; 20 | f (t)| < M 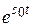 при t > 0, где М > 0, т.е. f (t) возрастает не быстрее некоторой экспоненты и s 0 – показатель роста функции; 30 На любом промежутке [ a, b ]положительной полуосивыполняются условия Дирихле – функция кусочно-непрерывна и имеет конечное число экстремумов и точек разрыва I рода.
при t > 0, где М > 0, т.е. f (t) возрастает не быстрее некоторой экспоненты и s 0 – показатель роста функции; 30 На любом промежутке [ a, b ]положительной полуосивыполняются условия Дирихле – функция кусочно-непрерывна и имеет конечное число экстремумов и точек разрыва I рода.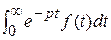 = F (p)(1)
= F (p)(1) и F (p)
и F (p) 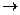 0. При указанных условиях он сходится и наз. интегралом Лапласа, а функция F (p) наз. изображением оригинала. Переход от f (t) к F (p) наз. преобразованием Лапласа и обозначается f (t) =: F (p) или F (p) =: f (t). Для значения f (t) в точке разрыва t 0 выбирают f (t 0) = ½ [ f (t 0 - 0) + f (t 0 + 0)]. При этих условиях между f (t) и F (p) существует взаимно – однозначное соответствие.
0. При указанных условиях он сходится и наз. интегралом Лапласа, а функция F (p) наз. изображением оригинала. Переход от f (t) к F (p) наз. преобразованием Лапласа и обозначается f (t) =: F (p) или F (p) =: f (t). Для значения f (t) в точке разрыва t 0 выбирают f (t 0) = ½ [ f (t 0 - 0) + f (t 0 + 0)]. При этих условиях между f (t) и F (p) существует взаимно – однозначное соответствие.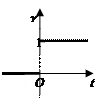 Вычислим изображение единичной функции и экспоненты
Вычислим изображение единичной функции и экспоненты ( t ) =
( t ) =  ,
, 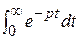 =
= 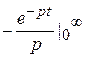 =
= 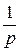 ,
, =
=  ,
, 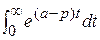 =
= 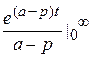 =
=  ,
,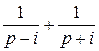 ] =
] = 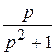
 ] =
] = 
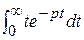 =
=  =
= 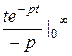 +
+ 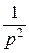 . f (t) = t 2 =:
. f (t) = t 2 =:  =
= 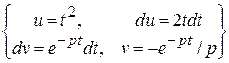 =
=  + +
+ + 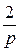
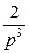 . Аналогично имеем t 3 =:
. Аналогично имеем t 3 =: 
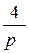
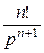 .
. R, a > 0 приводит в изображении к уменьшению в а раз параметра p и самого изображения,
R, a > 0 приводит в изображении к уменьшению в а раз параметра p и самого изображения, F (
F (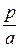 ). (2)
). (2)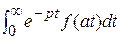 =
= 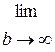
 =
=  =
=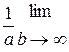
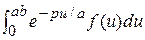 =
= 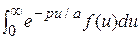 =
= 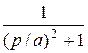 =
= 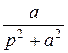 ; cos at =:
; cos at =: 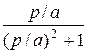 =
= 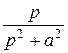
 =
= 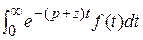 = F (p + z)
= F (p + z)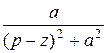 ; ezt cos at =:
; ezt cos at =: 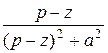
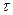 > 0 приводит к дополнительному умножению изображения на экспоненту
> 0 приводит к дополнительному умножению изображения на экспоненту 
 )
)  F (p) (4)
F (p) (4)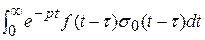 =
= 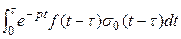 +
+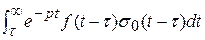
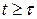
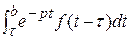 =
=  =
=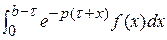 =
= 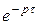
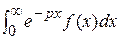 =
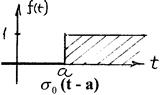
= 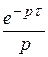 и (t – a)
и (t – a)  с учетом Пр. 5.
с учетом Пр. 5.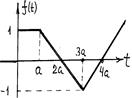
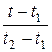 =
= 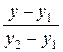 (5)
(5)
 и свойств единичной функции
и свойств единичной функции 
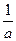 (t – 2 a). Для перехода от бесконечной прямой к отрезку на интервале [ a, 3 a ] умножим уравнение на разность
(t – 2 a). Для перехода от бесконечной прямой к отрезку на интервале [ a, 3 a ] умножим уравнение на разность 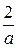 (t – 3 a)
(t – 3 a) 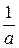
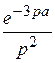 .
.
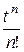
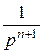

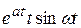
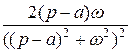
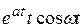
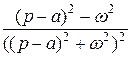
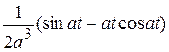
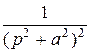
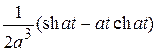

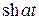


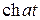
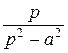
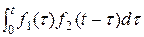
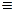 f 1(t)* f 2(t). Перестановка функций не меняет значения свертки.
f 1(t)* f 2(t). Перестановка функций не меняет значения свертки. умножим на F 2(p): F 1(p) F 2(p) =
умножим на F 2(p): F 1(p) F 2(p) = 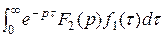 . По теореме запаздывания (4)
. По теореме запаздывания (4) 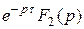 =: f 2(t -
=: f 2(t - 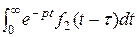 , где t >
, где t > 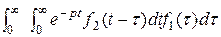 =
=  =:
=: 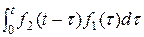 , т.к. при
, т.к. при 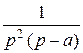 .
.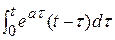 = t
= t  -
-  = J 1 - J 2,
= J 1 - J 2, -
- 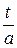 ; J 2 =
; J 2 = 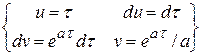 =
=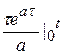 -
- 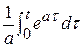 = t
= t  +
+  . Ответ f (t) =
. Ответ f (t) =  +
+  +
+ 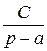 , тогда Ap (p – a) + B (p – a) + Cp 2 = 1
, тогда Ap (p – a) + B (p – a) + Cp 2 = 1 B = -1/ a По формулам № 1, 2, 3 получаем оригинал
B = -1/ a По формулам № 1, 2, 3 получаем оригинал