
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ministry of infrastructure of ukraineСодержание книги
Поиск на нашем сайте
MINISTRY OF INFRASTRUCTURE OF UKRAINE STATE SERVICE OF COMMUNICATION ODESSA NATIONAL ACADEMY OF TELECOMMUNICATIONS After A. S. POPOV ====================================================================== Department of physics of optical communications
PHYSICS of OPTICAL COMMUNICATION Module 2.3: Physics of optical communication PART 3: LABORATORY WORKS for bachelor training of educational area 0924 –“Telecommunications”
APPROVED by the Faculty Council Protocol № 4 from 19.11.2010 ODESSA 2012 UDK 538 (075.8) Publication plan 2012.
Writers: assoc. prof. Gorbachov V.E, instructor Kardashev K.D.
The following methodical guide is about section “Optics” of physics course for telecommunications technician. Six laboratory works allow students to learn basics of geometrical optics, wave optics and polarization phenomenon including birefringence. It contains sufficient theoretical information combined with detailed descriptions of applied equipment construction and measuring techniques for exploring properties of light. Recommended for students of TE-group, educational area 0924 –“Telecommunications”.
CONFIRMED at the Department session Protocol № 4 from 26.11.2010 INTRODUCTION The main goal of this laboratory course is advancing of theoretical knowledge on processes in devices of optical communication and familiarization of students with methods of investigation and measurement of different parameters of systems of optical communication. This laboratory works are made on a base of light emitted diode and photodiode. All laboratory works are provided in a frontal way, i.e. all group makes the same laboratory work at the same time. Appropriate homework must forego to work in a lab. The homework contains self-studying of theory and methodology of work accomplishment, preparation of protocol which includes experimental facility’s schematic drawing, equipment table's drawing, measurement table's drawing, a list of working formulae with description of all quantities which are in, list of test questions' answering. The allowance to performing of laboratory work will be had only those of students who have fulfilled homework and have positive result on express mini-quiz in a lab.
Content of the reports for all laboratory works has to be the following: 1) Number and title of laboratory work. 2) Goal of the work. 3) Laboratory-research facility's scheme. 4) Equipment table. 5) Equations for calculation with decryption of all quantities in. 6) Standard table of measurements for each measured quantity. It has to be checked and verified by an instructor. 7) Experimental data processing. 8) Standard form of result (confidence interval and relative error or a graphic result) 9) Conclusion 10) Date, name of a student. Besides this guide is recommended to use literature from bibliography given at the end of this guide. LIST OF LABORATORY WORKS
LABORATORY WORK № 8-5 1 Topic:STUDYING PHOTOCONDUCTIVITY OF HOMOGENEOUS SEMICONDUCTORS 2 Goal of the work: 1.1. Learning basic of internal photoelectric effect theory. 1.2. Acquaintance with the method of investigation of photoelectric properties of semiconductor. 1.3. Measurement of the lux-ampere characteristic in order to elucidate recombination mechanism of nonequilibrium charge carriers. Main concepts Photoconductivity is a phenomenon of change of electrical conductivity of crystals at light exposing due to the internal photoelectric effect. The internal photoelectric effect is a process of generation of charge carriers under the action of light, leading to increase of electrical conductivity.
The intrinsic photoconductivity is conductivity caused by light-induced transition of electrons from the valence band to the conductivity band. In this case, obviously, that the photon energy hν should satisfy the condition hν ³ Е g. Consequently, there is some boundary minimal frequency ν RB, at which the photoconductivity still observed. It is determined by the ratio hν RB= Е g. Corresponding boundary maximal wavelength λRB= c / ν RB called photoelectric threshold or red (long-wavelength) border of photoeffect. For example, for a semiconductor with a band gap Е g=2 eV we obtain boundary frequency ν RB= Е g / h =5ּ1014 s – 1, which corresponds to a long-wavelength border λRB=0,6ּ10 – 6 m. The impurity photoconductivity that appears during light-induced transitions types 2 and 3 (see Fig. 1) has a small probability, because at room temperature all impurity levels are already ionized. Detailed studying of the internal photoelectric effect shows that concentration of photocarriers at given intensity of light flux depends on its chemical composition. That is why each semiconductor has its own spectral characteristics (range of photosensitivity). In darkness semiconductor has any concentration of equilibrium electrons n 0 and holes р 0. During a light exposure the generation of excess (nonequilibrium) electron-hole pairs leads to increase in electrical conductivity of the semiconductor. Total conductivity, in the presence of nonequilibrium electrons Δ n and holes Δ р, can be written as:
Photoconductivity – is the excess conductivity, equal to the difference of conductivities of semiconductor at presence of illumination γ and in its absence γ0:
At continuous illumination by a white light (with equal intensity for all wavelengths), the steady-state concentration of nonequilibrium carriers Δ n and Δ р depend from the intensity of light.
where τ n и τ р – lifetime of electrons and holes respectively (time over which the carrier concentration decreases in e times after switching-off of illumination); h – quantum efficiency (number of electron-hole pairs, generated by one absorbed photon); α – absorption coefficient. In (3) quantum intensity of light Φ is equal an amount of photons, which fall on 1 m 2 of surface per 1 s. Then common light intensity I =Φ× hν, where hν – energy of one photon. From (2) and (3) we obtain dependence of stationary photoconductivity from light intensity, during continuous illumination:
If one of the terms in parentheses of equation (4) is significantly larger than the other (due to the difference in values of mobility or the lifetime of electron and hole), then, the photoconductivity is determined by the carriers of one sign, and called monopolar. In this case
Value τdetermined by conditions of recombination of charge carriers in the semiconductor and depends on many factors. In the simplest case it is a constant. Investigating the dependance of γPH from light intensity I (measuring the lux-ampere characteristics of the semiconductor) we can get some information about the conditions of recombination of charge carriers in a semiconductor. When semiconductor is illuminated with monochromatic light, it can be considered, that α=const and h=const. Linear dependence γPH from quantum intensity of light Φmeans, that the lifetime τ=const, i.e. it does not depend on the concentration of nonequilibrium carriers of charge. This is co-called linear recombination. If the dependence γPH from Φsublinear, i.e. γPH~ Ιа, where а <1, it means, that τ decreases with increasing light intensity, or, that is the and same, with increasing concentration of nonequilibrium carriers of charge. It is observed at high intensities of illumination.
On a Fig. 2 represented plot of photoconductivity versus quantum intensity of light Φ. The phenomenon of photoconductivity in semiconductors is widely used for measuring parameters of semiconductor materials, as well as in engineering to create a light-sensitive devices - photoresistors.
Data processing For representation of the result of direct measurements of quantity x: 1) Obtain the sequence of measured values x 1, x 2, x 3, ..., xN and write result of these n measurements in a second column of Table of measurements. In a first column of Table of measurements write an ordinal number of measurement. 2) Calculate the average value of measurand:
3) Find an abmodality of each measurement and write result in a third column of Table of measurements:
4) Square each abmodality in a fourth column of Table of measurements and summarize them:
5) Find a statistical absolute error D x ST of measurements from Student’s equation:
where a – confidence probability; N – total number of measurements; t a; N – Student’s coefficient. 6) If it is not identified an absolute instrumental error D x INST on measuring tool, it is necessary to find a device absolute error of measurements from accuracy class b of electrical measuring instrument:
where х max – grid limit. 7) Find a total absolute error of measurements
8) Calculate relative error of measurements:
9) Final result of direct measurements should be represented by a confidence interval and relative error:
For representation of the result of indirect measuring of quantity y it is necessary: 1) Calculate the average value of measurand < y > by formula from average values of known quantities < a >, < b >, < c >, for example:
2) Calculate relative error of measurand d y from relative errors of known quantities d a, d b, d c by formula that should be gained accordingly to this example:
where D a, D b, D c – absolute errors of known quantities; < a >, < b >, < c > – its average values. 3) Find an absolute error of measurand
4) Final result of indirect measuring should be represented by a confidence interval and relative error:
5 Description of laboratory research facility and methodology of measurements The experimental laboratory-research facility consists of semiconductor sample connected to a digital multimeter (set as Ohm-meter) and illuminator (see scheme in the protocol below). The sample is situated in front of the illuminator. Intensity of illumination of the sample is changed by changing the distance between sample and the illuminator lamp. LABORATORY WORK № 6- 9 1 Topic:STUDYING OF LIGHT-EMITTING DIODE 2 Goal of the work: Studying of transformation of an electrical energy into the light by light-emitting diode and measuring of its electric and light characteristics. Main concepts P-N junction P-n junction usually appears in internal part of a crystal conductor where type of dopant changes from acceptor to donor and, related with this, type of conductivity, from hole to electron. If there is no contact between semiconductors of p- and n- types then theirs Fermi levels are situated on a different heights: in p- type - closer to the valence band, and in n-type - close to the conductivity band (work function of electron from the p-region always
is greater than the work function from the n-region). When the contact appears (Fig. 14a) exchange of charge takes place in a result of which Fermi level becomes align. In the near-contact area appears depletion region which is depleted by the majority carriers: by electrons – from the side of the electron semiconductor, by holes – from the side of the holes semiconductor. Ions of impurities of this level create positive volume charge in the n-region and negative - in the p-region. Between n- and p- regions establishes built-in potential difference Δφ BI which resists to the movement of majority carriers. That’s why, to pass the p-n region, majority carriers must overcome the potential barrier e· Δφ BI. If we short-circuit some of the ends of two regions of the p-n junction then there will be no current in the circuit. It means that at the equilibrium, total current, created by the movement of majority and minority carriers through the contact junction, will be equal to zero. Connection of the external voltage of the direct polarity (forward bias) to the contact (plus – to p-semiconductor, minus – to n-semiconductor) leads to decreasing of the potential barrier (Fig. 14a b). Number of majority carriers, which are able to penetrate through the p-n junction increases, flux of minority carries stays the same. Current flows in the forward direction through the junction. If we apply to the junction reverse bias (Fig. 14c) then the external field of the reverse polarity sums with the internal field of the depletion region. Meanwhile for the diffusion current of the majority carriers appears great resistance. Through the contact flows the current of the reverse direction, which is in many times less than the forward direction current. Transition of minority carriers will have been finished at some value of reverse bias voltage. The reverse current, created only by the minority carriers, gets its saturation. LED properties In optical communication devices as a light source are used light-emitting diodes (LED), working in a mode of spontaneous emission (light-emitting diode) or in a stimulated emission mode (laser). Let’s consider the principle of work of such diode. Phenomenon of light emission during the flow of current is called the electroluminescence, and during the direct current flow through the p-n junction - injection electroluminescence. On the Fig. 15a shown the schematic division of the electroluminescence into elementary acts: injection of minority carriers (electrons in p-region and holes in n-region), transfer of carriers and its capture by recombination centers and radiative and non-radiative recombination.
On the Fig. 15b it’s shown the band diagram of p-n junction with the forward bias. When the forward bias voltage U is applied the potential barrier height EPB decreases by the value e·U, and diffusion currents begin to flow (electrons – to p-region and holes – to n-region (injection)). Injected charge carriers, which are minority and non-equilibrium ones, recombine non-radiative or with the emission of a photon with the correspondent energy. Part of a radiative recombination should be sufficiently great in LED. Current-Voltage characteristic (CVC) of LED ILED=f(U) has the appearance which is typical for a diode (Fig 16) and can be characterized by a cutoff voltage UCUT and residual resistance RRES. Cutoff voltage is received by an extrapolation of a linear section of a CVC to the current zero. Its value is close to the value of p-n junction built-in potential. Residual resistance RRES is determined as a cotangent of the slope angle of the linear section of a CVC.
Light characteristic of LED Ф=f(I) is the dependence of a power of emission Ф on the current I. Usually this characteristic is sublinear for small currents and linear for big ones. On small currents channels of non-radiative recombination play a big role and on big currents some of these channels become saturated and it leads to increasing of LED effectiveness. 4 Data processing (Same as in lab № 8.5) Test questions 1. How does the p-n junction appear and when does it conduct the current and when does not? 2. How does the electric energy transform into the light one in the LED? What is injection and radiative recombination? 3. What are the quantum and the energy efficiency? 4. What parameters can be defined from CVC? 5. How do the LED light properties depend on the current? Content of the report Laboratory work № 6-9 Ι. Homework. (answer on control questions from p.26) … ΙΙ. Laboratory work № 6-9 implementation protocol. 1) Topic: LABORATORY WORK № 6 – 10 Goal of the work Studying the photoelectric effect in a p-n junction and measuring of dark and light current-voltage characteristics. Main concepts 3.1 P-N junction ( see work 6-9 ) Photodiode properties
Photovoltaic effect consists in appearing of a photo-emf in a valve (i.e. rectifying) contact while it’s illuminated. The lowest frequency f0 (the highest wavelength λ 0 ) at which the photoelectric effect still possible called the photoelectric effect red border. It can be determined for given semiconductor from the condition: hf0 = Eg, that means that energy of photons hf0 must be not less than the forbidden energy gap width. On the Fig. 19 (curve 1) represented current-voltage characteristic of non-illuminated p-n junction. It can be described by such equation:
here IS – saturation current of non-illuminated p-n junction, k – Boltzman constant, e – elementary charge, T – temperature in Kelvins, U – external applied voltage.
Now let’s p-n junction be illuminated by light with energy of photons not less then forbidden gap width of the semiconductor. The internal photoelectric effect will lead to generation of electron-hole pairs, concentration of which will decrease with increasing of distance from illuminated surface. Electrons and holes will move to the junction, where they will be separated. Majority carriers of the region will be held by internal built-in electric field. Accelerated minority carriers will freely path through p-n junction, and create photocurrent IPHOTO, which flows in the reverse direction (from n- to p - region). If the circuit is open, then on the borders of p-n junction appears volume charge that opposes to further migration of charge carriers. This volume charge produces photo-emf U0 with polarity reverse to polarity of built-in potential. Potential barrier of depletion region decreases (Fig. 18b). That leads to appearance of leakage current IL flowing in the reverse direction. The photo-emf will be increased until the photocurrent will be compensated by increasing current of majority carriers. If we connect to p-n junction load resistance RLOAD (Fig. 20), than, in obtained circuit will flow a current I which can be represented as: I = IPHOTO - IL (47) Leakage current IL can be calculated by formula (46) for non-illuminated p-n junction when an external forward bias voltage ULOAD = I×RLOAD is applied:
Let’s consider the critical modes of operation of such photocell. 1.Short-circuit mode appears if RLOAD = 0. Then ULOAD = 0, IL = 0 and short circuit current ISC is equal to photocurrent IPHOTO which is proportional to light intensity Ф: ISC = IPHOTO; IPHOTO ~ Ф (48) 2.Open-circuit mode will take place if RLOAD = ¥. The open-circuit voltage VOC = UPHOTO, total current I = 0 and IPHOTO = IL. Equation (46) gives
from where we get
where UPHOTO – is a photo EMF generated in the photocell.
Thus, valve photocells allow to transform radiant energy directly into electric one. That is why they also called the photogalvanic elements and used as sources of EMF in the solar cell batteries. The current-voltage characteristic of illuminated p-n junction shown on the Fig.19 (curve2). Segment OA (U = 0) refers to short-circuit current (RLOAD = 0), segment OB (I = 0) – to open-circuit voltage (RLOAD =∞). Changing external load from 0 to ∞ we’ll get segment AB, which is a current-voltage characteristic of p-n junction in a photogalvanic mode at constant light intensity Ф. Segment BC characterize work of the photocell at forward bias voltage, segment AD – at reverse bias (photodiode mode). The CVCs will be displaced and change their shape under the change of light flux intensity. The photocell CVCs in a photogalvanic mode for different light intensities are shown on the figure 21. Straight line, drawn from the coordinate origin under the angle α (
Optimal load resistance
where Ф – light intensity in Watts, P – useful power, emitted on the load. 4 Data processing (Same as in lab № 8.5) Test questions 1. How the photoelectric effect occurs in a p-n junction? 2. What critical modes of operation of a photocell are possible? 3. How the short-circuit photocurrent depends on light intensity? 4. How the open-circuit photovoltage depends on light intensity? 5. What is photocell’s optimal load? 6. What is efficiency of the photocell? 7. What is photoelectric effect red border? 8. Describe the light and the dark CVCs of p-n junction. Content of the report Laboratory work № 6-10 Ι. Homework. (answer on control questions from p.34) … ΙΙ. Laboratory work № 6-10 implementation protocol. 1) Topic: BIBLIOGRAPHY 1. Викулин И.М., Горбачёв В.Э. Физика оптической связи: Метод. указания для самост. работы студентов по курсу физики. Одесса: Од. міська друкарня, 2000. 2. Кучерук І.М., Горбачук І.Т. Загальний курс фізики: Оптика. Квантова фізика. – К.: Техніка. 1999. - Т. III. 3. Матвеев А.Н. Оптика. — М.: Высшая школа, 1985. 4. Трофимова Т.Н. Курс физики. — М.: Высшая школа. 1985. 5. Зисман Г.А., Тодес О.М. Курс обшей физики. — М.: Наука, 1972. — Т. III. 6. Ландсберг Г.С. Оптика. — М.: Изд-во техн.-теорет. лит., 1957.
MINISTRY OF INFRASTRUCTURE OF UKRAINE
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.13 (0.008 с.) |


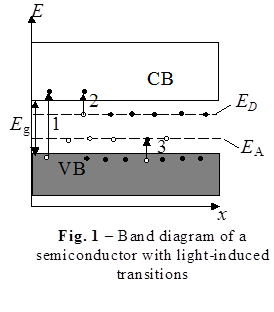 The primary process for the internal photoelectric effect is absorption of a photon with energy, sufficient for the transition of electron from valence band and donor level to conductivity band, as well as from valence band to acceptor level. On a Fig. 1 represented possible types of transitions, leading to changes in electrical conductivity. Transition 1 leads to generation of electron-hole pair, transitions 2 and 3 produce charge carriers of one sign from impurity atom (only electrons from donor impurity for transition 2, and only holes from acceptor impurity for 3).
The primary process for the internal photoelectric effect is absorption of a photon with energy, sufficient for the transition of electron from valence band and donor level to conductivity band, as well as from valence band to acceptor level. On a Fig. 1 represented possible types of transitions, leading to changes in electrical conductivity. Transition 1 leads to generation of electron-hole pair, transitions 2 and 3 produce charge carriers of one sign from impurity atom (only electrons from donor impurity for transition 2, and only holes from acceptor impurity for 3).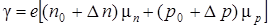
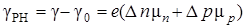
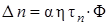 ;
;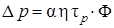 ,
,
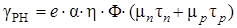
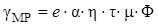
 Under certain conditions, dependence γPH from Φ can be superlinear. This means, that τ increases with increasing of light intensity, due to the complex processes of recharging of trapping centres in the semiconductor, leading to significant changes in the conditions of recombination of charge carriers.
Under certain conditions, dependence γPH from Φ can be superlinear. This means, that τ increases with increasing of light intensity, due to the complex processes of recharging of trapping centres in the semiconductor, leading to significant changes in the conditions of recombination of charge carriers.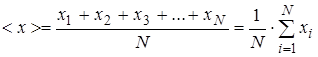 .
.
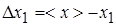 ;
; 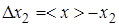 ;...;
;...; 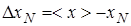 .
.
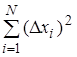
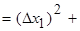
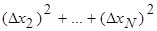 .
.
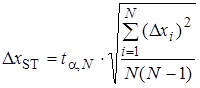 ,
,
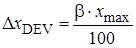 ,
,
 .
.
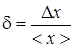 .
.
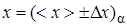 = (… ± …)0.95;
= (… ± …)0.95; 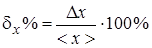 = … %.
= … %.
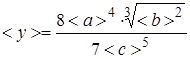 .
.
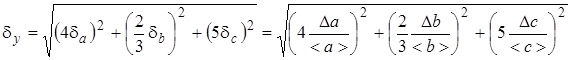 ,
,
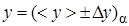 = (… ± …)0.95;
= (… ± …)0.95; 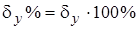 = … %
= … %
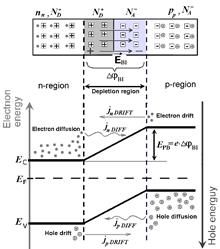
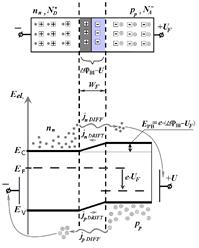
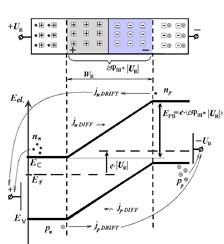
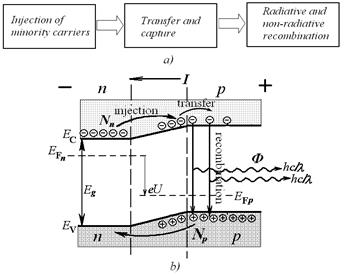 Figure 15 – Electrolumiscence in р-n-junction.
Figure 15 – Electrolumiscence in р-n-junction.
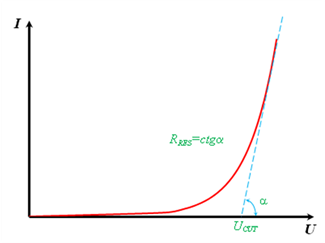 Figure 16 – CVC of LED
Figure 16 – CVC of LED
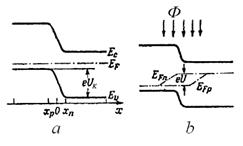 Figure 18 – Band diagram of non-illuminated (а) and illuminated (b) p-n junction.
Figure 18 – Band diagram of non-illuminated (а) and illuminated (b) p-n junction.
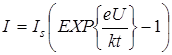 (46)
(46)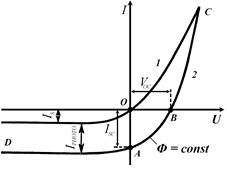 Figure 19 – CVC of the non-illuminated (curve 1) and illuminated (curve 2) р-n-junction.
Figure 19 – CVC of the non-illuminated (curve 1) and illuminated (curve 2) р-n-junction.
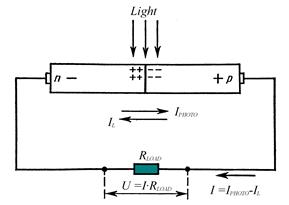 Figure 20 – Principle of operation of the photocell.
Figure 20 – Principle of operation of the photocell.
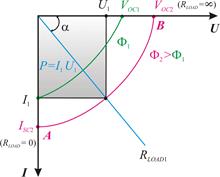 Figure 21 – photocells’ CVC at different light intensities.
Figure 21 – photocells’ CVC at different light intensities.
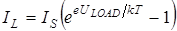 .
.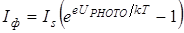 (49)
(49)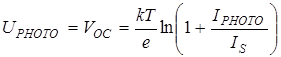 (50)
(50)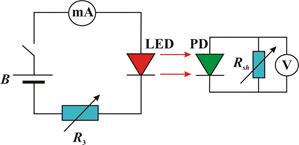 Figure 22 – Scheme of work 6-10 research facility
Figure 22 – Scheme of work 6-10 research facility
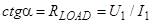 ), intersects the CVC at point, which X coordinate is equal to voltage drop on the load RLOAD, and Y coordinate – current in the external circuit (for example U 1 = I 1· RLOAD 1). Highlighted area (Fig.21) is proportional to power P, generated on the load RLOAD 1:
), intersects the CVC at point, which X coordinate is equal to voltage drop on the load RLOAD, and Y coordinate – current in the external circuit (for example U 1 = I 1· RLOAD 1). Highlighted area (Fig.21) is proportional to power P, generated on the load RLOAD 1: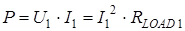 (51)
(51)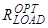 chosen in such way that this power will be maximal. Efficiency of the photogalvanic cell η determined as:
chosen in such way that this power will be maximal. Efficiency of the photogalvanic cell η determined as: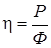 (52)
(52)


