
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра экспериментальной и теоретической физики
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Приборостроительный факультет Кафедра экспериментальной и теоретической физики ИЗУЧЕНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ Методическое указание к лабораторной работе №1 по дисциплине «Общая физика» Раздел «Механика. Молекулярная физика» Минск 2011 г. Введение
Физические законы устанавливаются и проверяются путем накопления и количественного сопоставления изменений экспериментальных данных, характеризующих изучаемое физическое явление. Таким образом, физика - это количественная наука, устанавливающая физические закономерности, которые выражаются в виде математических формул, связывающих между собой числовые значения физических параметров. Практически такая же методика измерений используется и в инженерных исследованиях и испытаниях. Поэтому целью физического практикума является выработка навыков правильного проведения измерений числовых значений различных физических параметров и умения оценивать погрешности и сопоставлять полученные данные с математическими формулами.
I Физические измерения и погрешности
Прежде всего, поясним, что вообще понимается под измерением. Измерением называется сравнение интересующей нас физической величины с соответствующим эталоном или измерительным прибором, проградуированным по эталону. По характеру проведения измерений их делят на прямые и косвенные. Под прямыми измерениями понимают такие измерения, при котором в ходе опыта непосредственно измеряется интересующая нас величина. Однако далеко не все величины можно определить путем прямого измерения. Например, плотность тела, определить непосредственным измерением весьма затруднительно. Но известно, что известно, что плотность определяется по формуле
где m и - v масса и объем, v=а.b.c, определяемый, например, геометрическими размерами образца. Измерение массы тела и его объема уже не представляет существенных трудностей, поэтому, измерив на опыте величины m и а,b,c, мы можем подставить их в (1) и рассчитать интересующее нас значение ρ. Такие измерения, при которых интересующая нас величина не измеряется непосредственно, а рассчитывается по некоторой формуле, на основе результатов прямых измерений, называются косвенными измерениями.
Погрешности измерений
Опыты показывают, что истинное значение любой физической величины определить невозможно, т.к. операции измерений производятся приборами, обладающими определенной предельной точностью, а сами измерения сопровождаются целым рядом объективных и субъективных ошибок или погрешностей. По характеру проявления погрешности можно условно разделить на следующие классы: приборные, систематические, случайные. Приборные погрешности. Если измерительный прибор исправен и отрегулирован, то на нем можно провести измерения с ограниченной точностью, определяемой типом прибора. Принято приборную погрешность стрелочного прибора считать равной половине наименьшего деления его шкалы. В приборах с цифровым отсчетом приборную ошибку приравнивают к величине одного наименьшего разряда шкалы прибора. Систематические погрешности - это ошибки, величина и знак которых постоянны для всей серии измерений, проведенных одним и тем же методом и с помощью одних и тех же измерительных приборов. При проведении измерений важен не только учет систематических ошибок, но необходимо также добиваться их исключения. Систематические погрешности условно разделяются на четыре группы: 1) погрешности, природа которых известна и их величина может быть достаточно точно определена. Такой ошибкой является, например, изменение измеряемой массы в воздухе, которая зависит от температуры, влажности, давления воздуха и т.д.; 2) погрешности, природа которых известна, но неизвестна сама величина погрешности. К таким погрешностям относятся ошибки, обусловленные измерительным прибором: неисправность самого прибора, несоответствие шкалы нулевому значению, классу точности данного прибора; 3) погрешности, о существовании которых можно не подозревать, но величина их зачастую может быть значительной. Такие ошибки возникают чаще всего при сложных измерениях. Простым примером такой ошибки является измерение плотности некоторого образца, содержащего внутри полости; 4) погрешности, обусловленные особенностями самого объекта измерения. Например, при измерении электропроводности металла из последнего берут отрезок проволоки. Погрешности могут возникнуть, если имеется какой-либо дефект в материале - трещина, утолщение проволоки или неоднородность, меняющие его сопротивление. Случайные погрешности - это ошибки, которые изменяются случайным образом по знаку и величине при идентичных условиях повторных измерений одного и того же параметра.
Отработка результатов косвенных измерений Метод частных производных Пусть интересующая нас величина y является некоторой функцией других величин xl, x2, x3 и т.д., так что
у = ƒ(xl, x2, x3...) (11)
причем величины xl, x2, x3... мы можем измерять путем прямых измерений. В этом случае мы для определения величин
Для определения полной абсолютной погрешности величины у необходимо выяснить, как изменяется эта величина при относительно небольших изменениях всех величин, от которых зависит величина у. Это можно сделать с помощью полного дифференциала. Интересующее нас изменение величины
где От бесконечно малых изменений величин у, xl, x2, x3... в (13) перейдем к конечным значениям их изменений
где ∆y - искомая полная погрешность величины
Под частной производной функции ƒ(x, y, z) по переменной X понимают величину:
т.е. это производная, которая вычисляется в предположении, что все переменные, кроме той, по которой берется производная, являются постоянными величинами. Например: пусть
После вычисления абсолютной ошибки ∆у по формуле (14) находят относительную ошибку как
Этот способ удобен в том случае, когда
Литература 1. Дж. Сквайрc. Практическая физика. - М: Мир, 1971. - 242 с. 2. Физический практикум. Механика и молекулярная физика. Под ред. В.И. Ивероновой. -М.: Наука, 1967. - 280 с. 3. Стандарт предприятия. СТП 01-01. 02-83. Отчет о 4. Дж. Тейлор. Введение в теорию ошибок. -М.: Мир. 1985. - 272 с. 5. Г.А. Зисман, О.М. Тодес Курс общей физики т. 1 – М. Наука, 1964. Киев, 1994. 6. Т.И. Трофимова Курс физики - М. ВШ, 1999. 7. Л.Д. Ландау, А.И. Китайгородский Молекулы книга 2. Физика для всех. – М. Наука, 1078. 8. Х. Кухлинг Справочник по физике - М. Мир, 1985 – перевод с немецкого 520 с. 9. И.В. Савельев Курс общей физики т. 1 Механика. Молекулярная физика - изд. 2. М. Наука, 1982. – 432 с. 10. И.В. Савельев Курс общей физики т.1 Механика. Колебания и волны, молекулярная физика - изд. 4. М. 1970 БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Приборостроительный факультет Кафедра экспериментальной и теоретической физики
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 69; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.75 (0.007 с.) |
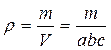 (1)
(1)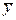
 и ∆ сначала измеряем все величины, от которых зависит у (xl, x2, x3...) по методике, изложенной в предыдущем параграфе. В результате чего определяем
и ∆ сначала измеряем все величины, от которых зависит у (xl, x2, x3...) по методике, изложенной в предыдущем параграфе. В результате чего определяем  , а также полные погрешности, в определении этих величин, которые обозначим как
, а также полные погрешности, в определении этих величин, которые обозначим как 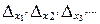 Наилучшее (среднее) значение косвенно определяемой величины у находится при подстановке в (6) наилучших (средних) значений
Наилучшее (среднее) значение косвенно определяемой величины у находится при подстановке в (6) наилучших (средних) значений
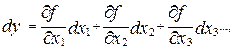 (13)
(13) - обозначают частные производные от функции f по соответствующим переменным. Эти частные производные вычисляются при наилучших (средних) значениях
- обозначают частные производные от функции f по соответствующим переменным. Эти частные производные вычисляются при наилучших (средних) значениях  (14)
(14)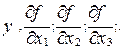 - значения соответствующих частных производных, вычисленных при наилучших (средних) значениях входящих в них величин.
- значения соответствующих частных производных, вычисленных при наилучших (средних) значениях входящих в них величин.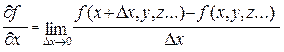 (15)
(15) . Тогда
. Тогда


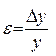 (16)
(16) представляет собой алгебраическую сумму.
представляет собой алгебраическую сумму.


