
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа в режиме калькулятораСодержание книги Поиск на нашем сайте
Ввод данных Ввод чисел с клавиатуры производится по правилам: - для отделения дробной части мантиссы числа применяется десятичная точка; - десятичный показатель числа записывается в виде целого числа после записи символа е; - между записью мантиссы числа и символом е не должно быть никаких символов, в т.ч. и символов пробела. Для записи промежуточных результатов в память ПК можно использовать имена переменных. Для этого применяется операция присваивания: <имя переменной> = <выражение> [;] Имена переменных могут содержать лишь буквы латинского алфавита или цифры и должны начинаться с буквы. Общее число символов в имени может достигать 19. Особенностью языка Matlab является то, что прописные и строчные буквы в именах различаются системой. Например, имена «а» и «А» обозначают разные переменные. Если выражение не заканчивается символом «;», результат его выполнения будет выведен в командное окно в виде: <имя переменной> = <результат> Ввод значений элементов матрицы осуществляется в квадратных скобках по строкам. Элементы строки отделяются друг от друга пробелом или запятой, а строки отделяются друг от друга знаком «;». Язык системы Matlab содержит встроенную арифметику комплексных чисел. Для обозначения мнимой единицы в Matlab зарезервировано два имени – i и j. Ввод с клавиатуры значения комплексного числа осуществляется следующим образом: <имя переменной> = <значение действительной части> + i [j] * < значение мнимой части> Переменные, зарезервированные системой Matlab: i, j – мнимая единица; pi – число p (3,141592653589793); inf – обозначение машинной бесконечности; NaN – обозначение неопределенного результата (например, типа 0/0 или inf/inf); ans – результат последней операции без знака присваивания. 3.2 Некоторые функции формирования матриц. Простейшие операции над матрицами zeros (m,n) – создает матрицу m´n с нулевыми элементами. ones (m,n) – создает матрицу m´n с единичными элементами. eye (m,n) – создает матрицу m´n с единичными элементами по главной диагонали и остальными нулевыми элементами. inv (A) – вычисляет матрицу, обратную матрице А. А ’ – вычисляет матрицу eig(A) – вычисляет массив собственных чисел матрицы А, т.е. корни характеристического полинома
[А В] – конкатенация (объединение) матриц А и В. Элемент матрицы А, находящийся на пересечении i-той строки и j-того столбца, обозначается A(i,j). Для доступа к i-той строке матрицы А следует указать: A[i,:]. Для доступа к j-тому столбцу матрицы А следует указать: A[:,j]. Для доступа к i-тому элементу вектора v следует указать v[i]. Задание Вычислите значение выражения где Для этого введите » A=[1 0 2 1; 0 2 1 0; 2 1 0 0; 1 0 0 0] A = 1 0 2 1 0 2 1 0 2 1 0 0 1 0 0 0 » B=[1 1 1 1; 2 1 -2 -1; 0 0 0 5] B = 1 1 1 1 2 1 -2 -1 0 0 0 5 » C=[1; 0; -2] C = -2 » E=eye(4) E = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 » (inv(A)-E)*B'*C % можно (A^-1-E)*B'*C ans = -10 -38 Получите матрицу F=[A BT]. Для этого введите: » F=[A B'] F = 1 0 2 1 1 2 0 0 2 1 0 1 1 0 2 1 0 0 1 -2 0 1 0 0 0 1 -1 5 Создайте вектор-строку v, состоящую из элементов третьей строки матрицы А. Для этого введите: » v=A(3,:) v = 2 1 0 0 Присвойте элементу А2,3 значение –5. Для этого введите: » A(2,3)=-5 A = 1 0 2 1 0 2 -5 0 2 1 0 0 1 0 0 0 Присвойте элементу v4значение элемента А2,3. Для этого введите: » v(4)=A(2,3) v = 2 1 0 -5 Операторы управления вычислительным процессом Оператор условного ветвления: if <логическое выражение1>, группа операторов1 elseif <логическое выражение2>, группа операторов2 else группа операторов3 End Оператор условия if... end вычисляет некоторое логическое выражение и выполняет соответствующую группу операторов в зависимости от значения этого выражения. Если <логическое выражение1> истинно, то выполняется группа операторов1, если же оно ложно проверяется <логическое выражение2>, если оно истинно, то выполняется группа операторов2, в противном же случае выполняется группа операторов3. Оператор elseif может многократно использоваться внутри оператора условия if... end. Оператор цикла с предпроверкой условия выхода: while <логическое выражение> группа операторов End Оператор цикла многократно выполняет группу операторов, пока <логическое выражение> истинно. Выход из while– цикла можно осуществить посредством вызова функции break. Оператор цикла с предопределенным числом повторений: for <переменная цикла>=<начальное значение>:<приращение >:<конечное значение> группа операторов End Оператор цикла for... end выполняет группу операторов заранее определенное число повторений. По умолчанию приращение равно единице. Но можно также задавать любое приращение, в том числе отрицательное или нецелое число. В качестве переменной цикла можно так же использовать и массивы, в этом случае цикл будет выполняться столько раз, сколько столбцов в матрице. При этом переменная цикла будет представлять из себя вектор-столбец соответствующий столбцу матрицы на каждом шаге цикла.
Задание Создайте и выведите на экран таблицу значений функции y=sin(x) при изменении х в диапазоне от 0 до 2p с шагом p/10. Для этого введите: »M=[ ]; » for x=0:pi/10:pi M=[M;[x sin(x)]]; End; M M = 0 0 0.3142 0.3090 0.6283 0.5878 0.9425 0.8090 1.2566 0.9511 1.5708 1.0000 1.8850 0.9511 2.1991 0.8090 2.5133 0.5878 2.8274 0.3090 3.1416 0.0000 Построение графиков Основной функцией, осуществляющей построение графиков на экране дисплея, является функция plot. Общая форма обращения к данной функции такова: plot (x1,y1,linespec1,x2,y2, linespec2,…) где xi – массив значений аргумента, а yi – массив значений функции, соответствующей i-тому графику. Параметры linespeci являются символьными (их указание необязательно). Параметр linespeci может содержать три специальных символа, определяющих тип линии, тип точки и цвет линии графика. Команда plot (y) строит график вектора у, используя в качестве аргумента порядковый номер элементов вектора. Если у – вектор комплексных чисел, то команда plot (y) отображает на комплексной плоскости элементы вектора, т. е. действует аналогично команде plot (real(y),imag(y)). Ниже приведены некоторые процедуры оформления графиков: grid – нанесение координатной сетки. title – заголовок графика. xlabel –название оси х. ylabel – название оси у. Чтобы создать несколько графических окон, необходимо воспользоваться командой figure, которая создает новое графическое окно, оставляя предыдущие. Чтобы разместить несколько графиков в одном окне, необходимо воспользоваться командой subplot. Обращение к этой процедуре должно предшествовать обращению к процедуре построения графика и выглядеть следующим образом: subplot (n,m,p) где число n указывает, на сколько частей делится поле графика по вертикали; m – по горизонтали; p – номер графического подокна, в котором будет строиться график. Подокна нумеруются слева направо, сверху вниз. Задание Выведите в одном графическом окне графики функций » t=0:0.01:10; » f1=exp(-t); f2=exp(-t/2); » plot(t,f1,t,f2); grid; xlabel('t'); ylabel('f1, f2'); » title('Графики функций f1=exp(-t) f2=exp(-t/2)') » figure; » subplot(2,1,1); plot(t,f1); grid; » xlabel('t'); ylabel('f1'); title(' График функции f1(t)=exp(-t))'); » subplot(2,1,2); plot(t,f2); grid; » xlabel('t'); ylabel('f2'); title(' График функции f2(t)=exp(-t/2))'); Выведите в третьем окне распределение элементов вектора » V=[-1-2i -1+2i 3i -3i 0.5 -1.5]; plot(V,'*');
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.102.123 (0.01 с.) |

 .
. .
.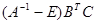 ,
, .
. и
и  при изменении t от 0 до 10, нанеся координатную сетку, подписав оси координат и дав название графику. А затем во втором графическом окне постройте графики указанных функций в разных подокнах. Для этого введите:
при изменении t от 0 до 10, нанеся координатную сетку, подписав оси координат и дав название графику. А затем во втором графическом окне постройте графики указанных функций в разных подокнах. Для этого введите: . Для этого введите:
. Для этого введите:


