
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм возведения в степень по модулю натурального числа.Содержание книги
Поиск на нашем сайте
Для выполнения шифрования по методу RSA приходится выполнять возведение в большую степень различных чисел, а результат приводить по модулю числа N, являющегося параметром метода и имеющего длину 512 и более бит. Уже для небольших a и e вычислить значение
выполняя сначала возведение в степень, а потом вычисляя остаток от деления Алгоритм быстрого возведения в степень основывается на идее замены прямого вычисления возведения в степень
где любое ti для
Например, если e = 13, то в двоичном представлении e = 11012, и 13 можно представить как результат вычисления Последнее число и есть e. Используя формулы (3), можно процедуру возведения в степень по модулю натурального числа N, записать в виде последовательности итераций:
где
Пример. Вычислить Решение. Переведем степень e=13 в двоичный вид. Для этого заполним следующую таблицу:
Таблица 1. Перевод десятичного числа e к двоичному представлению. Искомое двоичное разложение числа e будет во второй строке таблицы, записанное в обратном порядке справа налево.
Далее, составим таблицу вычисления с, заполняя следующую таблицу:
Таблица 2. Возведение а=5 в степень e=13 по модулю 19. В первой строке запишем цифры двоичное разложения числа 13. В первую ячейку второй строки поместим основание а =5. Далее каждое следующее значение с будем вычислять по формуле:
Например,
Приведем код на Паскале вычисления функции возведения в степень:
Function Rise(A,B,N:Integer):Integer; var B2:array[1..20] of byte; i,C,L:integer; Begin C:=B; i:= 1; While C > 0 do Begin B2[i]:= C Mod 2; C:= C div 2; i:= i + 1; End; L:= i - 1; i:= 1; D:= A; While i <L do Begin D:= (D * D) Mod N; If B2[L-i]= 1 Then D:=(D * A) Mod N; i:= i + 1; End; Rise:= D; End; Генерация простых чисел Для определения параметров RSA необходимо генерировать простые числа заданной длины. Согласно теореме Чебышева о распределении простых чисел число простых чисел на интервале [1; N ] равно примерно Function Generator(A as Integer, B as integer) As Integer Randomize t = Rnd() * (B - A) + A Generator = t End Function
1. Перебор делителей числа Т. Если число Т – составное, то найдется число k, меньшее Function Check_prime(T As Integer) As Boolean Dim k as integer Dim k As Integer Dim i As Integer Dim b As Boolean b = True k = Int(Sqr(T)) For i = 2 To k If T Mod i = 0 Then b = False Exit For End If Next i Test_prime = b End function 2. Тест Ферма. Согласно теореме Ферма, если число Т – простое, то для любого Если для произвольных различных k чисел a, меньших T, выполняется условие
К сожалению, полностью обратить теорему Ферма нельзя, т.к. существуют так называемые числа Кармайкла, для которых условие Ферма
3. Тест Миллера Рабина. Пусть R – произвольное натуральное число. Представим R–1 в виде 2s∙t, где t – нечетно. Пусть a < R–1 – натуральное число. Будем говорить, что число a отвергает простоту R, если выполнено одно из двух условий: а) R делится на a, б) Если найдется число а, отвергающее R, то R является детерминировано составным. Иначе, число a подтверждает гипотезу о простоте числа R (т.е усиливает вероятность того, что R является простым). Поэтому тест Миллера-Рабина является вероятностным.
Тест Миллера состоит из отдельных проверок для различных a < R–1 и выполняется следующим образом:
1. Выполняем разложение R–1 = 2s∙t, где t – нечетное число. 2. Выбираем случайное число a, 1 < a < R-1. Проверим, что R не делится на а нацело. Если делится, то R – составное. Иначе, продолжим тест. 3. Вычисляем 4. Последовательно выполняем итерацию Если раньше выполнится b = R–1, то число R – вероятно простое, иначе R – составное. 5. Повторим процедуру с новым а. После k циклов вероятность того, что R – составное, меньше 4-k, т.е. убывает очень быстро.
Разложение чисел на множители методом ρ-эвристики Полларда.
Этот метод факторизации натурального числа N был разработан известным криптографом Джоном Поллардом и является самым быстрым среди простых методов факторизации. Его идея состоит в том, что порождается случайная последовательность чисел {xi} (например, взяв x0=2, и продолжить вычисление по формуле
Замечание. Вычисление всевозможных разностей |xi - xj| требует хранения в памяти компьютера всех промежуточных значений xi, что отнимает много памяти, поэтому используется модификация Флойда, когда из всех xi, удовлетворяющих условию
Обоснование метода Полларда. Пусть p –делитель N. Среди членов последовательности {xi} рано или поздно попадутся числа xi и xj такие, что Оценка сходимости метода Полларда. Т.к. меньший делитель числа N меньше Рассмотрим пример. Пусть N=1387. Зададим рекуррентную последовательность чисел {xi} следующим соотношением:
Из таблицы видно, что уже на 7-м шаге был найден делитель N, равный 19.
Литература:
1. Ш.Т. Ишмухаметов. Методы факторизации натуральных чисел: учебное пособие, Казань, КФУ, 2011, 190 с. Электронная версия http://ksu.ru/f9/bibl/Monograph_ishm.pdf 2. Ишмухаметов Ш.Т. Технологии защиты информации в сети. Курс лекций. http://ksu.ru/f9/bin_files/metod_tzis!113.doc
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что вычисляет алгоритм Евклида? 2. Сколько строчек вычислений необходимо произвести в алгоритме Евклида? 3. Как производится заполнение столбцов x и y в расширенном алгоритме Евклида? 4. Какая алгоритмически сложная задача лежит в основе метода RSA? 5. Что такое простое число? Какие методы проверки простоты числа вы знаете? 6. Как генерируется параметры метода RSA? 7. Какие параметры в RSA вычисляются с помощью алгоритма Евклида? 8. Как производится процедура шифрования/расшифровки в методе RSA? 9. Какой длины должны быть простые числа p и q в методе RSA, чтобы обеспечить необходимый уровень надежности? 10. Каким образом, зная значение функции Эйлера и открытый ключ е, можно рассчитать закрытый параметр d? 11. Дайте определение односторонней функции. 12. Сколько итераций потребуется сделать в методе Полларда, если N ≈100 млн (108)? Лабораторная работа №2. Название работы. Разработка клиент-серверного приложения в Delphi.
Цель работы: Изучить современные средства создания клиент-серверных приложений в системе Delphi. Научиться практической работе по организации и решению задач информационной безопасности в сети. Задание на лабораторную работу. 1. Разработать, используя среду программирования Delphi клиент-серверное приложение для двустороннего обмена информацией между компьютерами в сети. Выполнить пробную передачу и прием данных. 2. Выработать секретный ключ по протоколу Диффи-Хелмана. 3. Провести аутентификацию пользователей по «слово-вызов».
Требования к выполнению задания. Клиентское приложение должно содержать форму, на которой содержатся поля для ввода IP-адреса компьютера – сервера, поле для ввода информации, передаваемое на сервер и поле для получения информации, возвращаемой с сервера. Приложение должен содержать кнопки Старт/Стоп для запуска и остановки сервера, поле для вывода информации, передаваемой с сервера, и поля для вывода информации, передаваемой клиентами. Приложение также должно содержать генератор ключей для протокола Диффи-Хелмана и вычисления секретного ключа. При сдаче необходимо установить клиентскую часть на один компьютер, а серверную часть приложения на другой компьютер, и продемонстрировать диалог обмена данными. Программно-аппаратные средства. Компьютерная лаборатория, состоящая из компьютеров, соединенных в локальную сеть, пакет Delphi 7 (Delphi 2005). Задание на лабораторную работу 1. Изучить теоретический материал по данной лабораторной работе. 2. Ознакомиться с указаниями по программированию в на языке Pascal в среде Delphi. 3. Разработать программный комплекс, представляющий собой клиент-серверное приложение в среде Delphi, решающее следующие задачи: · удаленную аутентификацию пользователей по алгоритму «Вызов-Ответ» с использованием хеш-функции MD5 или аналогичной. · генерацию общего секретного ключа по алгоритму Диффи-Хелмана. · шифрование данных по алгоритму RSA. 4. Выполнить пробное шифрование/расшифровку данных, передаваемых по сети в рамках компьютерного класса. Вставить в отчет полученные данные, описать методику выполнения задания. 5. Ответить на контрольные вопросы в конце задания. Теоретический материал.
Рассмотрим процедуры создания приложений для обмена сообщениями в сети по протоколам TCP/IP в среде Delphi.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

 (1)
(1) на N, становится невозможным. Между тем, если применить алгоритм, описанный в этом разделе, можно вычислять выражения (1), для достаточно больших чисел a, e, N, оставаясь в рамках обычных операций с целыми числами, заложенных в компьютере.
на N, становится невозможным. Между тем, если применить алгоритм, описанный в этом разделе, можно вычислять выражения (1), для достаточно больших чисел a, e, N, оставаясь в рамках обычных операций с целыми числами, заложенных в компьютере.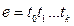 (2)
(2)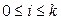 принадлежит
принадлежит  ,
,  . Зная вектор разрядов
. Зная вектор разрядов  , можно вычислить число e, применяя последовательные вычисления:
, можно вычислить число e, применяя последовательные вычисления: ,
,  (3)
(3)
 ,
,  .
.
 в зависимости от
в зависимости от  принимает либо значение a, если
принимает либо значение a, если  , либо 1, если
, либо 1, если  . Результат вычислений можно свести в таблицу
. Результат вычислений можно свести в таблицу 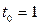







 .
.



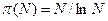 . Например, для N, равного 1 млн, число простых чисел в интервале от 1 до 106, равно примерно 50 тысяч. Для генерации простых чисел можно выбрать произвольное нечетное число T и проверить его на простоту с помощью одного из тестов, описанных ниже. Если T окажется составным, то надо заменить его на T+2 и проверить снова затем проверить T+4 и т.д. В среднем, через
. Например, для N, равного 1 млн, число простых чисел в интервале от 1 до 106, равно примерно 50 тысяч. Для генерации простых чисел можно выбрать произвольное нечетное число T и проверить его на простоту с помощью одного из тестов, описанных ниже. Если T окажется составным, то надо заменить его на T+2 и проверить снова затем проверить T+4 и т.д. В среднем, через  шагов простое число будет найдено. Для генерации числа из заданного интервала [A; B] в Visual Basic можно использовать следующий алгоритм:
шагов простое число будет найдено. Для генерации числа из заданного интервала [A; B] в Visual Basic можно использовать следующий алгоритм: , которое делит Т. Поэтому простейшим тестом на простоту является проверка делителей числа Т от 2 до
, которое делит Т. Поэтому простейшим тестом на простоту является проверка делителей числа Т от 2 до 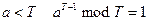 . На обращении этой теоремы основан следующий вероятностный тест:
. На обращении этой теоремы основан следующий вероятностный тест: , то с вероятностью, не меньшей, чем
, то с вероятностью, не меньшей, чем  , число a является простым.
, число a является простым.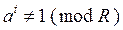 и для всех целых k,
и для всех целых k, 
 .
. . Если b равно 1, то R – вероятно простое число. Продолжаем тест со следующим a. Иначе, перейдем к следующему пункту.
. Если b равно 1, то R – вероятно простое число. Продолжаем тест со следующим a. Иначе, перейдем к следующему пункту. до тех пор, пока b не станет равным R–1, либо число итераций не превысит s-1, где s взято из пункта 1.
до тех пор, пока b не станет равным R–1, либо число итераций не превысит s-1, где s взято из пункта 1. ). Далее, вычисляются всевозможные разности
). Далее, вычисляются всевозможные разности  . Для каждой такой пары (xi, xj) находятся с помощью алгоритма Евклида наибольший общий делитель НОД(N, |xi - xj|)). Если будет найдена пара (xi, xj) со свойством НОД(N, |xi - xj|))>1, то этот НОД и даст искомый делитель числа N.
. Для каждой такой пары (xi, xj) находятся с помощью алгоритма Евклида наибольший общий делитель НОД(N, |xi - xj|)). Если будет найдена пара (xi, xj) со свойством НОД(N, |xi - xj|))>1, то этот НОД и даст искомый делитель числа N. вычитается только одно значение xj для j=2k (см.пример ниже).
вычитается только одно значение xj для j=2k (см.пример ниже). =
=  (это равенство записывается более кратко
(это равенство записывается более кратко  ). Это условие означает, что
). Это условие означает, что  для некоторого целого числа k. Т.к. p – делитель N, то для выбранной пары (xi, xj) НОД(N; |xi - xj|)= p.
для некоторого целого числа k. Т.к. p – делитель N, то для выбранной пары (xi, xj) НОД(N; |xi - xj|)= p. , то элементы последовательности
, то элементы последовательности 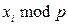 меньше
меньше  членов последовательности
членов последовательности  с вероятностью, большем чем 0,5, попадутся два одинаковых члена, т.е. найдутся i, j, удовлетворяющие условию
с вероятностью, большем чем 0,5, попадутся два одинаковых члена, т.е. найдутся i, j, удовлетворяющие условию  , членов последовательности.
, членов последовательности.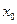 =2,
=2, 


