
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания к выполнению лабораторной работе.Содержание книги
Поиск на нашем сайте
Программа для реализация метода RSA должна содержать следующие необходимые процедуры, которые можно запускать отдельно: ¨ Реализацию расширенного алгоритма Евклида. ¨ Функцию быстрого возведения в степень по модулю заданного n. ¨ Функцию генерации простых чисел с проверкой простоты с помощью метода Миллера –Рабина. Простые числа, предназначенные для RSA, должны генерироваться с помощью датчика случайных чисел и находиться в интервале [1000; 2000]. Необходимо, чтобы каждое простое число p, генерируемое для RSA, удовлетворяло следующему условию: число p-1 должно содержать простой множитель больший 100. Последнее требование необходимо для противодействия разложению параметра n на простые сомножители (p-1)-методом Полларда. ¨ В второй части работы надо реализовать шифрованию/расшифровку текстов, вводимых с клавиатуры. Для шифрования текст разбивается на отдельные символы, заменяется кодом (например, ASCII) и шифруется путем возведения в степень ¨ В заключительной части необходимо реализовать взлом метода RSA, считая известным открытый ключ RSA. Для разложения числа на множители использовать ρ- метод Полларда. Выполнить контрольный взлом согласно номеру своего варианта (найти секретное слово, получив последовательность кодов ASCII после расшифровки). ВАРИАНТЫ ЗАДАНИЙ
Теоретический материал
Односторонняя (однонаправленная) функция (one way function) - это функция f, осуществляющая отображение X -> Y, где X и Y - произвольные множества, и удовлетворяющая следующим условиям:
1. Для каждого x из области определения функции 2. Задача нахождения прообраза
Задача разложения натурального числа N на простые множители (факторизация N) является задачей вычисления односторонней функции: зная сомножители p и q, нетрудно вычислить их произведение N=p • q, но обратная задача нахождения делителей p и q по известному N является сложной задачей, решение которой требует значительных вычислительных ресурсов. На вычислительной сложности решения этой задачи построен один из самых известных асимметричных методов криптографии – метод RSA. В 1977 году, когда создатели этого метода Ривест, Шамир и Адлеман объявили о новом методе криптографии, основанном на задаче факторизации, наиболее длинные числа, разложимые на множители, имели длину 40 десятичных цифр, что соответствует, примерно, 132-битовому двоичному числу (число 40 надо домножить на С тех пор был достигнут значительный прогресс в этой области. Число, предложенное создателями RSA, было разложено в 1994 году с помощью нового мощного метода факторизации – метода квадратичного решета (Quadratic Sieve Factoring), разработанного Карлом Померанцем и реализованного Аткинсом, Граффом, Ленстрой и Лейлендом. В работе участвовало около 600 добровольцев, задействовано в сети около 1700 компьютеров, которые работали в течение 7 месяцев. Параллельно с этим методом Джоном Поллардом, известным специалистом по криптографии и теории алгоритмов, был разработан еще более быстрый метод, получивший название метода решета числового поля (Generalizad Number Field Sieve - GNFS), который является наиболее быстрым методом и на сегодняшний день. Текущий рекорд, установленный немецкими исследователями, на июнь 2008 года, составляет 1000-бит. Это делает небезопасными ключи RSA длины 1024, которые являются на сегодняшний день, самыми распространенными.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.21.145 (0.006 с.) |

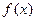 легко вычислить
легко вычислить 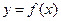 . Понятие «легко» обычно означает, что существует алгоритм, вычисляющий функцию f(x) за полиномиальное время от длины аргумента x.
. Понятие «легко» обычно означает, что существует алгоритм, вычисляющий функцию f(x) за полиномиальное время от длины аргумента x. для произвольного y, принадлежащего области значений функции
для произвольного y, принадлежащего области значений функции  существенно быстрее, чем алгоритм полного перебора.
существенно быстрее, чем алгоритм полного перебора. ). Создатели RSA предложили широкой публике расшифровать некую фразу английского языка. Для этого предварительно требовалось факторизовать 129-значное десятичное число N (длины 428 в битовом представлении), про которое было известно, что оно представимо в виде произведения двух простых сомножителей p и q, которые имели длину 65 и 64 десятичных знака.
). Создатели RSA предложили широкой публике расшифровать некую фразу английского языка. Для этого предварительно требовалось факторизовать 129-значное десятичное число N (длины 428 в битовом представлении), про которое было известно, что оно представимо в виде произведения двух простых сомножителей p и q, которые имели длину 65 и 64 десятичных знака.


