
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Детерминированное моделирование факторных системСодержание книги
Поиск на нашем сайте
Моделирование является основным приемом, в процессе которого осуществляется постепенный переход от исходной факторной системы к конечной, представляющей собой разложение результативного показателя по факторам. Моделирование основано на критериях выделения следующих факторов: причинности, достаточной специфичности, самостоятельности существования, учетной принадлежности. В экономическом анализе используются главным образом математические модели, описывающие изучаемое явление или процесс с помощью уравнений, неравенств, функций и других математических средств. Экономико-математическая модель должна быть адекватной действительности, отражать существенные стороны и связи изучаемого объекта. Различают два класса факторных систем: 1) детерминированные — построенные по цепочке действия прямых причинно-следственных связей; 2) стохастические (вероятностные), отражающие действие непосредственно не измеряемых факторов. В детерминированном моделировании факторных систем выделяют следующие виды конечных факторных систем: 1) аддитивная у = Σхi = х1 + х2 + х3 +…+ хn; 2) мультипликативная у = Пхi = х1 × х2 × х3 × … × хn; 3) кратная у = х1 / х2 ; у = Σхi / хi+1 ; у = Σ хi / Σ хj. Основные приемы моделирования: 1) метод удлинения факторных систем Пусть дана исходная факторная система у = а1 / а2. Если представить а1 в виде слагаемых, то получим новую факторную систему, то есть если а1 = а11 + а12 + а13 +…+ а1n, то у = (а11 + а12 + а13 +…+ а1n) / а2; 2) метод расширения факторных систем Пусть дана исходная факторная система у = а1 / а2 . Если и числитель и знаменатель умножить на одно и то же число, то получим новую факторную систему у =
3) метод сокращения факторных систем Пусть дана исходная факторная система у = а1 / а2 . Если и числитель и знаменатель разделить на одно и то же число, то получим новую факторную систему у = В основе детерминированного моделирования факторной системы лежит возможность построения тождественного преобразования для исходной формулы экономического показателя по теоретически предполагаемым прямым связям последнего с другими показателями-факторами. Детерминированное моделирование факторных служит основой для количественной оценки роли отдельных факторов в динамике изменения обобщающего показателя. Детерминированное моделирование факторных систем ограничено длиной факторного поля прямых связей. При недостаточном уровне знаний о природе прямых связей того или иного показателя хозяйственной деятельности часто необходим иной подход к познанию объективной действительности. Размах количественных изменений экономических показателей можно выяснить только стохастическим анализом массовых эмпирических данных. Способ цепных подстановок Цепные подстановки используются в экономическом анализе для исчисления влияния отдельных факторов на результативный показатель. Способ применяется при детерминированной связи в мультипликативной модели. Сущность этого способа заключается в постепенной и последовательной замене базисных величин частных показателей фактической величиной этих показателей. Затем определяется разниц между последующим и предыдущим вариантами расчетов. Подстановка — это условная величина, которая отвечает на вопрос каким было бы значение анализируемого показателя, если один из факторов изменяется, а все остальные остаются неизменными. При применении способа цепных подстановок должны соблюдаться следующие правила: 1) если на обобщающий показатель оказывают совместное влияние количественные и качественные факторы, то первоначально подстановкой определяют влияние количественных факторов, а затем — качественных. 2) если влияние какого-либо фактора на обобщающий показатель еще не определено, то его значение принимается в базисной величине, а если влияние уже установлено, то используют его фактическую величину. 3) плюс — это всегда увеличение, а минус — уменьшение, независимо от того носит ли изменение положительный или отрицательный характер. Существует обобщающий показатель вида у = а × в × с × d. В базисном периоде его значение будет уо = ао × во ×со × dо, а в текущем (анализируемом) у1 = а1 × в1 × с1 × d1. Изменение обобщающего показателя будет равно разности между фактическим и базисным значениями Δу = у1 – уо или (а1 × в1 × с1 × d1) – (ао × во × со × dо). При применении способа цепных подстановок последовательность определения влияния каждого фактора на обобщающий показатель будет следующая: уо = ао × во × со × dо I подстановка уа = а1 × во × со × dо II подстановка уb = а1 × в1 × со × dо III подстановка уc = а1 × в1 × с1 × dо IV подстановка уd = а1 × в1 ×*с1 × d1 Влияние каждого фактора: уа = уа – уо или (а1 ×во × со × dо) – (ао × во × со × dо) ув = ув – уа или (а1 ×в1 ×со × dо) – (а1 × во × со × dо) ус = уc – ув или (а1 × в1 × с1 × dо) – (а1 × в1 ×со × dо) уd = уd – ус или (а1 × в1 × с1 × d1) – (а1 × в1 × с1 × dо) Общая сумма отклонений фактического значения от базисного будет равно алгебраической сумме влияния факторов Δу = уа + ув + ус + уd Достоинства и недостатки способа цепных подстановок. Достоинства: — возможность безостановочного расчленения величины изменения сложного явления по факторам; — возможность объединения нескольких факторов или наоборот разукрупнять сложный фактор на ряд сомножителей; — расчеты не сложны и не связаны с использованием громоздких формул. Недостатки: — величины влияния отдельных факторов на результативный показатель зависят от последовательности подстановок. Если изменить порядок, то величина влияния каждого фактора изменится; — если при замене будет пропущен какой-либо фактор или допущена арифметическая ошибка при расчете его влияния, то общий результат окажется правильным, а величина влияния отдельных факторов — не верной.
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.209 (0.006 с.) |

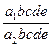 = (а1 / b) × (b / c) × (c / d) × (d / e) × (e / а2);
= (а1 / b) × (b / c) × (c / d) × (d / e) × (e / а2); =
=  .
.


