
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад виключення невигідних стратегійСодержание книги
Поиск на нашем сайте
Нехай дано платіжну матрицю. Знайдемо оцінки стратегій
нижню ціни гри. Оскільки вони різні
Оскільки гравець В мінімізує виграш гавця А, то для нього стратегії В1, В2, В3 заздалегідь невигідні в порівнянні із стратегією В5:
Розв'язавши гру 2х2, формуємо загальні оптимальні мішані стратегії:
Розв'язання ігор Можна показати, що довільна гра mxn має розв'язок, в якому число активних стратегій кожного гравця не перевищує Отже розв'язок гри 1) будується графічна модель гри; 2) виділяється ламана нижньої межі виграшу гравця А і знаходиться її максимум, що рівний ціні гри 3) визначається пара стратегій, які перетинаються в точці оптимуму. Це будуть активні стратегії гравця В. Якщо в точці оптимуму перетинаються більше двох кривих, то можна вибрати з них довільну пару; 4) параметри мішаних стратегій визначаються як для гри Розв'язок гри
Приклад розв'язку гри
Ломана B1NMB2 це нижня межа виграшу гравця А. Точка N є точкою оптимуму, тобто активними стратегіями гравця В є стратегії В1 та В2. Оптимальну стратегію гравця А знаходимо із системи рівнянь
Аналогічно знаходимо оптимальну стратегію гравця В із системи рівнянь
звідки Приклад розв'язку гри
Ломана А3NА1 це верхня межа програшу гравця В. Точка N є точкою оптимуму, тобто активними стратегіями гравця А є стратегії А3 та А1. Оптимальну стратегію гравця В знаходимо із системи рівнянь
Аналогічно знаходимо оптимальну стратегію гравця А із системи рівнянь
звідки
Зведення матричної гри Будемо вважати, що всі елементи платіжної матриці невід'ємні (якщо це не так, то можна до всіх елементів матриці додати деяке достатньо велике число L. При цьому ціна гри збільшиться на L, а розв'язок задачі не зміниться. Оскільки тоді
Враховуючи, що
Розділивши ліву і праву частини кожної з нерівностей (4.21) на
де Оскільки
Враховуючи, що гравець прагне максимізувати ціну гри, отримуємо умову на цільову функцію
Отже задача теорії ігор звелася до задачі лінійного програмування (4.24), (4.22), розв'язавши яку знаходимо ціну гри та оптимальну мішану стратегію гравця А:
Для побудови оптимальної мішаної стратегії гравця В за допомогою міркувань аналогічних наведеним приходимо до задачі лінійного програмування, яка двоїстою до задачі (4.24), (4.22):
Оптимальна стратегія гравця В знаходиться із співвідношення
При цьому
Системи масового обслуговування
Теорія масового обслуговування розробляє методи дослідження та отримує кількісні характеристики систем, на вхід яких в випадкові моменти часу поступають замовлення, тривалість обслуговування якого теж наперед невідома. Приклади: міська телефонна станція, ремонт несправного обладнання, приходи суден в порт і т.д.
Процес вибору замовлень з черги на обслуговування і розподіл їх по обслуговуючих пристроях характеризується дисципліною черги. Найчастіше зустрічається дисципліна першим прийшов-першим вийшов. Можливі інші варіанти дисципліни черги: останній прийшов-перший вийшов; випадковий вибір на обслуговування, пріоритетні системи масового обслуговування. Якщо вимоги із вищими пріоритетами в момент поступлення може перервати виконання замовлень із нижчими пріоритетами, то такі пріоритети називають абсолютними. Якщо таке переривання не допускається, то такі пріоритети наивають відносними. Вузол обслуговування може складатися з одного пристрою обслуговування (одно канальна система) або декількох пристроїв паралельного обслуговування (багатоканальна система), або послідовного багатоетапного.обслуговування (багатофазна система).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.112.15 (0.007 с.) |

 а потім верхню та
а потім верхню та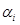

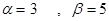 , то сідлової точки не існує. Порівнюючи стрічки А2 та А3, А3 та А4, виключаємо стратегії А2 та А4, як заздалегідь невигідні відносно стратегії А3.
, то сідлової точки не існує. Порівнюючи стрічки А2 та А3, А3 та А4, виключаємо стратегії А2 та А4, як заздалегідь невигідні відносно стратегії А3. .
.
 . Тобто ігри
. Тобто ігри  мають розв'язок, який містить не більше двох активних стратегій в кожного з гравців.
мають розв'язок, який містить не більше двох активних стратегій в кожного з гравців.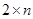 можна будувати наступним чином:
можна будувати наступним чином: ;
; .
. можна будувати подібно до попереднього. При цьому слід враховувати, що в цьому випадку шукається ламана верхньої межі прогашу гравця В і шукається її мінімальна точка.
можна будувати подібно до попереднього. При цьому слід враховувати, що в цьому випадку шукається ламана верхньої межі прогашу гравця В і шукається її мінімальна точка. , отже гра не має сідлової точки. Будуємо графічну модель
, отже гра не має сідлової точки. Будуємо графічну модель
 (4.16)
(4.16) розв'язавши яку отримуєм:
розв'язавши яку отримуєм: 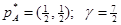
 (4.17)
(4.17)
 , отже гра не має сідлової точки. Стратегію А4 виключаємо як заздалегідь невигідну. Будуємо графічну модель
, отже гра не має сідлової точки. Стратегію А4 виключаємо як заздалегідь невигідну. Будуємо графічну модель
 (4.18)
(4.18)
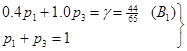 (4.19)
(4.19)
 до задачі лінійного програмування
до задачі лінійного програмування то
то  . Нехай гравець В застосовує свою чисту стратегію, а гравець А – свою оптимальну стратегію. Тоді середній виграш гравця А дорівнює
. Нехай гравець В застосовує свою чисту стратегію, а гравець А – свою оптимальну стратегію. Тоді середній виграш гравця А дорівнює (4.20)
(4.20)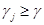 отримуємо
отримуємо (4.21)
(4.21) (4.22)
(4.22) .
. , то при діленні на
, то при діленні на 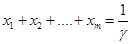 (4.23)
(4.23) (4.24)
(4.24) (4.25)
(4.25) (4.26)
(4.26) (4.27)
(4.27) (4.28)
(4.28) (4.29)
(4.29) (4.30)
(4.30) (4.31)
(4.31)



