Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип мінімаксу в парній грі з нульовою сумоюСодержание книги
Поиск на нашем сайте
Допускаємо, що гравці, які беруть участь в грі однаково розумні і кожен з них робить все для того, щоби максимізувати свій виграш. Якщо гравець А вибирає стратегію Аі, то розраховує на те, що гравець В вибере ту із стратегій, яка мінімізує виграш гравця А. Тому в кожній стрічці платіжної матриці гравець А знаходить свій мінімальний виграш
Знаючи свої мінімальні виграші
Оскільки гравець А розглядав найбільш несприятливі для себе варіанти, то встановлена ним величина Гравець В зацікавлений мінімізувати свій програш, або виграш гравця А. Тому він буде вибирати ту із стратегій, яка забезпечить мінімальний виграш гравця А серед його максимальних виграшів, тобто використає критерій мінімаксу.
де - максимальний виграш гравця А при виборі стратегії Вj. Значення
Існують ігри для яких нижня та верня ціни гри співпадають
Вони називаються іграми з сідловою точкою. Значення Приклад 2. Проаналізуємо задачу, наведену в прикладі 1.
Як видно з аналізу оптимальними стратегіями гравців є стратегії А3, В3.
Гра 2Х2 без сідлових точок
Нехай гравець А має m а гравець В – n стратегій. Враховуючи, що при відсутності сідлових точок нижня та верхня ціни гри не співпадають (
Стратегії гравців для яких імовірності використання в оптимальних мішаних стратегіях більші нуля, називаються активними. В основній теоремі теорії ігор доводиться, що всяка скінченна парна гра з нульовою сумою має хоча б один розв’язок в мішаних стратегіях. В найпростіших випадках цей розв’язок нескладно знайти аналітично з використанням простого графічного аналізу.
Крім того слід врахувати, що
покладаючи
Прирівнюючи (4.11) та (4.12), отримаємо рівняння відносно р1:
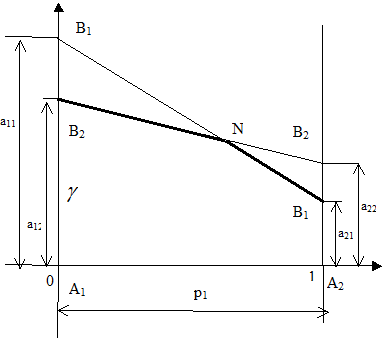
яке при конкретних значеннях коефіцієнтів платіжної матриці розв'язується елементарно. До рівняння (4.14) можна прийти також шляхом простого геометричного аналізу (див.рисунок). Для цього через кінці одиничного відрізка осі абсцис проведемо перпендикуляри, на яких будемо відкладати виграш гравця А при використанні чистих стратегій. Нехай лівому відрізку відповідає стратегія А1, а правому – А2. Відповідно на лівому перпендикулярі будуємо відрізки а11 та а12, а на правому – відрізки а21 та а22. Для побудови відрізка прямої, що відповідатиме результату гри при використанні другим гравцем стратегії В1, проведемо аналіз співвідношень (4.11), (4.13). Рівняння (4.11) визначає пряму, аргументом якої служить p1, а умова (4.13) зводить її до відрізка.
Побудуємо цей відрізок прямої за його крайніми точками. Зокрема в точці А1 p1=1 i Для знаходження оптимального значення
Щоб знайти точне числове значення величини . Оптимальна мішана стратегія гравця В знаходиться аналогічно. Однак відрізки, які будуть відкладатися на вертикалях В1 та В2 повинні відповідати вже результатам гри при цих стратегіях.Гравець В передбачає найбільш несприятливі для себе дії гравця A отримуючи верхню межу програшу – ламану A1NA2, ціну гри Слід відзначити, що розв'язок гри не завжди визначається точкою перетину ліній, що визначають результати гри для певних стратегій. На наступному малюнку показано, коли нижня границя виграшу гравця А співпадає з лінією В2В2.
Стратегія В1 для гравця В явно невигідна, тому гравець А аналізує лише його стратегію В2, вибираючи єдину оптимальну для себе стратегію А2. Отже дана гра має сідлову точку А2В2.Наступний малюнок представляє також випадок наявності сідлової точки, хоча точка перетину оціночних прямих існує. Тут оптимальною є стратегії А1В2
Спрощення ігор
Якщо платіжна матриця гри не містить сідлової точки, то складність розв'язання задачі можна значно знизити, якщо зменшити розмірність платіжної матриці шляхом викреслювання дублюючих та заздалегідь невигідних стратегій. Дублюючим стратегіям відповідають рівні стрічки (стовпчики) платіжної матриці. Якщо всі елементи i-ої стрічки (стовпчика) платіжної матриці не більші відповідних елементів стрічки (стовпчика) j, то стратегія Аі (Вj) називається заздалегідь невигідною.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.0.20 (0.006 с.) |

 (4.1)
(4.1) при використанні стратегії Аі,, гравець повинен зупинитися на тій із них, для якої
при використанні стратегії Аі,, гравець повинен зупинитися на тій із них, для якої  (4.2)
(4.2) називається нижньою ціною гри. Стратегія, яка забезпечує нижню ціну гри називається максимінною.
називається нижньою ціною гри. Стратегія, яка забезпечує нижню ціну гри називається максимінною. (4.3)
(4.3) (4.4)
(4.4) визначає верхню ціну гри, яка дає верхню оцінку програшу гравця В. Можна довести, що між нижньою та верхньою ціною гри завжди виконується співвідношення:
визначає верхню ціну гри, яка дає верхню оцінку програшу гравця В. Можна довести, що між нижньою та верхньою ціною гри завжди виконується співвідношення: (4.5)
(4.5) (4.6)
(4.6) в цих іграх визначає ціну гри, а стратегії, які її забезпечують будуть оптимальними. При відході одного гравця від своєї оптимальної стратегії та її дотриманні іншим гравцем, порушник отримує гірший результат ніж встановлена ціна гри.
в цих іграх визначає ціну гри, а стратегії, які її забезпечують будуть оптимальними. При відході одного гравця від своєї оптимальної стратегії та її дотриманні іншим гравцем, порушник отримує гірший результат ніж встановлена ціна гри.
 ), природнім є бажання гравця А збільшити свій виграш а гравця В – зменшити програш. Пошук компромісу приводить до використання складної стратегії, яка називається мішаною. Мішані стратегії гравців будемо позначати відповідно
), природнім є бажання гравця А збільшити свій виграш а гравця В – зменшити програш. Пошук компромісу приводить до використання складної стратегії, яка називається мішаною. Мішані стратегії гравців будемо позначати відповідно 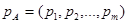 та
та  , де pi, qj – імовірності використання чистих стратегій Аі та Вj., причому
, де pi, qj – імовірності використання чистих стратегій Аі та Вj., причому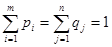 (4.7)
(4.7) Розглянемо найпростіший випадок – гру 2х2 без сідлової точки. Оскільки сідлової точки не існує, то всі стратегії гравців будуть активними. При використанні оптимальної мішаної стратегії гравцем А ціна результат гри буде рівний її ціні при виборі довільної стратегії гравцем В:
Розглянемо найпростіший випадок – гру 2х2 без сідлової точки. Оскільки сідлової точки не існує, то всі стратегії гравців будуть активними. При використанні оптимальної мішаної стратегії гравцем А ціна результат гри буде рівний її ціні при виборі довільної стратегії гравцем В: (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10) отримуємо
отримуємо (4.11)
(4.11) (4.12)
(4.12) (4.13)
(4.13) (4.14)
(4.14)
 . В точці А2 р1=0 і
. В точці А2 р1=0 і  . Оскільки пряма однозначно визначається двома точками, то сполучивши точки (0,а11) і (1,а21), отримаємо графік залежності результату гри при стратегії В1 від імовірності р1. Величина р1 будується на відрізку [0,1] як віддаль поточної точки до точки А2 (віддаль до одиниці). Аналогічно будується пряма для стратегії В2, що сполучає точки (0,а21) і (1,а22).
. Оскільки пряма однозначно визначається двома точками, то сполучивши точки (0,а11) і (1,а21), отримаємо графік залежності результату гри при стратегії В1 від імовірності р1. Величина р1 будується на відрізку [0,1] як віддаль поточної точки до точки А2 (віддаль до одиниці). Аналогічно будується пряма для стратегії В2, що сполучає точки (0,а21) і (1,а22). побудуємо нижню границю виграшу гравця І, тобто ломану B2NB1. Із цієї нижньої межі виграшів гравець І прагне вибрати максимальне значення, якому відповідає точка N. Ордината цієї точки рівна ціні гри а абсциса
побудуємо нижню границю виграшу гравця І, тобто ломану B2NB1. Із цієї нижньої межі виграшів гравець І прагне вибрати максимальне значення, якому відповідає точка N. Ордината цієї точки рівна ціні гри а абсциса 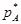 дозволяє знайти параметри оптимальної мішаної стратегії гравця І:
дозволяє знайти параметри оптимальної мішаної стратегії гравця І: (4.15)
(4.15)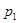 , потрібно розв'язати рівняння (4.14).
, потрібно розв'язати рівняння (4.14).
 та параметри
та параметри 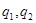 своєї оптимальної мішаної стратегії.
своєї оптимальної мішаної стратегії.